第一章相交线与平行线(培优)(含答案)
文档属性
| 名称 | 第一章相交线与平行线(培优)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 463.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-19 14:48:15 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章相交线与平行线(培优)
一、填空题
1.(2024九下·云南开学考)如图,在中,以点B为圆心,适当长度为半径画弧,分别交、于点P、Q,再分别以点P、Q为圆心,大于长度为半径画弧,两弧交于点M,连接交于点E,过点E做交于点D.若,,则的周长为 .
2.(2024九下·崇川期中)如图,,如果,那么的度数为 .
3.(2024七下·东兴月考) 如图,下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有 (填写所序号).
4.(2024七下·丰都县月考)如图,,平分,连接,交于点P.若,,则 .
5.(2024七下·越秀期中)如图,直线,,,则 °.
6.(2023七下·仙居期末)直线,将一块含角的直角三角板按如图方式放置,其中斜边与直线n交于点D.若,则的度数为 .
二、单选题
7.(2024八上·宁津期中)如图1,四边形是长方形纸带,其中,,将纸带沿折叠成图2,再沿折叠成图3,则图3中的度数是( )
A. B. C. D.
8.(2024九下·泸县月考)如图,直线,将一个含角的三角尺按如图所示的位置放置,若,则的度数为( )
A. B. C. D.
9.(2024七下·乳源期中)下列各图是由含或的直角三角板组合而成,其中利用内错角相等,画出的有( )
A.(1)(3) B.(2)(4)
C.(1)(2)(4) D.(2)(3)(4)
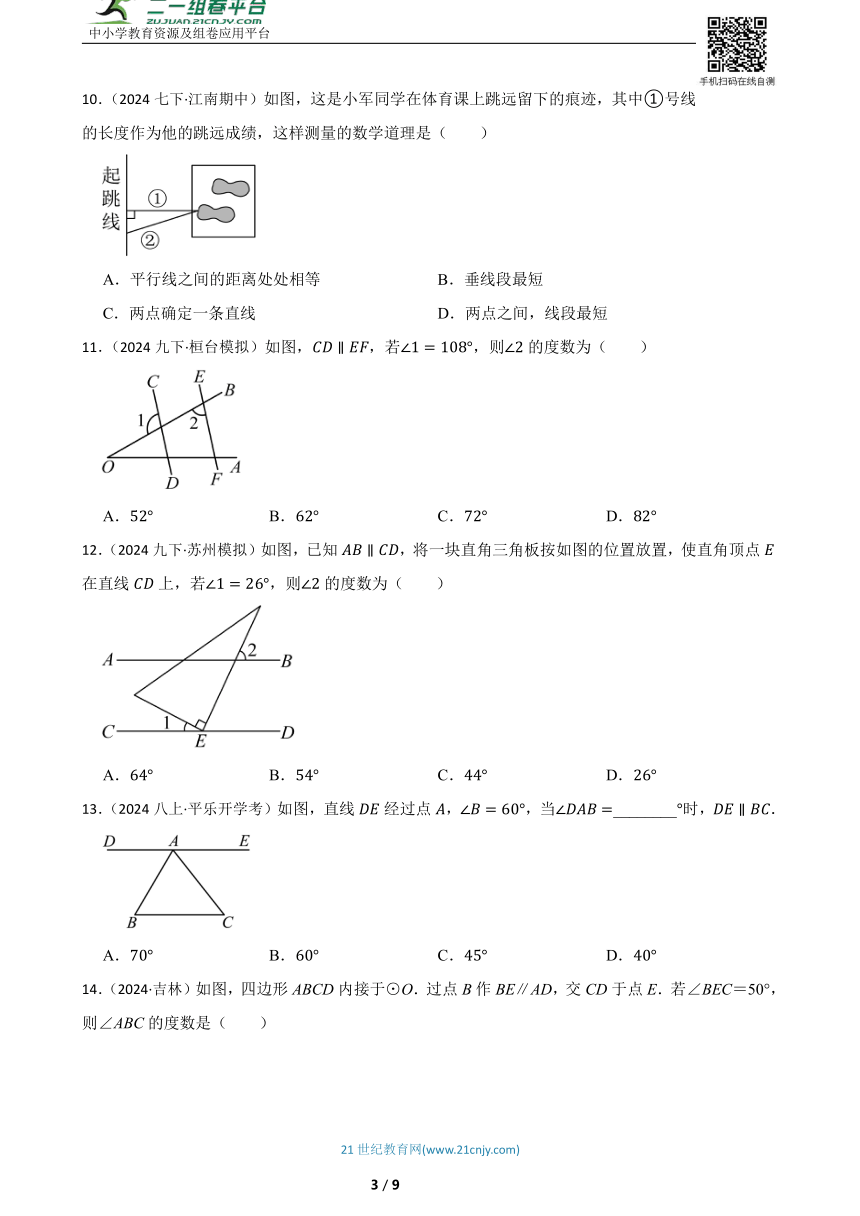
10.(2024七下·江南期中)如图,这是小军同学在体育课上跳远留下的痕迹,其中①号线的长度作为他的跳远成绩,这样测量的数学道理是( )
A.平行线之间的距离处处相等 B.垂线段最短
C.两点确定一条直线 D.两点之间,线段最短
11.(2024九下·桓台模拟)如图,,若,则的度数为( )
A. B. C. D.
12.(2024九下·苏州模拟)如图,已知,将一块直角三角板按如图的位置放置,使直角顶点在直线上,若,则的度数为( )
A. B. C. D.
13.(2024八上·平乐开学考)如图,直线经过点,,当________时,.
A. B. C. D.
14.(2024·吉林)如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
15.(2024七下·宜兴期中)如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A. B.
C. D.
16.(2024七下·襄都月考)下列图形满足“直线与直线相交,点M既在直线,又在直线上”的是( )
A. B.
C. D.
三、解答题
17.(2024七下·柳江期中)如图,,,,求的度数.请把下面的解答过程补充完整:
解:∵(已知),
∴______(______).
又∵(已知),
∴______(等量代换),
∴______(______),
∴______(______).
又∵(已知),
∴______.
18.(2024七下·思明期中)如图,直线与相交于点O,,若,求的度数.
19.如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOD=66°.求∠BOF的度数.
20.(2024七下·漳平期末)已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
四、计算题
21.(2023八上·墨玉期中)如图,在中,,交于点D,已知,平分,求的度数.
22.(2023七下·松原月考)如图,直线、相交于点O,,垂足为O,,求的度数.
23.(2024七下·林州期中)如图,,,, ,求:的度数.
请完成下面的推理和计算过程,并在括号内写明依据.
∵(已知)
∴ ① ( ② )
∵(已知)
∴ ③
∵(已知)
∴
∴ ④
∴ ⑤
∴( ⑥ )
∴ ⑦
∵
∴ ⑧° .
答案解析部分
1.【答案】9
【知识点】平行线的性质;等腰三角形的判定;角平分线的概念
2.【答案】
【知识点】对顶角及其性质;同旁内角的概念
3.【答案】①③④
【知识点】平行线的判定
4.【答案】
【知识点】平行线的判定与性质;三角形的外角性质
5.【答案】
【知识点】垂线的概念;平行公理及推论;平行线的性质;邻补角
6.【答案】
【知识点】角的运算;余角、补角及其性质;内错角的概念;同旁内角的概念
7.【答案】B
【知识点】平行线的性质;翻折变换(折叠问题)
8.【答案】C
【知识点】角的运算;平行线的性质;内错角的概念
9.【答案】B
【知识点】平行线的判定
10.【答案】B
【知识点】垂线段最短及其应用
11.【答案】C
【知识点】平行线的性质;邻补角;同位角的概念
12.【答案】A
【知识点】平行线的性质
13.【答案】B
【知识点】平行线的判定
14.【答案】C
【知识点】圆内接四边形的性质;两直线平行,同位角相等
15.【答案】C
【知识点】平行线的判定;对顶角及其性质
16.【答案】C
【知识点】相交线的相关概念
17.【答案】;两直线平行,同位角相等;;;内错角相等,两直线平行;;两直线平行,同旁内角互补;
【知识点】平行线的判定与性质
18.【答案】
【知识点】角的运算;垂线的概念;对顶角及其性质
19.【答案】解:∵∠AOD=66°,
∴∠BOC=∠AOD=66°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=33°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°-33°=57°.
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的概念
20.【答案】(1)证明:∵DF∥CA,
∴∠DFB=∠A,
又 ∵∠FDE=∠A,
∴∠DFB=∠FDE,
∴DE∥AB;
(2)解:设∠EDC=x°,
∵∠BFD=∠BDF=2∠EDC,
∴∠BFD=∠BDF=2x°,
由(1)可知∠DFB=∠FDE=2x°,
∴∠BDF+∠EDF+∠EDC=2x°+2x°+x°=180°,
∴x=36,
又∵DE∥AB,
∴∠B=∠EDC=36 °.
【知识点】角的运算;平行线的判定与性质
21.【答案】
【知识点】平行线的判定与性质;三角形内角和定理;直角三角形的性质
22.【答案】解:
【知识点】余角、补角及其性质;垂线的概念
23.【答案】① ②两直线平行,同位角相等 ③ ④ ⑤ ⑥内错角相等,两直线平行 ⑦ ⑧115°.
【知识点】平行线的判定与性质
21世纪教育网(www.21cnjy.com)
3 / 9
第一章相交线与平行线(培优)
一、填空题
1.(2024九下·云南开学考)如图,在中,以点B为圆心,适当长度为半径画弧,分别交、于点P、Q,再分别以点P、Q为圆心,大于长度为半径画弧,两弧交于点M,连接交于点E,过点E做交于点D.若,,则的周长为 .
2.(2024九下·崇川期中)如图,,如果,那么的度数为 .
3.(2024七下·东兴月考) 如图,下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有 (填写所序号).
4.(2024七下·丰都县月考)如图,,平分,连接,交于点P.若,,则 .
5.(2024七下·越秀期中)如图,直线,,,则 °.
6.(2023七下·仙居期末)直线,将一块含角的直角三角板按如图方式放置,其中斜边与直线n交于点D.若,则的度数为 .
二、单选题
7.(2024八上·宁津期中)如图1,四边形是长方形纸带,其中,,将纸带沿折叠成图2,再沿折叠成图3,则图3中的度数是( )
A. B. C. D.
8.(2024九下·泸县月考)如图,直线,将一个含角的三角尺按如图所示的位置放置,若,则的度数为( )
A. B. C. D.
9.(2024七下·乳源期中)下列各图是由含或的直角三角板组合而成,其中利用内错角相等,画出的有( )
A.(1)(3) B.(2)(4)
C.(1)(2)(4) D.(2)(3)(4)
10.(2024七下·江南期中)如图,这是小军同学在体育课上跳远留下的痕迹,其中①号线的长度作为他的跳远成绩,这样测量的数学道理是( )
A.平行线之间的距离处处相等 B.垂线段最短
C.两点确定一条直线 D.两点之间,线段最短
11.(2024九下·桓台模拟)如图,,若,则的度数为( )
A. B. C. D.
12.(2024九下·苏州模拟)如图,已知,将一块直角三角板按如图的位置放置,使直角顶点在直线上,若,则的度数为( )
A. B. C. D.
13.(2024八上·平乐开学考)如图,直线经过点,,当________时,.
A. B. C. D.
14.(2024·吉林)如图,四边形ABCD内接于⊙O.过点B作BE∥AD,交CD于点E.若∠BEC=50°,则∠ABC的度数是( )
A.50° B.100° C.130° D.150°
15.(2024七下·宜兴期中)如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A. B.
C. D.
16.(2024七下·襄都月考)下列图形满足“直线与直线相交,点M既在直线,又在直线上”的是( )
A. B.
C. D.
三、解答题
17.(2024七下·柳江期中)如图,,,,求的度数.请把下面的解答过程补充完整:
解:∵(已知),
∴______(______).
又∵(已知),
∴______(等量代换),
∴______(______),
∴______(______).
又∵(已知),
∴______.
18.(2024七下·思明期中)如图,直线与相交于点O,,若,求的度数.
19.如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥OE,且∠AOD=66°.求∠BOF的度数.
20.(2024七下·漳平期末)已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
四、计算题
21.(2023八上·墨玉期中)如图,在中,,交于点D,已知,平分,求的度数.
22.(2023七下·松原月考)如图,直线、相交于点O,,垂足为O,,求的度数.
23.(2024七下·林州期中)如图,,,, ,求:的度数.
请完成下面的推理和计算过程,并在括号内写明依据.
∵(已知)
∴ ① ( ② )
∵(已知)
∴ ③
∵(已知)
∴
∴ ④
∴ ⑤
∴( ⑥ )
∴ ⑦
∵
∴ ⑧° .
答案解析部分
1.【答案】9
【知识点】平行线的性质;等腰三角形的判定;角平分线的概念
2.【答案】
【知识点】对顶角及其性质;同旁内角的概念
3.【答案】①③④
【知识点】平行线的判定
4.【答案】
【知识点】平行线的判定与性质;三角形的外角性质
5.【答案】
【知识点】垂线的概念;平行公理及推论;平行线的性质;邻补角
6.【答案】
【知识点】角的运算;余角、补角及其性质;内错角的概念;同旁内角的概念
7.【答案】B
【知识点】平行线的性质;翻折变换(折叠问题)
8.【答案】C
【知识点】角的运算;平行线的性质;内错角的概念
9.【答案】B
【知识点】平行线的判定
10.【答案】B
【知识点】垂线段最短及其应用
11.【答案】C
【知识点】平行线的性质;邻补角;同位角的概念
12.【答案】A
【知识点】平行线的性质
13.【答案】B
【知识点】平行线的判定
14.【答案】C
【知识点】圆内接四边形的性质;两直线平行,同位角相等
15.【答案】C
【知识点】平行线的判定;对顶角及其性质
16.【答案】C
【知识点】相交线的相关概念
17.【答案】;两直线平行,同位角相等;;;内错角相等,两直线平行;;两直线平行,同旁内角互补;
【知识点】平行线的判定与性质
18.【答案】
【知识点】角的运算;垂线的概念;对顶角及其性质
19.【答案】解:∵∠AOD=66°,
∴∠BOC=∠AOD=66°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=33°,
∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°-33°=57°.
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的概念
20.【答案】(1)证明:∵DF∥CA,
∴∠DFB=∠A,
又 ∵∠FDE=∠A,
∴∠DFB=∠FDE,
∴DE∥AB;
(2)解:设∠EDC=x°,
∵∠BFD=∠BDF=2∠EDC,
∴∠BFD=∠BDF=2x°,
由(1)可知∠DFB=∠FDE=2x°,
∴∠BDF+∠EDF+∠EDC=2x°+2x°+x°=180°,
∴x=36,
又∵DE∥AB,
∴∠B=∠EDC=36 °.
【知识点】角的运算;平行线的判定与性质
21.【答案】
【知识点】平行线的判定与性质;三角形内角和定理;直角三角形的性质
22.【答案】解:
【知识点】余角、补角及其性质;垂线的概念
23.【答案】① ②两直线平行,同位角相等 ③ ④ ⑤ ⑥内错角相等,两直线平行 ⑦ ⑧115°.
【知识点】平行线的判定与性质
21世纪教育网(www.21cnjy.com)
3 / 9
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
