3.1 同底数幂的乘法 (1) 课件(共22张PPT)
文档属性
| 名称 | 3.1 同底数幂的乘法 (1) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-24 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
3.1 同底数幂的乘法(1)
浙教版七年级下册
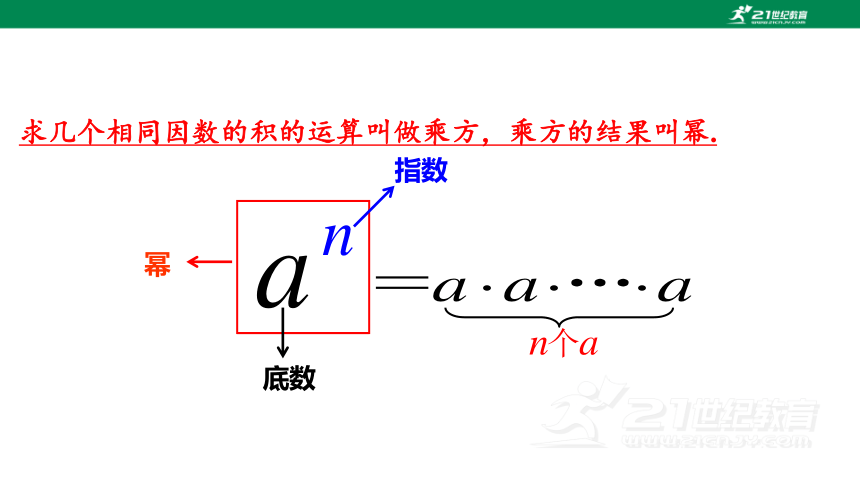
指数
底数
幂
求几个相同因数的积的运算叫做乘方,乘方的结果叫幂.
(1) 23×22 =( ) ×( )
= =2( )
(2) 4× 3 =( ) ×( )
= = ( )
(3) =( ) ×( )
= =5( )
=23+2
2×2×2
2×2
2×2×2×2×2
5
7
= 4+3
5×5×…×5
5×5×…×5
5×5×…×5
相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
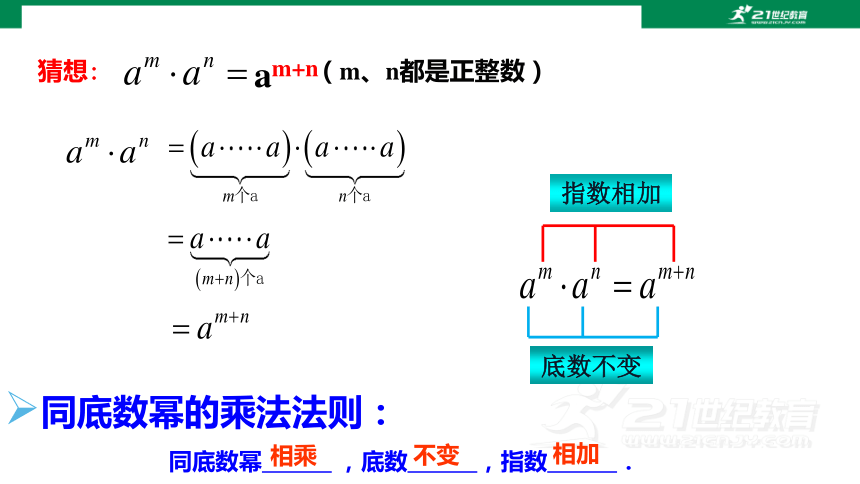
同底数幂相乘
底数不变
指数相加
同底数幂的乘法法则:
同底数幂 ,底数 ,指数 .
不变
相加
相乘
猜想: (m、n都是正整数)
am+n
猜想:
am+n+p (m、n、p都是正整数)
方法1
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
方法2
am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
am · an · ap =
例1 计算下列各式,结果用幂的形式表示
(1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3
(3) x3 · x5 (4) (a-b)2 (a-b)
运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果:
3 × 33 (2) (-3) 2 × (-3)3
(3) (-5) 2 × (-5)3 × 54 (4) (x+y) 3× (x+y)
解: (1) 3 × 33 = 31+3 = 34
(2) (-3) 2× (-3)3 = (-3) 2+3 = (-3)5 = -3 5
(-5) 2 × (-5)3 × 54
= (-5) 2 × (-5)3 × (-5)4 = (-5) 2+3+4 =(-5)9 = -5 9
(4) (x+y) 3× (x+y)= (x+y) 3+1= (x+y)4
例2 我国自主研发的“神威 太湖之光”超级计算机的实测运算速度达到每秒9.3亿亿次。如果按这个速度工作一整天,那么它能运算多少次?
解:
9.3亿亿次
=9.3×108×108次
24时
=24×3.6×103秒
(9.3×108×108 )×(24×3.6×103)
=(9.3×24×3.6)×(108×108×103)
= 803.52×1019
≈ 8.0×1021(次)
答:它一天约能运算8.0×1021次.
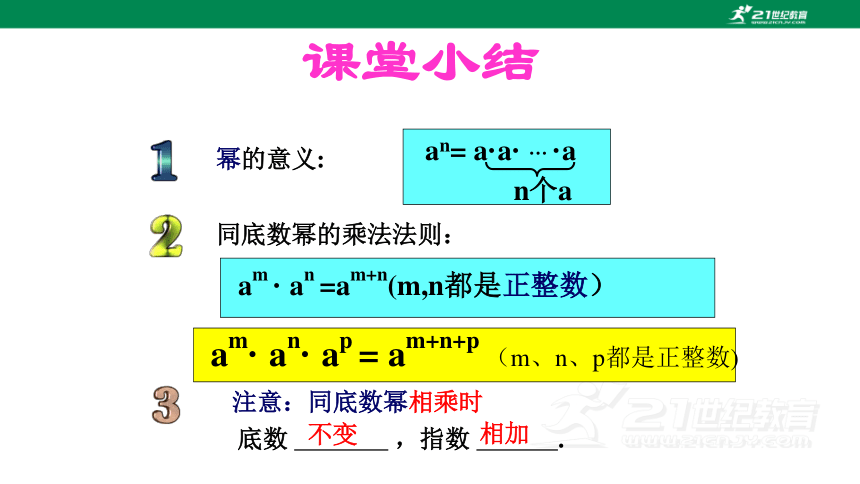
课堂小结
am · an =am+n(m,n都是正整数)
同底数幂的乘法法则:
底数 ,指数 .
不变
相加
幂的意义:
an= a·a· … ·a
n个a
注意:同底数幂相乘时
am· an· ap = am+n+p (m、n、p都是正整数)
1.判断(正确的打“√”, 错误的打“×”)
x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (3)x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5= x5 ( )
×
×
×
×
×
10
4
2x4
夯实基础,稳扎稳打
2、 计算:
(1) x2·x5; (2) a·a6;
(3)(-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解:(1)x2·x5 =x2+5 =x7.
(2)a·a6 =a1+6 =a7.
(3)(-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8
(4)xm·x3m+1=xm+3m+1=x4m+1.
3.计算:
(1)52×57; (2)7×73×72;
(3)-x2 x3; (4)(-c)3 (-c)m .
解:(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3)-x2 x3=-x2+3=-x5.
(4)(-c)3 (-c)m =(-c)3+m.
1-读
2-想
3-算
(-a)的立方
三个(-a)连乘的积
-a3
a的立方的相反数
三个a连乘的积的相反数
-a3
(-a)3
-a3
理解算式:
(-a)3=-a3
1-读
2-想
3-算
(-a)的4次幂
4个(-a)连乘的积
a4
a的4次幂的相反数
4个a连乘的积的相反数
-a4
(-a)4
-a4
理解算式:
(-a)4= -【-a4】
1-读
2-想
3-算
(-a)的n次幂
n个(-a)连乘的积
an
(-a) 的n次幂
n个(-a) 连乘的积
-an
(-a)n
n为偶数
n为奇数
an
-an
4.计算下列各式,结果用幂的形式表示.
连续递推,豁然开朗
=(-3)6=36.
=(-3)10=310.
=(-34)=-310.
=a4=-a8.
=25=7
5.计算
原式=-x2·x4·(-x3)=x2·x4·x3=x9.
原式=-(n-m)·(n-m)3·(n-m)4=-(n-m)1+3+4=-(n-m)8.
6、 已知:am=2, an=3.
求am+n .
解: am+n = am · an
=2 × 3=6
思维拓展,更上一层
∵am · an = am+n (m、n为正整数)
∴ am+n = am · an (m、n为正整数)
等式两边可以互换
7.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
3
36
22
×
=
33
32
×
×
=
23
25
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.1 同底数幂的乘法(1)
浙教版七年级下册
指数
底数
幂
求几个相同因数的积的运算叫做乘方,乘方的结果叫幂.
(1) 23×22 =( ) ×( )
= =2( )
(2) 4× 3 =( ) ×( )
= = ( )
(3) =( ) ×( )
= =5( )
=23+2
2×2×2
2×2
2×2×2×2×2
5
7
= 4+3
5×5×…×5
5×5×…×5
5×5×…×5
相乘结果的底数与原来底数相同,指数是原来两个幂的指数的和.
同底数幂相乘
底数不变
指数相加
同底数幂的乘法法则:
同底数幂 ,底数 ,指数 .
不变
相加
相乘
猜想: (m、n都是正整数)
am+n
猜想:
am+n+p (m、n、p都是正整数)
方法1
am·an·ap
=(am· an ) · ap
=am+n· ap
=am+n+p
方法2
am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
am · an · ap =
例1 计算下列各式,结果用幂的形式表示
(1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3
(3) x3 · x5 (4) (a-b)2 (a-b)
运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果:
3 × 33 (2) (-3) 2 × (-3)3
(3) (-5) 2 × (-5)3 × 54 (4) (x+y) 3× (x+y)
解: (1) 3 × 33 = 31+3 = 34
(2) (-3) 2× (-3)3 = (-3) 2+3 = (-3)5 = -3 5
(-5) 2 × (-5)3 × 54
= (-5) 2 × (-5)3 × (-5)4 = (-5) 2+3+4 =(-5)9 = -5 9
(4) (x+y) 3× (x+y)= (x+y) 3+1= (x+y)4
例2 我国自主研发的“神威 太湖之光”超级计算机的实测运算速度达到每秒9.3亿亿次。如果按这个速度工作一整天,那么它能运算多少次?
解:
9.3亿亿次
=9.3×108×108次
24时
=24×3.6×103秒
(9.3×108×108 )×(24×3.6×103)
=(9.3×24×3.6)×(108×108×103)
= 803.52×1019
≈ 8.0×1021(次)
答:它一天约能运算8.0×1021次.
课堂小结
am · an =am+n(m,n都是正整数)
同底数幂的乘法法则:
底数 ,指数 .
不变
相加
幂的意义:
an= a·a· … ·a
n个a
注意:同底数幂相乘时
am· an· ap = am+n+p (m、n、p都是正整数)
1.判断(正确的打“√”, 错误的打“×”)
x4·x6=x24 ( ) (2) x·x3=x3 ( )
(3) x4+x4=x8 ( ) (3)x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5= x5 ( )
×
×
×
×
×
10
4
2x4
夯实基础,稳扎稳打
2、 计算:
(1) x2·x5; (2) a·a6;
(3)(-2)×(-2)4×(-2)3; (4) xm·x3m+1.
解:(1)x2·x5 =x2+5 =x7.
(2)a·a6 =a1+6 =a7.
(3)(-2)×(-2)4×(-2)3=(-2)1+4+3=(-2)8
(4)xm·x3m+1=xm+3m+1=x4m+1.
3.计算:
(1)52×57; (2)7×73×72;
(3)-x2 x3; (4)(-c)3 (-c)m .
解:(1)52×57=52+7=59.
(2)7×73×72=71+3+2=76.
(3)-x2 x3=-x2+3=-x5.
(4)(-c)3 (-c)m =(-c)3+m.
1-读
2-想
3-算
(-a)的立方
三个(-a)连乘的积
-a3
a的立方的相反数
三个a连乘的积的相反数
-a3
(-a)3
-a3
理解算式:
(-a)3=-a3
1-读
2-想
3-算
(-a)的4次幂
4个(-a)连乘的积
a4
a的4次幂的相反数
4个a连乘的积的相反数
-a4
(-a)4
-a4
理解算式:
(-a)4= -【-a4】
1-读
2-想
3-算
(-a)的n次幂
n个(-a)连乘的积
an
(-a) 的n次幂
n个(-a) 连乘的积
-an
(-a)n
n为偶数
n为奇数
an
-an
4.计算下列各式,结果用幂的形式表示.
连续递推,豁然开朗
=(-3)6=36.
=(-3)10=310.
=(-34)=-310.
=a4=-a8.
=25=7
5.计算
原式=-x2·x4·(-x3)=x2·x4·x3=x9.
原式=-(n-m)·(n-m)3·(n-m)4=-(n-m)1+3+4=-(n-m)8.
6、 已知:am=2, an=3.
求am+n .
解: am+n = am · an
=2 × 3=6
思维拓展,更上一层
∵am · an = am+n (m、n为正整数)
∴ am+n = am · an (m、n为正整数)
等式两边可以互换
7.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
3
36
22
×
=
33
32
×
×
=
23
25
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
