1.1.1直线的相交 课件(共25张PPT)
文档属性
| 名称 | 1.1.1直线的相交 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-30 20:15:16 | ||
图片预览




文档简介
(共25张PPT)
第一章 直角三角形
1.1.1直线的相交
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
2.掌握对顶角的性质.发展推理能力,逐步掌握说理的基本方法.
1.了解相交线、对顶角的概念,能从图中辨认对顶角;
02
新知导入
这一组图片有什么共同特点?
有的线相交在一起.
03
新知探究
A
B
C
D
O
A
B
C
D
O
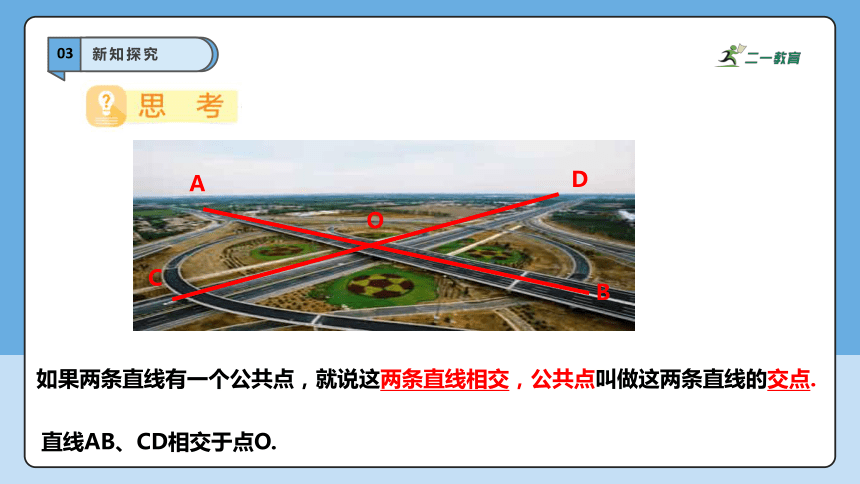
直线AB、CD相交于点O.
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点.
03
新知探究
1
2
3
4
A
B
C
D
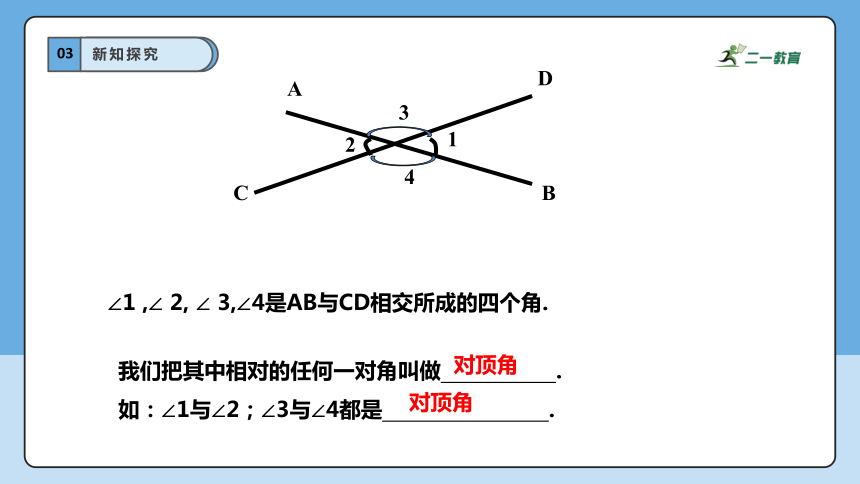
∠1 ,∠ 2, ∠ 3,∠4是AB与CD相交所成的四个角.
我们把其中相对的任何一对角叫做 .
如:∠1与∠2;∠3与∠4都是 .
对顶角
对顶角
03
新知讲解
对顶角的定义:∠1和∠2有一个公共顶点O,并且∠1的两边分别是∠2的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
对顶角的特点:
1.顶点相同.
2.角的两边互为反向延长线.
新课探究
例1
C
D
A
B
E
F
O
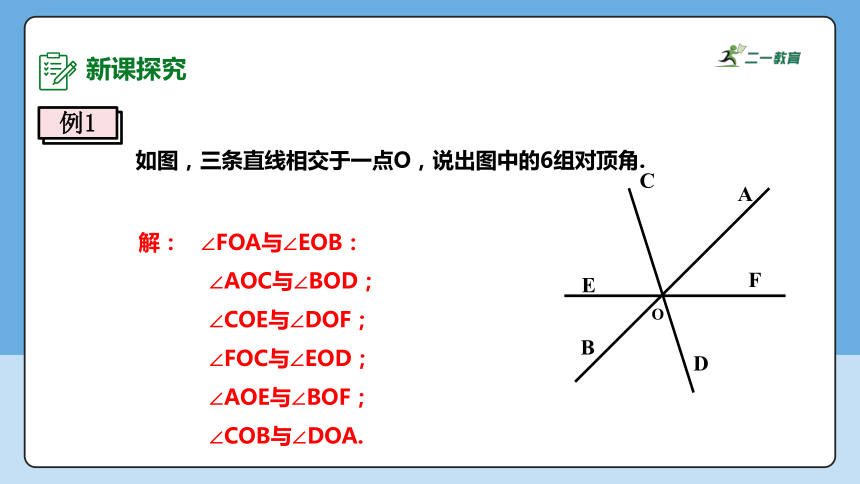
如图,三条直线相交于一点O,说出图中的6组对顶角.
解: ∠FOA与∠EOB:
∠AOC与∠BOD;
∠COE与∠DOF;
∠FOC与∠EOD;
∠AOE与∠BOF;
∠COB与∠DOA.
03
新知讲解
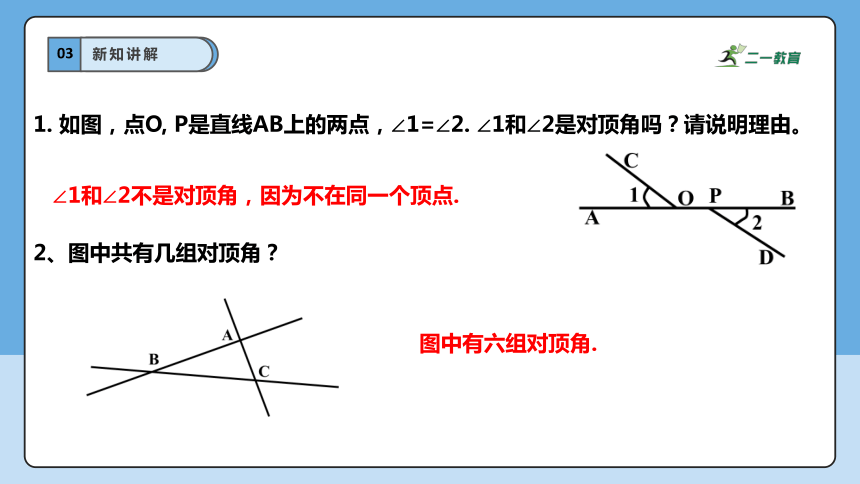
2、图中共有几组对顶角?
1. 如图,点O, P是直线AB上的两点,∠1=∠2. ∠1和∠2是对顶角吗?请说明理由。
∠1和∠2不是对顶角,因为不在同一个顶点.
图中有六组对顶角.
03
新知讲解
∠1 与∠3在数量上又有什么关系呢?
你是怎样得到的?
相等
03
新知讲解
∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180(邻补角定义)
∴∠1=∠3(等角的补角相等)
你能说出∠1=∠3的道理吗?
请你用数学语言写出这个过程.
对顶角的性质:
对顶角相等.
03
新知讲解
例2.如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=62°,求∠AOB的度数.
A
O
E
B
C
62°
解:∵∠DOE与∠COE互余(已知),
∴∠DOE+∠COE=90°(互余的意义),
∴∠DOE=90°-∠COE=90°-62°=28°,
又∵∠AOB与∠DOE是对顶角(已知),
∴∠AOB=∠DOE
∴∠AOB=28°.
03
新知讲解
1、对顶角的定义及判定条件.
2、对顶角的性质:对顶角相等.
(1)顶点相同,
(2)角的两边互为反向延长线.
提炼概念
03
新知讲解
04
课堂练习
【知识技能类作业】必做题:
1、下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D .
C
04
课堂练习
【知识技能类作业】选做题:
2.如图,直线AB、CD交EF于点G、H,∠2=∠3,∠1=70°,求∠4的度数。
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°-∠ = ( 的定义)
1
对顶角相等
已知
70°
∠2=∠3
70 °
等量代换
3
110 °
邻补角
04
课堂练习
【综合拓展类作业】
3. 已知直线AB、CD、EF相交于点O,∠1∶∠3=3∶1,
∠2=20°.
(1)图中的对顶角有哪几对?
(2)求∠DOE的度数.
解:(1)图中对顶角有:∠AOE与∠BOF,∠AOC与∠BOD,
∠EOC与∠DOF,∠EOB与∠AOF,∠COB与∠AOD,
∠COF与∠EOD,共6对对顶角.
(2)设∠3=x,则∠1=3x,
得3x+x+20=180,x=40,即∠3=40°,
∴∠DOE=180°-∠3=180°-40°=140°.
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1、如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC
=100°,则∠AOC是( )
A. 150° B. 130°
C. 100° D. 90°
B
06
作业布置
【知识技能类作业】选做题:
2.如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=65°,求∠AOB的度数.
A
O
E
B
C
65°
解:∵∠DOE与∠COE互余(已知),
∴∠DOE+∠COE=90°(互余的意义),
∴∠DOE=90°-∠COE=90°-65°=25°,
又∵∠AOB与∠DOE是对顶角(已知),
∴∠AOB=∠DOE
∴∠AOB=25°.
06
作业布置
【综合拓展类作业】
3. 平面上有9条直线,无任何3条交于一点,试问这9条
直线的位置关系如何,才使它们的交点恰是26个?
06
作业布置
【综合拓展类作业】
6.观察下列图形,寻找对顶角(不含平角).
图1
(1)如图(1)所示,图中共有____对对顶角;
(2)如图(2)所示,图中共有____对对顶角;
(3)如图(3)所示,图中共有____对对顶角;
2
6
12
06
作业布置
【综合拓展类作业】
(4)研究(1)~(3)小题中直线条数与对顶角的关系,若有n条直线相交于一点,则可形成__________对对顶角;
(5)若有180条直线相交于一点,则可形成_________对对顶角.
(n-1)n
32220
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.1.1直线的相交
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
2.掌握对顶角的性质.发展推理能力,逐步掌握说理的基本方法.
1.了解相交线、对顶角的概念,能从图中辨认对顶角;
02
新知导入
这一组图片有什么共同特点?
有的线相交在一起.
03
新知探究
A
B
C
D
O
A
B
C
D
O
直线AB、CD相交于点O.
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点.
03
新知探究
1
2
3
4
A
B
C
D
∠1 ,∠ 2, ∠ 3,∠4是AB与CD相交所成的四个角.
我们把其中相对的任何一对角叫做 .
如:∠1与∠2;∠3与∠4都是 .
对顶角
对顶角
03
新知讲解
对顶角的定义:∠1和∠2有一个公共顶点O,并且∠1的两边分别是∠2的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
对顶角的特点:
1.顶点相同.
2.角的两边互为反向延长线.
新课探究
例1
C
D
A
B
E
F
O
如图,三条直线相交于一点O,说出图中的6组对顶角.
解: ∠FOA与∠EOB:
∠AOC与∠BOD;
∠COE与∠DOF;
∠FOC与∠EOD;
∠AOE与∠BOF;
∠COB与∠DOA.
03
新知讲解
2、图中共有几组对顶角?
1. 如图,点O, P是直线AB上的两点,∠1=∠2. ∠1和∠2是对顶角吗?请说明理由。
∠1和∠2不是对顶角,因为不在同一个顶点.
图中有六组对顶角.
03
新知讲解
∠1 与∠3在数量上又有什么关系呢?
你是怎样得到的?
相等
03
新知讲解
∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180(邻补角定义)
∴∠1=∠3(等角的补角相等)
你能说出∠1=∠3的道理吗?
请你用数学语言写出这个过程.
对顶角的性质:
对顶角相等.
03
新知讲解
例2.如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=62°,求∠AOB的度数.
A
O
E
B
C
62°
解:∵∠DOE与∠COE互余(已知),
∴∠DOE+∠COE=90°(互余的意义),
∴∠DOE=90°-∠COE=90°-62°=28°,
又∵∠AOB与∠DOE是对顶角(已知),
∴∠AOB=∠DOE
∴∠AOB=28°.
03
新知讲解
1、对顶角的定义及判定条件.
2、对顶角的性质:对顶角相等.
(1)顶点相同,
(2)角的两边互为反向延长线.
提炼概念
03
新知讲解
04
课堂练习
【知识技能类作业】必做题:
1、下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D .
C
04
课堂练习
【知识技能类作业】选做题:
2.如图,直线AB、CD交EF于点G、H,∠2=∠3,∠1=70°,求∠4的度数。
解:∵∠2=∠ ( )
∠1=70 °( )
∴∠2= (等量代换)
又∵ (已知)
∴∠3= ( )
∴∠4=180°-∠ = ( 的定义)
1
对顶角相等
已知
70°
∠2=∠3
70 °
等量代换
3
110 °
邻补角
04
课堂练习
【综合拓展类作业】
3. 已知直线AB、CD、EF相交于点O,∠1∶∠3=3∶1,
∠2=20°.
(1)图中的对顶角有哪几对?
(2)求∠DOE的度数.
解:(1)图中对顶角有:∠AOE与∠BOF,∠AOC与∠BOD,
∠EOC与∠DOF,∠EOB与∠AOF,∠COB与∠AOD,
∠COF与∠EOD,共6对对顶角.
(2)设∠3=x,则∠1=3x,
得3x+x+20=180,x=40,即∠3=40°,
∴∠DOE=180°-∠3=180°-40°=140°.
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1、如图所示,直线AB、CD相交于点O,且∠AOD+∠BOC
=100°,则∠AOC是( )
A. 150° B. 130°
C. 100° D. 90°
B
06
作业布置
【知识技能类作业】选做题:
2.如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠COE=65°,求∠AOB的度数.
A
O
E
B
C
65°
解:∵∠DOE与∠COE互余(已知),
∴∠DOE+∠COE=90°(互余的意义),
∴∠DOE=90°-∠COE=90°-65°=25°,
又∵∠AOB与∠DOE是对顶角(已知),
∴∠AOB=∠DOE
∴∠AOB=25°.
06
作业布置
【综合拓展类作业】
3. 平面上有9条直线,无任何3条交于一点,试问这9条
直线的位置关系如何,才使它们的交点恰是26个?
06
作业布置
【综合拓展类作业】
6.观察下列图形,寻找对顶角(不含平角).
图1
(1)如图(1)所示,图中共有____对对顶角;
(2)如图(2)所示,图中共有____对对顶角;
(3)如图(3)所示,图中共有____对对顶角;
2
6
12
06
作业布置
【综合拓展类作业】
(4)研究(1)~(3)小题中直线条数与对顶角的关系,若有n条直线相交于一点,则可形成__________对对顶角;
(5)若有180条直线相交于一点,则可形成_________对对顶角.
(n-1)n
32220
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
