1.1.2 直线的相交 课件(共25张PPT)
文档属性
| 名称 | 1.1.2 直线的相交 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-31 00:00:00 | ||
图片预览



文档简介
(共25张PPT)
第一章 直角三角形
1.1.2直线的相交
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
2.掌握垂线的性质及垂线段的性质.
1.了解垂线、垂线段、点到直线的距离等概念;
02
新知导入
03
新知探究
α
a
b
b
b
b
b
)
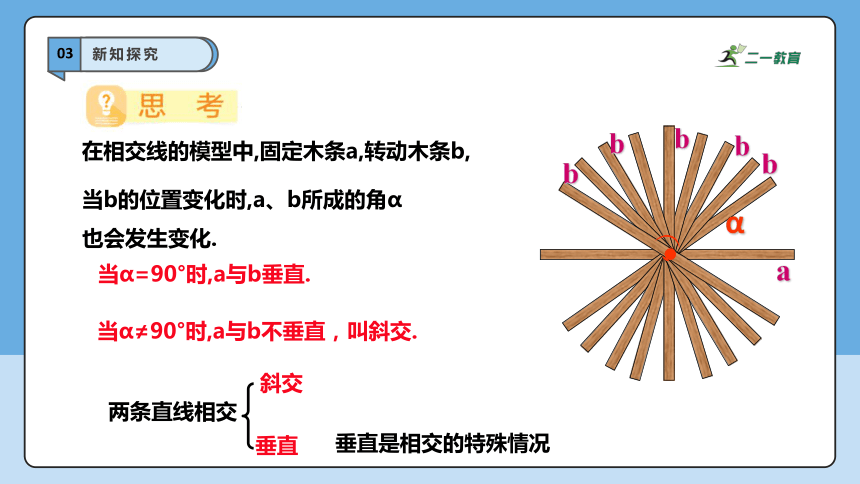
在相交线的模型中,固定木条a,转动木条b,
当α=90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
03
新知探究
03
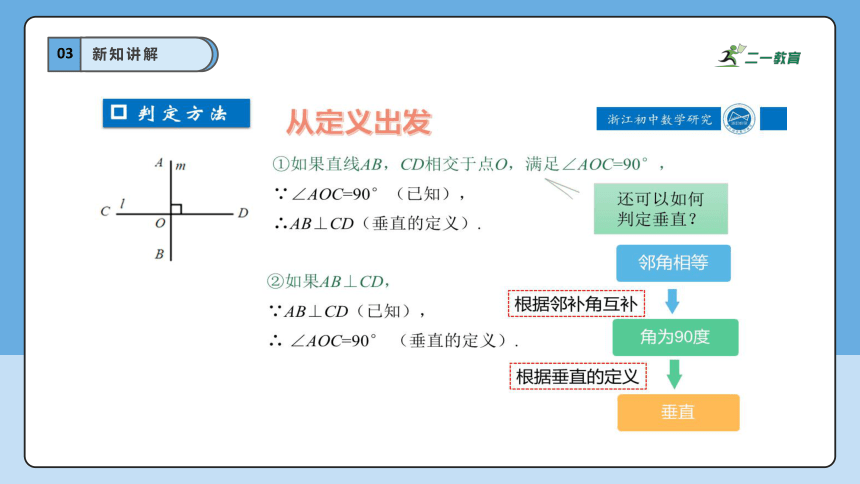
新知讲解
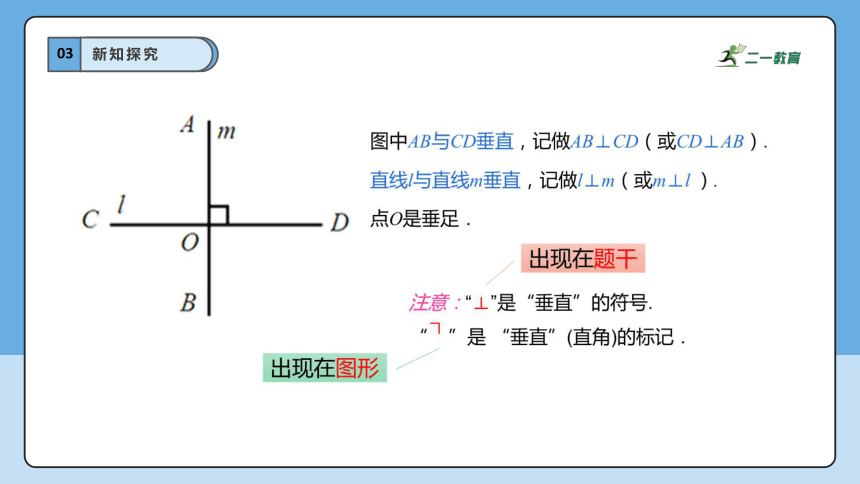
1.垂线的定义:当两条直线AB和CD所成的四个角中,如果有一个角是直角时,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.
2.垂直用符号 “⊥”来表示,读作“垂直于”.
如“直线AB垂直于直线CD”,就记作“AB⊥CD”.
O
A
B
C
D
3.交点O叫做垂足.
03
新知讲解
03
新知讲解
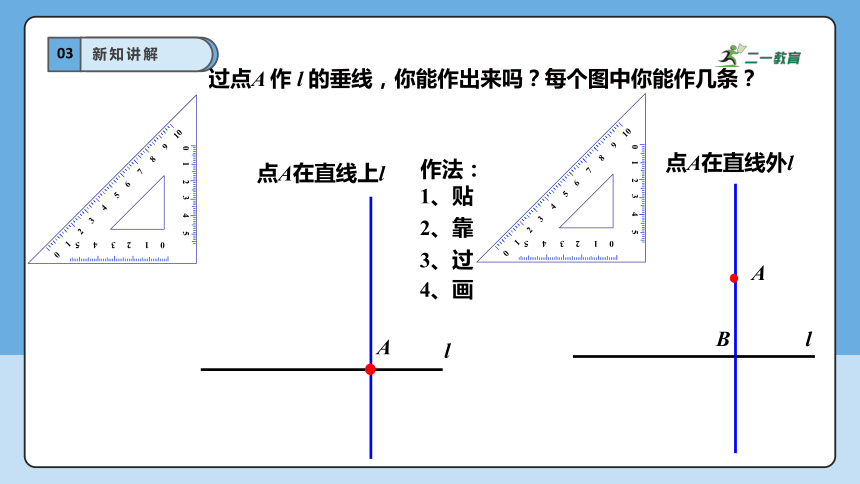
过点A 作 l 的垂线,你能作出来吗?每个图中你能作几条?
作法:
1、贴
2、靠
3、过
l
l
A
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
4、画
点A在直线上l
点A在直线外l
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
B
03
新知讲解
P
A B
你会用量角器过点P画直线AB的垂线吗?
过直线AB上一点P画AB的垂线,可以画几条?若点P在直线AB外呢?
垂线的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
新课探究
例3
如图,直线AB与直线CD相交于点O,OE⊥AB.已知∠BOD=45°,求∠ COE的度数.
解:∵OE⊥AB,
∴∠AOE=90°,
(垂直的定义)
∵∠AOC=∠BOD=45°,
∴∠COE=∠AOE+∠AOC=90°+45°=135°.
(对顶角相等)
03
新知讲解
如图,点P是直线l外的一点,画PO⊥l于O,线段PO称为点P到直线l的垂线段.点P与直线l上所有各点之间的距离中,哪一个距离最小?你能设计一个实验来验证你的判断吗?
答:点P与直线l上的点O距离最小.
测量法或叠合法验证.
根据圆的半径最短验证.
03
新知讲解
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.垂线段PO的长度,就是点P到直线l的距离.
已知P是直线外的一点,过点P画直线l的垂线,交直线l于点O,则线段PO叫做点P到直线l的垂线段.
直线外一点与直线上各点连结的所有线段中,垂线段最短.也可简单地说成:垂线段最短.
03
新知讲解
提炼概念
垂直定义:两条直线相交所构成的四个角中有一个是直角.
垂线的画法:三角尺和量角器 .
垂直的表示方法:用符号“⊥”表示.
垂直的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
垂线段最短:直线外一点与直线上各点连结的所有线段中,垂线段最短.
点到直线的距离:从直线外一点到这条直线的垂线段的长度.
04
课堂练习
【知识技能类作业】必做题:
1、点到直线的距离是指( )
A.从直线外一点到这条直线的垂线
B.从直线外一点到这条直线的垂线段
C.从直线外一点到这条直线的垂线的长
D.从直线外一点到这条直线的垂线段的长
D
04
课堂练习
【知识技能类作业】选做题:
2.已知,AD⊥BD,AE⊥BE,且AD=3,BE=4,CD=2,BC=5,则点B到
AC的距离为__ __,点A到BC的距离为__ __,点B到AD的距离为__ __.
4
3
7
04
课堂练习
【综合拓展类作业】
3.如图,直线AB与CD相交于点O,OE,OF分别是∠BOD,∠AOD的平分线.
(1)∠DOE的补角是__________________;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由.
解:(1)因为OE是∠BOD的平分线,
所以∠DOE=∠BOE,
又因为∠BOE+∠AOE=180°,∠DOE+∠COE=180°,
所以∠DOE的补角是∠AOE或∠COE.
∠AOE或∠COE
04
课堂练习
【综合拓展类作业】
04
课堂练习
【综合拓展类作业】
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
D
06
作业布置
【知识技能类作业】选做题:
2.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=________.
解:∵∠2和∠COE为对顶角 ∴∠2=∠COE=32° ∵∠1+∠COE+∠BOE=180° 即95°+32°+∠BOE=180° ∴∠BOE=53° 故答案为:53°。
06
作业布置
【综合拓展类作业】
解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
3.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.1.2直线的相交
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
2.掌握垂线的性质及垂线段的性质.
1.了解垂线、垂线段、点到直线的距离等概念;
02
新知导入
03
新知探究
α
a
b
b
b
b
b
)
在相交线的模型中,固定木条a,转动木条b,
当α=90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
03
新知探究
03
新知讲解
1.垂线的定义:当两条直线AB和CD所成的四个角中,如果有一个角是直角时,我们就说这两条直线互相垂直.其中一条直线叫做另一条直线的垂线.
2.垂直用符号 “⊥”来表示,读作“垂直于”.
如“直线AB垂直于直线CD”,就记作“AB⊥CD”.
O
A
B
C
D
3.交点O叫做垂足.
03
新知讲解
03
新知讲解
过点A 作 l 的垂线,你能作出来吗?每个图中你能作几条?
作法:
1、贴
2、靠
3、过
l
l
A
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
4、画
点A在直线上l
点A在直线外l
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
B
03
新知讲解
P
A B
你会用量角器过点P画直线AB的垂线吗?
过直线AB上一点P画AB的垂线,可以画几条?若点P在直线AB外呢?
垂线的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
新课探究
例3
如图,直线AB与直线CD相交于点O,OE⊥AB.已知∠BOD=45°,求∠ COE的度数.
解:∵OE⊥AB,
∴∠AOE=90°,
(垂直的定义)
∵∠AOC=∠BOD=45°,
∴∠COE=∠AOE+∠AOC=90°+45°=135°.
(对顶角相等)
03
新知讲解
如图,点P是直线l外的一点,画PO⊥l于O,线段PO称为点P到直线l的垂线段.点P与直线l上所有各点之间的距离中,哪一个距离最小?你能设计一个实验来验证你的判断吗?
答:点P与直线l上的点O距离最小.
测量法或叠合法验证.
根据圆的半径最短验证.
03
新知讲解
从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.垂线段PO的长度,就是点P到直线l的距离.
已知P是直线外的一点,过点P画直线l的垂线,交直线l于点O,则线段PO叫做点P到直线l的垂线段.
直线外一点与直线上各点连结的所有线段中,垂线段最短.也可简单地说成:垂线段最短.
03
新知讲解
提炼概念
垂直定义:两条直线相交所构成的四个角中有一个是直角.
垂线的画法:三角尺和量角器 .
垂直的表示方法:用符号“⊥”表示.
垂直的性质:在同一平面内,过一点有且仅有一条直线垂直于已知直线.
垂线段最短:直线外一点与直线上各点连结的所有线段中,垂线段最短.
点到直线的距离:从直线外一点到这条直线的垂线段的长度.
04
课堂练习
【知识技能类作业】必做题:
1、点到直线的距离是指( )
A.从直线外一点到这条直线的垂线
B.从直线外一点到这条直线的垂线段
C.从直线外一点到这条直线的垂线的长
D.从直线外一点到这条直线的垂线段的长
D
04
课堂练习
【知识技能类作业】选做题:
2.已知,AD⊥BD,AE⊥BE,且AD=3,BE=4,CD=2,BC=5,则点B到
AC的距离为__ __,点A到BC的距离为__ __,点B到AD的距离为__ __.
4
3
7
04
课堂练习
【综合拓展类作业】
3.如图,直线AB与CD相交于点O,OE,OF分别是∠BOD,∠AOD的平分线.
(1)∠DOE的补角是__________________;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由.
解:(1)因为OE是∠BOD的平分线,
所以∠DOE=∠BOE,
又因为∠BOE+∠AOE=180°,∠DOE+∠COE=180°,
所以∠DOE的补角是∠AOE或∠COE.
∠AOE或∠COE
04
课堂练习
【综合拓展类作业】
04
课堂练习
【综合拓展类作业】
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.如图,AB⊥AC,AD⊥BC,垂足分别为A,D,则图中能表示点到直线距离的线段共有( )
A.2条 B.3条 C.4条 D.5条
D
06
作业布置
【知识技能类作业】选做题:
2.如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=________.
解:∵∠2和∠COE为对顶角 ∴∠2=∠COE=32° ∵∠1+∠COE+∠BOE=180° 即95°+32°+∠BOE=180° ∴∠BOE=53° 故答案为:53°。
06
作业布置
【综合拓展类作业】
解:(1)∠COE的邻补角为∠COF和∠EOD;
(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF;
(3)∵∠BOF=90°,
∴AB⊥EF
∴∠AOF=90°,
又∵∠AOC=∠BOD=60°
∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
3.如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
