1.2同位角、内错角、同旁内角 课件(共28张PPT)
文档属性
| 名称 | 1.2同位角、内错角、同旁内角 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-01 08:27:41 | ||
图片预览



文档简介
(共28张PPT)
第一章 直角三角形
1.2同位角、内错角、同旁内角
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.理解同位角、内错角、同旁内角的概念,并能判断它们.
2.会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
02
新知导入
思考:
1.平面上两条直线有几种位置关系?
2.两条直线相交构成几个角 它们之间是什么置关系的角?
03
新知探究
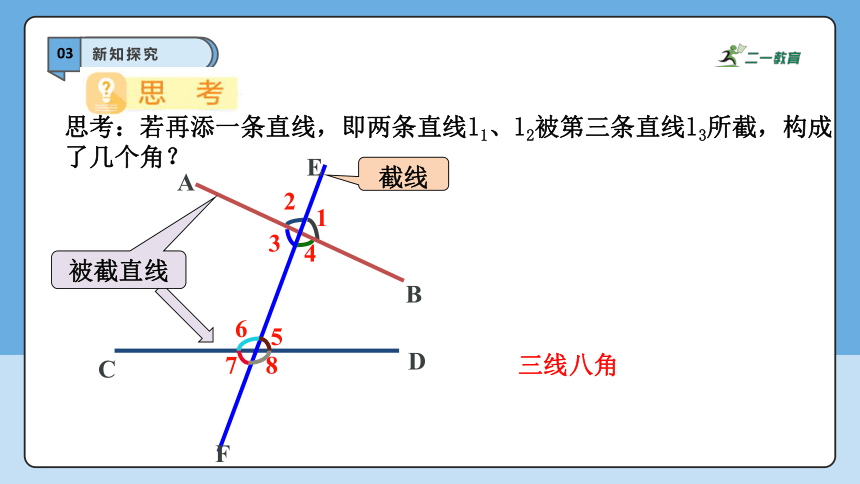
思考:若再添一条直线,即两条直线l1、l2被第三条直线l3所截,构成了几个角?
1
2
3
4
A
B
6
7
5
8
C
D
E
F
截线
被截直线
三线八角
03
新知探究
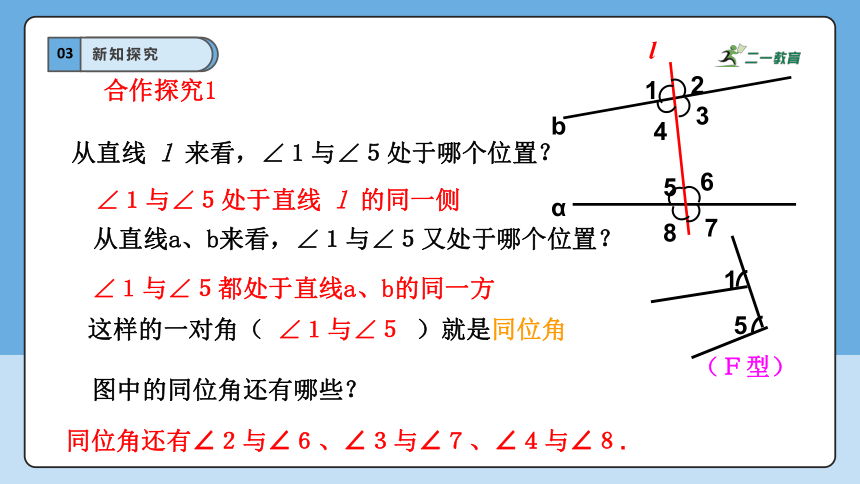
∠1与∠5处于直线 l 的同一侧
∠1与∠5都处于直线a、b的同一方
从直线a、b来看,∠1与∠5又处于哪个位置?
从直线 l 来看,∠1与∠5处于哪个位置?
这样的一对角( ∠1与∠5 )就是同位角
图中的同位角还有哪些?
同位角还有∠2与∠6、∠3与∠7、∠4与∠8.
l
α
b
1
2
3
4
5
8
7
6
(F型)
1
5
合作探究1
03
新知讲解
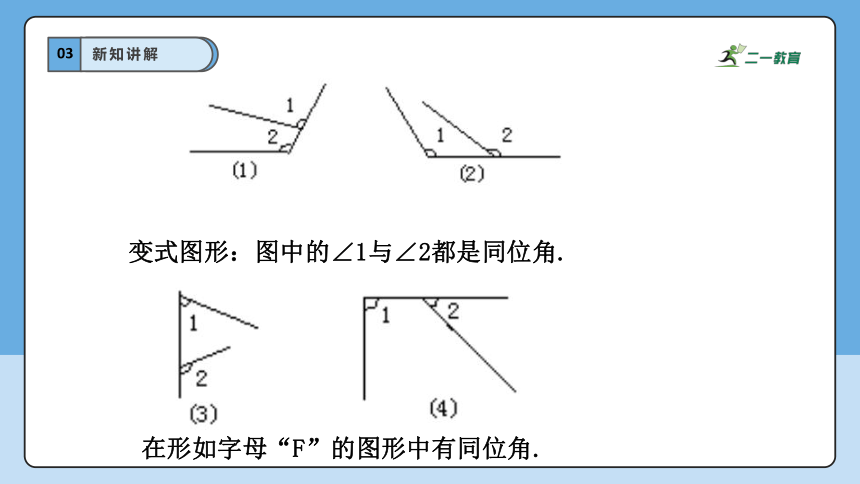
在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
03
新知讲解
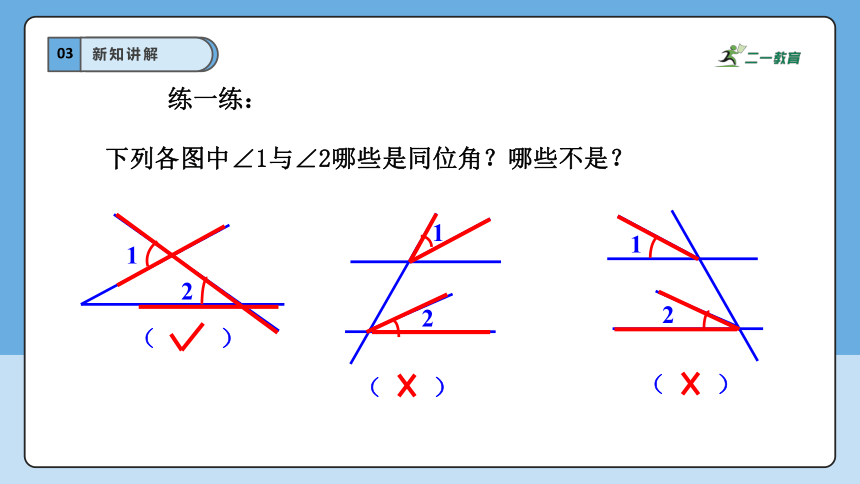
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
( )
1
2
( )
1
2
练一练:
03
新知讲解
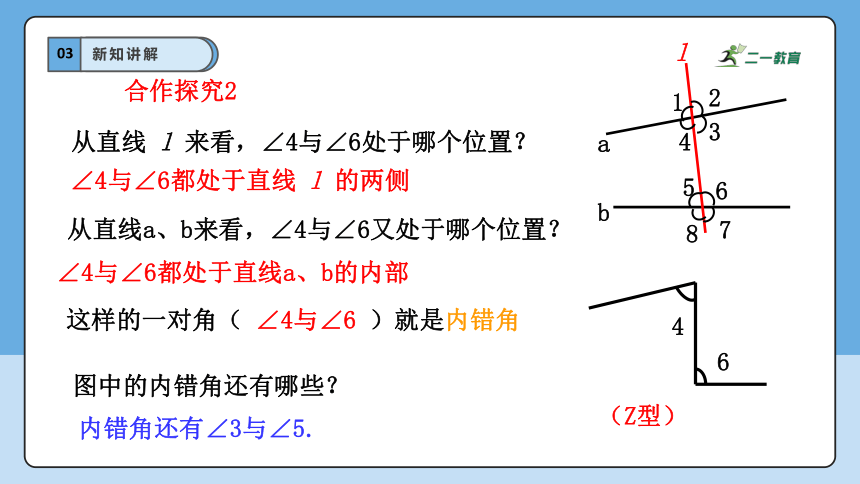
从直线 l 来看,∠4与∠6处于哪个位置?
∠4与∠6都处于直线 l 的两侧
从直线a、b来看,∠4与∠6又处于哪个位置?
∠4与∠6都处于直线a、b的内部
这样的一对角( ∠4与∠6 )就是内错角
图中的内错角还有哪些?
内错角还有∠3与∠5.
(Z型)
l
b
a
1
2
3
4
5
8
7
6
4
6
合作探究2
03
新知讲解
变式图形:图中的∠1与∠2都是内错角
图形特征:在形如“Z”的图形中有内错角.
03
新知讲解
(1)若ED,BC被AF所截,
则∠3与_____是内错角.
∠4
(2)∠1与∠3是AB与和AF被_____所截构成的_______角.
DE
内错
练一练:
完成下列填空:
03
新知讲解
从直线 l 来看,∠4与∠5处于哪个位置?
∠4与∠5处于直线 l 的同一侧
从直线a、b来看,∠4与∠5又处于哪个位置?
这样的一对角( ∠4与∠5 )就是同旁内角
图中的同旁内角还有哪些?
同旁内角还有∠3与∠6.
∠4与∠5都处于直线a、b的内部
(U 型)
l
α
b
1
2
3
4
5
8
7
6
4
5
合作探究3
03
新知讲解
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“n”的图形中有同旁内角。
03
新知讲解
同位角、内错角和同旁内角的结构特征:
截线 被截线 结构特征
同位角
内错角
同旁内角
“三线八角”
知识梳理
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
新课探究
例1
如图,直线DE截AB,AC,构成8个角。指出所有的同位角、内错角和同旁内角.
关键:要先分清哪两条直线被哪一条直线所截
同位角:∠2和∠5、∠1和∠8、
∠3和∠6、∠4和∠7
内错角:∠4和∠5、∠1和∠6
同旁内角:∠1和∠5、∠4和∠6
1
2
3
4
5
6
7
8
A
B
C
E
03
新知讲解
例2:如图,直线DE交∠ABC的边BA于点F.如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补. 请说明理由.
03
新知讲解
解:∵ ∠2与∠4是对顶角,
∴ ∠2=∠4.
已知∠1与∠2 ∴ ∠1=∠4.
∵∠2与∠3互为补角
∴ ∠2+∠3=180 . ∴ ∠1+∠3=180 .
即∠1与∠3互补.
03
新知讲解
提炼概念
【点悟】要把握好对顶角及三线八角的本质特征,两条直线相交有两对对顶角,三条直线两两相交,共会出现6对对顶角,同时出现6对内错角和6对同旁边内角和12对同位角.
04
课堂练习
【知识技能类作业】必做题:
1.下列图形中,∠1与∠2不是同位角的是 ( )
A B C D
D
04
课堂练习
【知识技能类作业】选做题:
2.如图所示,直线AB,CD,EF两两相交于点O,P,Q.
(1)试写出图中所有的对顶角;
(2)试写出∠QOP的同位角、内错角、同旁内角.
04
课堂练习
【知识技能类作业】选做题:
解:(1)∠EQD与∠CQF,∠EQC与∠DQF,AOD与∠BOC,∠AOC与∠DOB,∠EPB与∠APF,APE与∠BPF分别是对顶角,图中共有6对.
(2)∠QOP的同位角有:∠DQF,∠EPB.∠QOP的内错角有:∠EQC,∠APF.∠QOP的同旁内角有:∠OQF,∠QPO.
04
课堂练习
【综合拓展类作业】
3.如图,Rt△ABC中,∠C=90°,DE⊥AC,交AB于点D,交AC于点E.(1)说出当BC,DE被AB所截时,∠3的同位角、内错角和同旁内角;
(2)试说明∠1=∠2=∠3的理由.
解:(1)∠3的同位角是∠1,∠3的内错角是∠2,∠3的同旁内角是∠BDE.
(2)∵∠C=90°,∴∠3+∠A=90°.
∵DE⊥AC,∴∠1+∠A=90°,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3,∴∠1=∠2=∠3.
05
课堂小结
主要内容:
1、三种角产生的条件及位置特征;
2、判断时应先找到“截线”,再找另外两
直线,然后根据角的位置决定是哪一种角.
3、当图形复杂时可把暂时不需要的线段、
角等遮住,也可采用图形分解法、图形
涂色法以排除干扰.
两条直线被第三条直线所截而
产生的三种角——同位角、内错角、同旁内角.
06
作业布置
【知识技能类作业】必做题:
1.如图所示,按几组角的位置,下列判断错误
的是 ( )
A.∠1和∠2是同旁内角
B.∠3和∠4是内错角
C.∠5和∠6是同旁内角
D.∠5和∠8是同位角
C
06
作业布置
【知识技能类作业】选做题:
2.如图,下列说法正确的是:
①能与∠EDF构成内错角的有2个
②能与∠BFD构成同位角的有2个
③能与∠C构成同旁内角的角有4个
其中结论正确的是( )
A.①② B.②③ C.① D.①③
C
解析:②能与∠BFD构成同位角的角有∠DCF
③能与∠C构成同旁内角的角有:∠CDF、∠CDE、∠CFD、∠CBA、∠CBA、∠CAB共5个
06
作业布置
【综合拓展类作业】
3.探究题:
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有4对,内错角有 对,同旁内角有 对;
图1 图2
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有 对,内错角有 对,同旁内角有__对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有 对,内错角有 对,同旁内角有__________对.(用含n的式子表示)
2
2
6
12
6
2n(n-1)
n(n-1)
n(n-1)
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.2同位角、内错角、同旁内角
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.理解同位角、内错角、同旁内角的概念,并能判断它们.
2.会在给定某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
02
新知导入
思考:
1.平面上两条直线有几种位置关系?
2.两条直线相交构成几个角 它们之间是什么置关系的角?
03
新知探究
思考:若再添一条直线,即两条直线l1、l2被第三条直线l3所截,构成了几个角?
1
2
3
4
A
B
6
7
5
8
C
D
E
F
截线
被截直线
三线八角
03
新知探究
∠1与∠5处于直线 l 的同一侧
∠1与∠5都处于直线a、b的同一方
从直线a、b来看,∠1与∠5又处于哪个位置?
从直线 l 来看,∠1与∠5处于哪个位置?
这样的一对角( ∠1与∠5 )就是同位角
图中的同位角还有哪些?
同位角还有∠2与∠6、∠3与∠7、∠4与∠8.
l
α
b
1
2
3
4
5
8
7
6
(F型)
1
5
合作探究1
03
新知讲解
在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
03
新知讲解
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
( )
1
2
( )
1
2
练一练:
03
新知讲解
从直线 l 来看,∠4与∠6处于哪个位置?
∠4与∠6都处于直线 l 的两侧
从直线a、b来看,∠4与∠6又处于哪个位置?
∠4与∠6都处于直线a、b的内部
这样的一对角( ∠4与∠6 )就是内错角
图中的内错角还有哪些?
内错角还有∠3与∠5.
(Z型)
l
b
a
1
2
3
4
5
8
7
6
4
6
合作探究2
03
新知讲解
变式图形:图中的∠1与∠2都是内错角
图形特征:在形如“Z”的图形中有内错角.
03
新知讲解
(1)若ED,BC被AF所截,
则∠3与_____是内错角.
∠4
(2)∠1与∠3是AB与和AF被_____所截构成的_______角.
DE
内错
练一练:
完成下列填空:
03
新知讲解
从直线 l 来看,∠4与∠5处于哪个位置?
∠4与∠5处于直线 l 的同一侧
从直线a、b来看,∠4与∠5又处于哪个位置?
这样的一对角( ∠4与∠5 )就是同旁内角
图中的同旁内角还有哪些?
同旁内角还有∠3与∠6.
∠4与∠5都处于直线a、b的内部
(U 型)
l
α
b
1
2
3
4
5
8
7
6
4
5
合作探究3
03
新知讲解
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“n”的图形中有同旁内角。
03
新知讲解
同位角、内错角和同旁内角的结构特征:
截线 被截线 结构特征
同位角
内错角
同旁内角
“三线八角”
知识梳理
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
新课探究
例1
如图,直线DE截AB,AC,构成8个角。指出所有的同位角、内错角和同旁内角.
关键:要先分清哪两条直线被哪一条直线所截
同位角:∠2和∠5、∠1和∠8、
∠3和∠6、∠4和∠7
内错角:∠4和∠5、∠1和∠6
同旁内角:∠1和∠5、∠4和∠6
1
2
3
4
5
6
7
8
A
B
C
E
03
新知讲解
例2:如图,直线DE交∠ABC的边BA于点F.如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补. 请说明理由.
03
新知讲解
解:∵ ∠2与∠4是对顶角,
∴ ∠2=∠4.
已知∠1与∠2 ∴ ∠1=∠4.
∵∠2与∠3互为补角
∴ ∠2+∠3=180 . ∴ ∠1+∠3=180 .
即∠1与∠3互补.
03
新知讲解
提炼概念
【点悟】要把握好对顶角及三线八角的本质特征,两条直线相交有两对对顶角,三条直线两两相交,共会出现6对对顶角,同时出现6对内错角和6对同旁边内角和12对同位角.
04
课堂练习
【知识技能类作业】必做题:
1.下列图形中,∠1与∠2不是同位角的是 ( )
A B C D
D
04
课堂练习
【知识技能类作业】选做题:
2.如图所示,直线AB,CD,EF两两相交于点O,P,Q.
(1)试写出图中所有的对顶角;
(2)试写出∠QOP的同位角、内错角、同旁内角.
04
课堂练习
【知识技能类作业】选做题:
解:(1)∠EQD与∠CQF,∠EQC与∠DQF,AOD与∠BOC,∠AOC与∠DOB,∠EPB与∠APF,APE与∠BPF分别是对顶角,图中共有6对.
(2)∠QOP的同位角有:∠DQF,∠EPB.∠QOP的内错角有:∠EQC,∠APF.∠QOP的同旁内角有:∠OQF,∠QPO.
04
课堂练习
【综合拓展类作业】
3.如图,Rt△ABC中,∠C=90°,DE⊥AC,交AB于点D,交AC于点E.(1)说出当BC,DE被AB所截时,∠3的同位角、内错角和同旁内角;
(2)试说明∠1=∠2=∠3的理由.
解:(1)∠3的同位角是∠1,∠3的内错角是∠2,∠3的同旁内角是∠BDE.
(2)∵∠C=90°,∴∠3+∠A=90°.
∵DE⊥AC,∴∠1+∠A=90°,∴∠1=∠3.
又∵∠1=∠2,∴∠2=∠3,∴∠1=∠2=∠3.
05
课堂小结
主要内容:
1、三种角产生的条件及位置特征;
2、判断时应先找到“截线”,再找另外两
直线,然后根据角的位置决定是哪一种角.
3、当图形复杂时可把暂时不需要的线段、
角等遮住,也可采用图形分解法、图形
涂色法以排除干扰.
两条直线被第三条直线所截而
产生的三种角——同位角、内错角、同旁内角.
06
作业布置
【知识技能类作业】必做题:
1.如图所示,按几组角的位置,下列判断错误
的是 ( )
A.∠1和∠2是同旁内角
B.∠3和∠4是内错角
C.∠5和∠6是同旁内角
D.∠5和∠8是同位角
C
06
作业布置
【知识技能类作业】选做题:
2.如图,下列说法正确的是:
①能与∠EDF构成内错角的有2个
②能与∠BFD构成同位角的有2个
③能与∠C构成同旁内角的角有4个
其中结论正确的是( )
A.①② B.②③ C.① D.①③
C
解析:②能与∠BFD构成同位角的角有∠DCF
③能与∠C构成同旁内角的角有:∠CDF、∠CDE、∠CFD、∠CBA、∠CBA、∠CAB共5个
06
作业布置
【综合拓展类作业】
3.探究题:
(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有4对,内错角有 对,同旁内角有 对;
图1 图2
(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有 对,内错角有 对,同旁内角有__对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有 对,内错角有 对,同旁内角有__________对.(用含n的式子表示)
2
2
6
12
6
2n(n-1)
n(n-1)
n(n-1)
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
