1.4.2 平行线的判定 课件(共19张PPT)
文档属性
| 名称 | 1.4.2 平行线的判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-03 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
第一章 直角三角形
1.4.2平行线的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.掌握平行线的判定方法二、三,并能运用其进行简单的推理.
2.能把实际问题转化为平行线判定的基本图形.
02
新知导入
定义:在同一平面内,不相交的两条直线叫平行线.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
判定两条直线平行的方法有两种:
同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?
符号语言:如图
∵ ∠1=∠2(已知)
∴ l1∥l2
(同位角相等,两直线平行)
2
1
l2
A
l1
03
新知探究
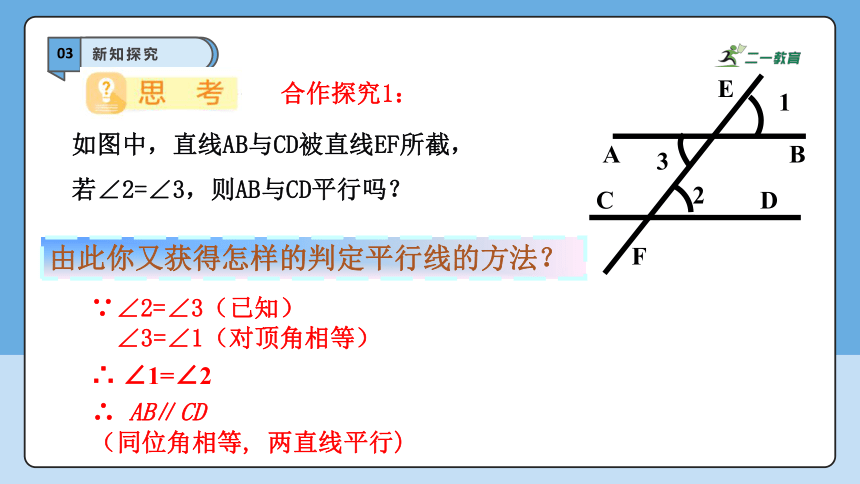
如图中,直线AB与CD被直线EF所截,
若∠2=∠3,则AB与CD平行吗?
∵∠2=∠3(已知)
∠3=∠1(对顶角相等)
∴ ∠1=∠2
∴ AB∥CD
(同位角相等, 两直线平行)
由此你又获得怎样的判定平行线的方法?
B
3
A
C
D
F
1
2
E
合作探究1:
03
新知探究
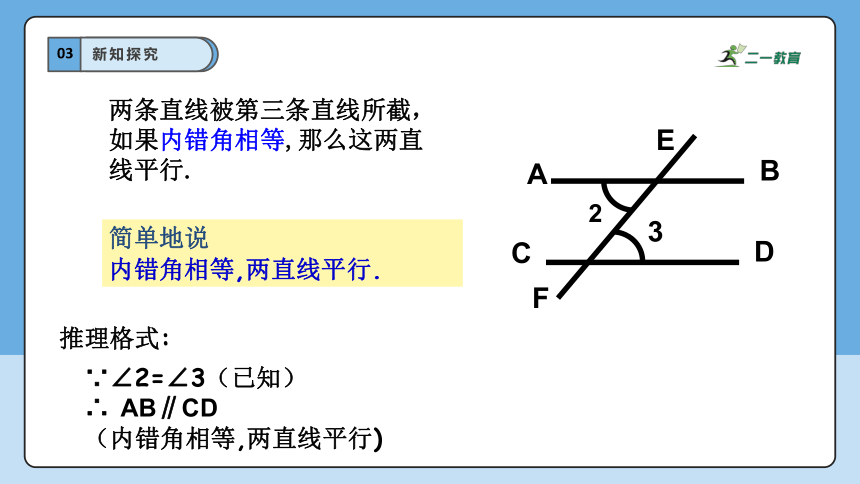
∵∠2=∠3(已知)
∴ AB∥CD
(内错角相等,两直线平行)
推理格式:
两条直线被第三条直线所截,如果内错角相等,那么这两直线平行.
B
2
3
A
D
E
F
C
简单地说
内错角相等,两直线平行.
03
新知讲解
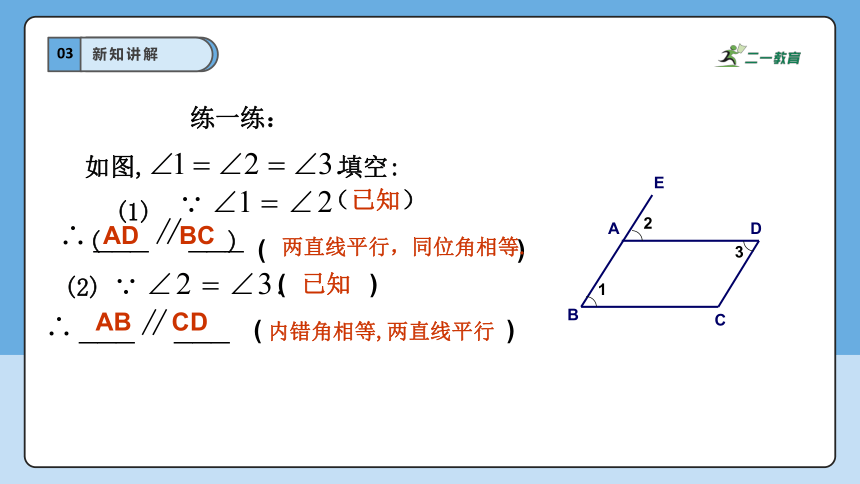
如图, 填空:
(1) ( )
(2)
( )
( )
( )
D
C
B
A
E
3
2
1
(已知)
已知
AB
BC
CD
AD
内错角相等,两直线平行
两直线平行,同位角相等.
练一练:
03
新知讲解
如图中,直线AB与CD被直线EF所截 ,若∠2+∠4=180°,则AB与CD平行吗?
由此你又获得怎样的判定平行线的方法?
E
A
B
C
D
F
1
4
2
3
理由:
∵ ∠1+∠4=180°
又∵ ∠2+∠4=180°(已知) ∴ ∠1=∠2
∴ AB∥CD(同位角相等,两直线平行)
合作探究2:
03
新知讲解
两条直线被第三条直线所截,如果同旁内角互补,那么这两直线平行.
简单地说
同旁内角互补,两直线平行.
推理格式:
2
B
A
C
D
E
F
3
∵ ∠2+∠3=180 °(已知)
∴ AB∥CD
(同旁内角互补, 两直线平行)
新课探究
例4
E
AP平分∠BAC,CP平分∠ACD,
∠1+∠2=90°,判断AB,CD是否平行,说明理由.
解: AC//CD.理由如下: AP平分∠BAC,CP平分∠ACD,根据角平分线的意义,知∠1=1/2∠BAC ,∠2=1/2∠ACD
∴∠BAC+ ∠ACD= 2(∠1+∠2)
=2×90°=180°
∴ AC//CD (同旁内角互补,两直线平行)
04
课堂练习
【知识技能类作业】必做题:
1.如图,下列判断错误的是 ( )
A.如果∠1=∠2,那么l3∥l4
B.如果∠3=∠5,那么l3∥l4
C.如果∠1=∠3,那么l3∥l4
D.如果∠2=∠3,那么l1∥l2
C
04
课堂练习
【知识技能类作业】选做题:
2.如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么?
解:DE∥AF,理由如下:
∵CD⊥DA,DA⊥AB,∴∠CDA=∠DAB=90°,
∴CD∥AB,
∵∠1=∠2,∴∠CDA-∠1=∠DAB-∠2,
∴∠3=∠4,∴DE∥AF.
04
课堂练习
【综合拓展类作业】
3.如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.
解:∵DE平分∠ADC,∴∠ADC=2∠EDC.
∵∠CE平分∠BCD,∴∠BCD=2∠DCE,
∴∠ADC+∠BCD=2∠EDC+2∠DCE.
又∵∠EDC+∠DCE=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC(同旁内角互补,两直线平行).
05
课堂小结
1.平行线的判定方法(二)
内容:两条直线被第三条直线所截,如果_________相等,那么这两条直线平行.简单地说, ______________ ,两直线平行.
2.平行线的判定方法(三)
内容:两条直线被第三条直线所截,如果___________互补,那么这两条直线平等.简单地说, _____________,两直线平行.
内错角
内错角相等
同旁内角
同旁内角互补
06
作业布置
【知识技能类作业】必做题:
1.如图,下列给出的条件中,不能判定AB∥DF的是
( )
A.∠A+∠2=180° B.∠A=∠3
C.∠1=∠4 D.∠1=∠A
A选项正确,同旁内角互补,两直线平行;B选项正确,同位角相等,两直线平行;C选项正确,内错角相等,两直线平行;D选项不能判定AB∥DF.
D
06
作业布置
【知识技能类作业】选做题:
2、如图,下列推理正确的有( )
①因为∠2=∠4,所以 AD∥BC;
②因为∠BAD+∠D=180°,所以 AD∥BC;
③因为∠1=∠3,所以 AD∥BC;
④因为∠1+∠2+∠B=180°,所以 AD∥BC.
A.1个 B.2个 C.3个 D.4个
B
分析:①中∠2 和∠4 的公共边所在的直线(截线)是AC,另外两边所在的直线(被截线)分别是 AB 和 CD,所以由∠2=∠4 得 AB∥CD,所以①错误;同理由∠BAD+∠D=180°,可得 AD∥BC,所以②错误.
06
作业布置
【综合拓展类作业】
3、如图,在⊿ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F。
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,试判断DG与BC的位置关系,并说明理由。
解:(1)CD与EF平行.理由如下:
∵CD⊥AB,EF⊥AB,
∵垂直于同一直线的两直线互相平行,
∴CD∥EF;
(2)DG∥BC理由如下:
∵CD∥EF;∴∠2=∠DCE
∵∠1=∠2;∴∠1=∠DCE ∴DG∥BC
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
1.4.2平行线的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.掌握平行线的判定方法二、三,并能运用其进行简单的推理.
2.能把实际问题转化为平行线判定的基本图形.
02
新知导入
定义:在同一平面内,不相交的两条直线叫平行线.
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
判定两条直线平行的方法有两种:
同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?
符号语言:如图
∵ ∠1=∠2(已知)
∴ l1∥l2
(同位角相等,两直线平行)
2
1
l2
A
l1
03
新知探究
如图中,直线AB与CD被直线EF所截,
若∠2=∠3,则AB与CD平行吗?
∵∠2=∠3(已知)
∠3=∠1(对顶角相等)
∴ ∠1=∠2
∴ AB∥CD
(同位角相等, 两直线平行)
由此你又获得怎样的判定平行线的方法?
B
3
A
C
D
F
1
2
E
合作探究1:
03
新知探究
∵∠2=∠3(已知)
∴ AB∥CD
(内错角相等,两直线平行)
推理格式:
两条直线被第三条直线所截,如果内错角相等,那么这两直线平行.
B
2
3
A
D
E
F
C
简单地说
内错角相等,两直线平行.
03
新知讲解
如图, 填空:
(1) ( )
(2)
( )
( )
( )
D
C
B
A
E
3
2
1
(已知)
已知
AB
BC
CD
AD
内错角相等,两直线平行
两直线平行,同位角相等.
练一练:
03
新知讲解
如图中,直线AB与CD被直线EF所截 ,若∠2+∠4=180°,则AB与CD平行吗?
由此你又获得怎样的判定平行线的方法?
E
A
B
C
D
F
1
4
2
3
理由:
∵ ∠1+∠4=180°
又∵ ∠2+∠4=180°(已知) ∴ ∠1=∠2
∴ AB∥CD(同位角相等,两直线平行)
合作探究2:
03
新知讲解
两条直线被第三条直线所截,如果同旁内角互补,那么这两直线平行.
简单地说
同旁内角互补,两直线平行.
推理格式:
2
B
A
C
D
E
F
3
∵ ∠2+∠3=180 °(已知)
∴ AB∥CD
(同旁内角互补, 两直线平行)
新课探究
例4
E
AP平分∠BAC,CP平分∠ACD,
∠1+∠2=90°,判断AB,CD是否平行,说明理由.
解: AC//CD.理由如下: AP平分∠BAC,CP平分∠ACD,根据角平分线的意义,知∠1=1/2∠BAC ,∠2=1/2∠ACD
∴∠BAC+ ∠ACD= 2(∠1+∠2)
=2×90°=180°
∴ AC//CD (同旁内角互补,两直线平行)
04
课堂练习
【知识技能类作业】必做题:
1.如图,下列判断错误的是 ( )
A.如果∠1=∠2,那么l3∥l4
B.如果∠3=∠5,那么l3∥l4
C.如果∠1=∠3,那么l3∥l4
D.如果∠2=∠3,那么l1∥l2
C
04
课堂练习
【知识技能类作业】选做题:
2.如图,已知CD⊥DA,DA⊥AB,∠1=∠2,问直线DE与AF是否平行?为什么?
解:DE∥AF,理由如下:
∵CD⊥DA,DA⊥AB,∴∠CDA=∠DAB=90°,
∴CD∥AB,
∵∠1=∠2,∴∠CDA-∠1=∠DAB-∠2,
∴∠3=∠4,∴DE∥AF.
04
课堂练习
【综合拓展类作业】
3.如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.
解:∵DE平分∠ADC,∴∠ADC=2∠EDC.
∵∠CE平分∠BCD,∴∠BCD=2∠DCE,
∴∠ADC+∠BCD=2∠EDC+2∠DCE.
又∵∠EDC+∠DCE=90°,
∴∠ADC+∠BCD=180°,
∴AD∥BC(同旁内角互补,两直线平行).
05
课堂小结
1.平行线的判定方法(二)
内容:两条直线被第三条直线所截,如果_________相等,那么这两条直线平行.简单地说, ______________ ,两直线平行.
2.平行线的判定方法(三)
内容:两条直线被第三条直线所截,如果___________互补,那么这两条直线平等.简单地说, _____________,两直线平行.
内错角
内错角相等
同旁内角
同旁内角互补
06
作业布置
【知识技能类作业】必做题:
1.如图,下列给出的条件中,不能判定AB∥DF的是
( )
A.∠A+∠2=180° B.∠A=∠3
C.∠1=∠4 D.∠1=∠A
A选项正确,同旁内角互补,两直线平行;B选项正确,同位角相等,两直线平行;C选项正确,内错角相等,两直线平行;D选项不能判定AB∥DF.
D
06
作业布置
【知识技能类作业】选做题:
2、如图,下列推理正确的有( )
①因为∠2=∠4,所以 AD∥BC;
②因为∠BAD+∠D=180°,所以 AD∥BC;
③因为∠1=∠3,所以 AD∥BC;
④因为∠1+∠2+∠B=180°,所以 AD∥BC.
A.1个 B.2个 C.3个 D.4个
B
分析:①中∠2 和∠4 的公共边所在的直线(截线)是AC,另外两边所在的直线(被截线)分别是 AB 和 CD,所以由∠2=∠4 得 AB∥CD,所以①错误;同理由∠BAD+∠D=180°,可得 AD∥BC,所以②错误.
06
作业布置
【综合拓展类作业】
3、如图,在⊿ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F。
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,试判断DG与BC的位置关系,并说明理由。
解:(1)CD与EF平行.理由如下:
∵CD⊥AB,EF⊥AB,
∵垂直于同一直线的两直线互相平行,
∴CD∥EF;
(2)DG∥BC理由如下:
∵CD∥EF;∴∠2=∠DCE
∵∠1=∠2;∴∠1=∠DCE ∴DG∥BC
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
