1.4.2平行线的判定 教案

中小学教育资源及组卷应用平台
分课时教学设计
第6课时《1.4.2平行线的判定 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 通过同位角、内错角、同旁内角的关系证明直线平行，掌握平行线的判定方法二、三．
学习者分析 要判定两直线是否平行，首先要将题目给出的角转化为这两条直线被第三条直线所截构成的同位角、内错角或同旁内角，再看它们这些角是否满足平行的判定条件.
教学目标 掌握平行线的判定方法二、三，并能运用其进行简单的推理．
教学重点 平行线的判定方法二、三的发现、推理和应用．
教学难点 平行线的判定方法二、三的推理和应用．
学习活动设计
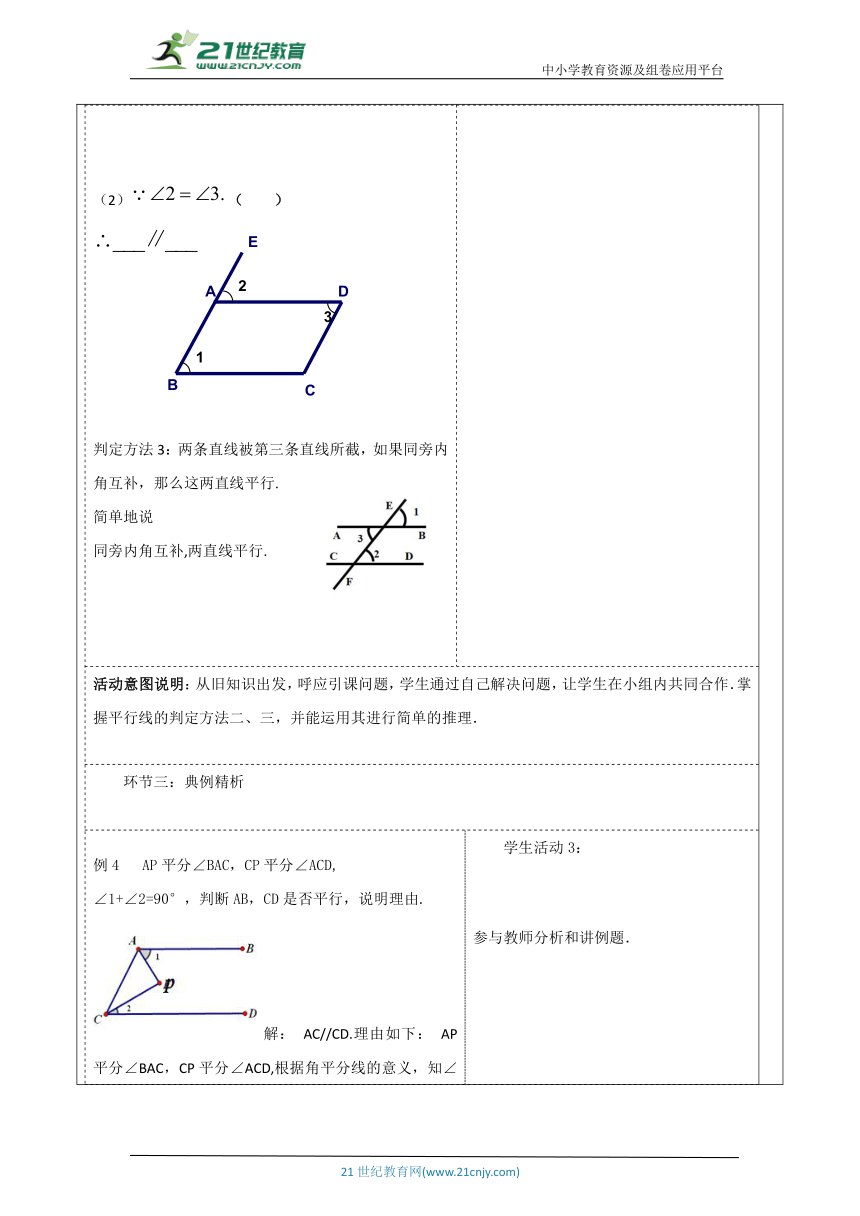
教师活动学生活动环节一：引入新课 判定两条直线平行的方法有两种： 1.定义：在同一平面内，不相交的两条直线叫平行线. 2.两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行. 符号语言：如图∵ ∠1=∠3（已知） ∴ l1∥l2 （同位角相等，两直线平行） 同学们可以想一想？ 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，进行探索.通过同位角、内错角、同旁内角的关系证明直线平行． 环节二：新知探究除应用以上两种方法以外，是否还有其它方法呢？ 合作探究1： 如图中，直线AB与CD被直线EF所截， 若∠2=∠3，则AB与CD平行吗？ 由此你又获得怎样的判定平行线的方法？ ∵∠2=∠3（已知） ∠3=∠1（对顶角相等） ∴ ∠1=∠2 ∴ AB∥CD （同位角相等, 两直线平行) 合作探究2： 如图中,直线AB与CD被直线EF所截 ，若∠2+∠4=180°，则AB与CD平行吗？ 由此你又获得怎样的判定平行线的方法？ 理由: ∵ ∠1+∠4=180° 又∵ ∠2+∠4=180°(已知) ∴ ∠1=∠2 ∴ AB∥CD(同位角相等,两直线平行) 判定方法2： 两条直线被第三条直线所截，如果内错角相等,那么这两直线平行. 简单地说 内错角相等,两直线平行. 推理格式: ∵∠2=∠3（已知） ∴ AB∥CD （内错角相等,两直线平行) 练一练： 如图, 填空: （ ） 判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两直线平行. 简单地说 同旁内角互补,两直线平行. 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．掌握平行线的判定方法二、三，并能运用其进行简单的推理． 环节三：典例精析 例4 AP平分∠BAC，CP平分∠ACD, ∠1+∠2=90°，判断AB，CD是否平行，说明理由. 解： AC//CD.理由如下： AP平分∠BAC，CP平分∠ACD,根据角平分线的意义，知∠1=1/2∠BAC ,∠2=1/2∠ACD ∴∠BAC+ ∠ACD= 2（∠1+∠2） =2×90°=180° ∴ AC//CD （同旁内角互补，两直线平行） 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，掌握平行线的判定方法二、三的发现、推理和应用．
板书设计
课堂练习 【知识技能类作业】 必做题： 1．如图，下列判断错误的是 (　 　) A．如果∠1＝∠2，那么l3∥l4 B．如果∠3＝∠5，那么l3∥l4 C．如果∠1＝∠3，那么l3∥l4 D．如果∠2＝∠3，那么l1∥l2 选做题： 2如图，已知CD⊥DA，DA⊥AB，∠1=∠2，问直线DE与AF是否平行？为什么？ 【综合拓展类作业】 3．如图所示，已知点E在AB上，且CE平分∠BCD，DE平分∠ADC，∠EDC＋∠DCE＝90°，试说明AD∥BC.
课堂总结 归纳：判定两条直线平行的方法有： 1.同位角相等, 两直线平行. 2.内错角相等, 两直线平行. 3.同旁内角互补, 两直线平行. 4. 在同一平面内，垂直于同一条直线的两直线平行. 5.平行线的定义.
作业设计 【知识技能类作业】 必做题： 1．如图，下列给出的条件中，不能判定AB∥DF的是 (　 　) A．∠A＋∠2＝180° B．∠A＝∠3 C．∠1＝∠4 D．∠1＝∠A 选做题： 2、如图，下列推理正确的有（ ） ①因为∠2=∠4，所以 AD∥BC； ②因为∠BAD+∠D=180°，所以 AD∥BC； ③因为∠1=∠3，所以 AD∥BC； ④因为∠1+∠2+∠B=180°，所以 AD∥BC. A.1个 B.2个 C.3个 D.4个 【综合拓展类作业】 3、如图，在⊿ABC中，CD⊥AB,垂足为D，点E在BC上，EF⊥AB,垂足为F。 （1）CD与EF平行吗？为什么？ （2）如果∠1=∠2，试判断DG与BC的位置关系，并说明理由。
教学反思
21世纪教育网(www.21cnjy.com)