2.2 二元一次方程组和它的解 课件(共26张PPT)
文档属性
| 名称 | 2.2 二元一次方程组和它的解 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-06 20:52:48 | ||
图片预览






文档简介
(共26张PPT)
第二章 二元一次方程组
2.2二元一次方程组和它的解
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.理解并掌握二元一次方程组及其解的概念.
2.会用列表尝试的方法求二元一次方程组的解.
02
新知导入
1、判断下列各方程是不是二元一次方程?
√
×
×
2、下列各对数值中,是二元一次方程x-2y=7的解的是( )
B
A. B. C. D.
03
新知探究
每张成人票5元,每张儿童票3元.
昨天,我们8个人去红山公园玩,买门票花了34元.
到底去了几个成人,几个儿童呢?
03
新知探究
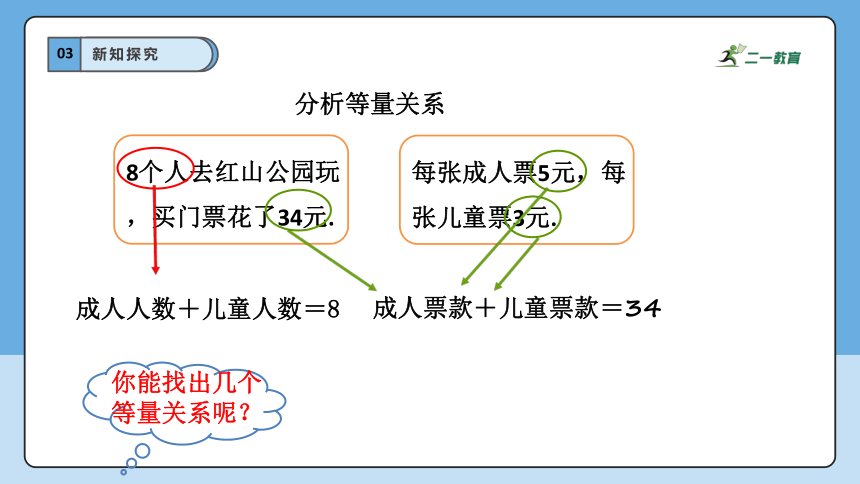
8个人去红山公园玩
,买门票花了34元.
每张成人票5元,每
张儿童票3元.
成人人数+儿童人数=8
成人票款+儿童票款=34
你能找出几个等量关系呢?
分析等量关系
03
新知讲解
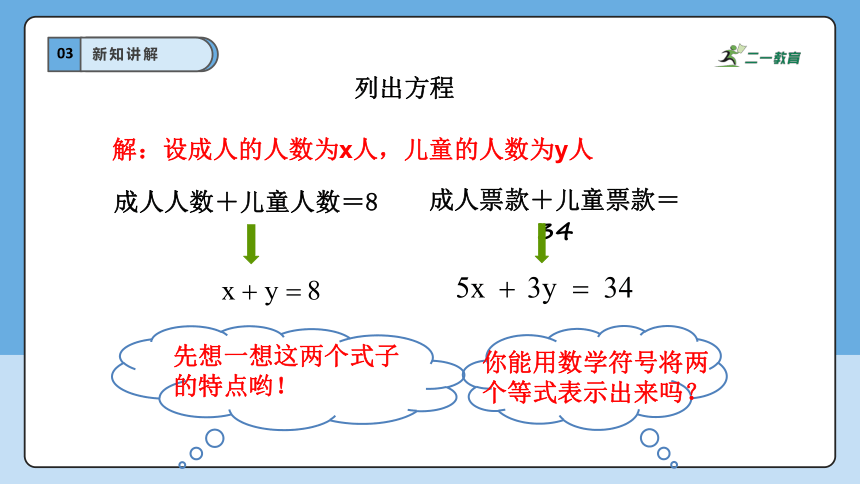
成人人数+儿童人数=8
成人票款+儿童票款=34
列出方程
你能用数学符号将两个等式表示出来吗?
解:设成人的人数为x人,儿童的人数为y人
先想一想这两个式子的特点哟!
03
新知讲解
解:
x,y都分别表示同一个未知数,x,y的值必须同时满足以上两个方程.即
x+y=200,
y=x+10.
x+y=200,
y=x+10.
一个苹果和一个梨的质量合计200g(如图1),这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等(如图2).问苹果和梨的质量各为多少g?
如果设苹果和梨的质量分别为x(g)和y(g),你能列出几个方程?
观察 ,想一想它有什么特点?
x+y=200
y=x+10
共同点:
2.两个方程共含有两个未知数.
1.由两个一次方程组成;
3.等号两边都是整式.
03
新知讲解
1. 定义:由两个一次方程组成,并且含有两个未知数的方程组,叫做二元一次方程组.
2. 要点精析:
二元一次方程组的条件:
(1)共含有两个未知数.
(2)每个方程都是一次方程.
注:二元一次方程组并不要求每个方程都是二元的,如 2-x=2
2x+y=5 也是二元一次方程组.
03
新知讲解
一元一次方程与二元一次方程的相同点与不同点:
方程 不同点 相同点 一元一次方程 未知个数数1个 含有未知数项的次数1次
整式方程
二元一次方程 未知个数数2个 含有未知数项的次数1次 03
新知讲解
(1)已知方程 x+y=200,填写下表:
(2)已知方程 y=x+10,填写下表:
问题:有没有这样的解,它既是方程x+y=200的一个解,又是方程y=x+10的一个解
x … 85 90 95 100 105 …
y … …
115
110
100
95
95
105
x … 85 90 95 100 105 …
y … 105 …
95
100
110
115
95
105
03
新知讲解
同时满足二元一次方程组中各个方程的解叫作二元一次方程组的解.
二元一次方程组的解:
x=95
y=105
例如: 是 的解.
x+y=200
y=x+10
注意: 二元一次方程组的解也要用大括号表示
提炼概念
新课探究
例1
E
03
新知讲解
04
课堂练习
【知识技能类作业】必做题:
1.下列是二元一次方程组的是 ( )
A
04
课堂练习
【知识技能类作业】选做题:
04
课堂练习
【综合拓展类作业】
3.已知两个自然数的和是67,差是3设这两个自然数分别是x,y。请列出关于x,y的方程组,并用列表尝试的方法求出这两个自然数。
解:根据题意可列出方程组:{
x+y=67
x-y=3
分析:列表的时候要注意数据的选择。
x … 32 33 34 35 36 37 38 …
y … 29 30 31 32 34 35 36 …
x=y … …
61
63
65
67
70
72
74
05
课堂小结
1.二元一次方程组
定义:由两个_______次方程组成,并且含有______个未知数的方程组,叫做二元一次方程组.
2.二元一次方程组的解
定义:_________满足二元一次方程组中各个方程的解,叫做这个二元一次方程组的解.
一
两
同时
06
作业布置
【知识技能类作业】必做题:
A.同时适合方程①和方程②的x,y的值是方程组的解
B.适合方程①的x,y的值是方程组的解
C.适合方程②有x,y的值是方程组的解
D.适合方程①或方程②的x,y的值,一定是方程组的解
A
06
作业布置
【知识技能类作业】选做题:
06
作业布置
【知识技能类作业】选做题:
06
作业布置
【综合拓展类作业】
3. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”你能用二元一次方程组表示题中的数学关系吗?试找出问题的解.
06
作业布置
【综合拓展类作业】
x 20 21 22 23
y 15 14 13 12
2x+4y 100 98 96 94
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第二章 二元一次方程组
2.2二元一次方程组和它的解
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.理解并掌握二元一次方程组及其解的概念.
2.会用列表尝试的方法求二元一次方程组的解.
02
新知导入
1、判断下列各方程是不是二元一次方程?
√
×
×
2、下列各对数值中,是二元一次方程x-2y=7的解的是( )
B
A. B. C. D.
03
新知探究
每张成人票5元,每张儿童票3元.
昨天,我们8个人去红山公园玩,买门票花了34元.
到底去了几个成人,几个儿童呢?
03
新知探究
8个人去红山公园玩
,买门票花了34元.
每张成人票5元,每
张儿童票3元.
成人人数+儿童人数=8
成人票款+儿童票款=34
你能找出几个等量关系呢?
分析等量关系
03
新知讲解
成人人数+儿童人数=8
成人票款+儿童票款=34
列出方程
你能用数学符号将两个等式表示出来吗?
解:设成人的人数为x人,儿童的人数为y人
先想一想这两个式子的特点哟!
03
新知讲解
解:
x,y都分别表示同一个未知数,x,y的值必须同时满足以上两个方程.即
x+y=200,
y=x+10.
x+y=200,
y=x+10.
一个苹果和一个梨的质量合计200g(如图1),这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等(如图2).问苹果和梨的质量各为多少g?
如果设苹果和梨的质量分别为x(g)和y(g),你能列出几个方程?
观察 ,想一想它有什么特点?
x+y=200
y=x+10
共同点:
2.两个方程共含有两个未知数.
1.由两个一次方程组成;
3.等号两边都是整式.
03
新知讲解
1. 定义:由两个一次方程组成,并且含有两个未知数的方程组,叫做二元一次方程组.
2. 要点精析:
二元一次方程组的条件:
(1)共含有两个未知数.
(2)每个方程都是一次方程.
注:二元一次方程组并不要求每个方程都是二元的,如 2-x=2
2x+y=5 也是二元一次方程组.
03
新知讲解
一元一次方程与二元一次方程的相同点与不同点:
方程 不同点 相同点 一元一次方程 未知个数数1个 含有未知数项的次数1次
整式方程
二元一次方程 未知个数数2个 含有未知数项的次数1次 03
新知讲解
(1)已知方程 x+y=200,填写下表:
(2)已知方程 y=x+10,填写下表:
问题:有没有这样的解,它既是方程x+y=200的一个解,又是方程y=x+10的一个解
x … 85 90 95 100 105 …
y … …
115
110
100
95
95
105
x … 85 90 95 100 105 …
y … 105 …
95
100
110
115
95
105
03
新知讲解
同时满足二元一次方程组中各个方程的解叫作二元一次方程组的解.
二元一次方程组的解:
x=95
y=105
例如: 是 的解.
x+y=200
y=x+10
注意: 二元一次方程组的解也要用大括号表示
提炼概念
新课探究
例1
E
03
新知讲解
04
课堂练习
【知识技能类作业】必做题:
1.下列是二元一次方程组的是 ( )
A
04
课堂练习
【知识技能类作业】选做题:
04
课堂练习
【综合拓展类作业】
3.已知两个自然数的和是67,差是3设这两个自然数分别是x,y。请列出关于x,y的方程组,并用列表尝试的方法求出这两个自然数。
解:根据题意可列出方程组:{
x+y=67
x-y=3
分析:列表的时候要注意数据的选择。
x … 32 33 34 35 36 37 38 …
y … 29 30 31 32 34 35 36 …
x=y … …
61
63
65
67
70
72
74
05
课堂小结
1.二元一次方程组
定义:由两个_______次方程组成,并且含有______个未知数的方程组,叫做二元一次方程组.
2.二元一次方程组的解
定义:_________满足二元一次方程组中各个方程的解,叫做这个二元一次方程组的解.
一
两
同时
06
作业布置
【知识技能类作业】必做题:
A.同时适合方程①和方程②的x,y的值是方程组的解
B.适合方程①的x,y的值是方程组的解
C.适合方程②有x,y的值是方程组的解
D.适合方程①或方程②的x,y的值,一定是方程组的解
A
06
作业布置
【知识技能类作业】选做题:
06
作业布置
【知识技能类作业】选做题:
06
作业布置
【综合拓展类作业】
3. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?”你能用二元一次方程组表示题中的数学关系吗?试找出问题的解.
06
作业布置
【综合拓展类作业】
x 20 21 22 23
y 15 14 13 12
2x+4y 100 98 96 94
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
