3.3 多项式的乘法 (2) 课件(共19张PPT)
文档属性
| 名称 | 3.3 多项式的乘法 (2) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-08 17:20:18 | ||
图片预览




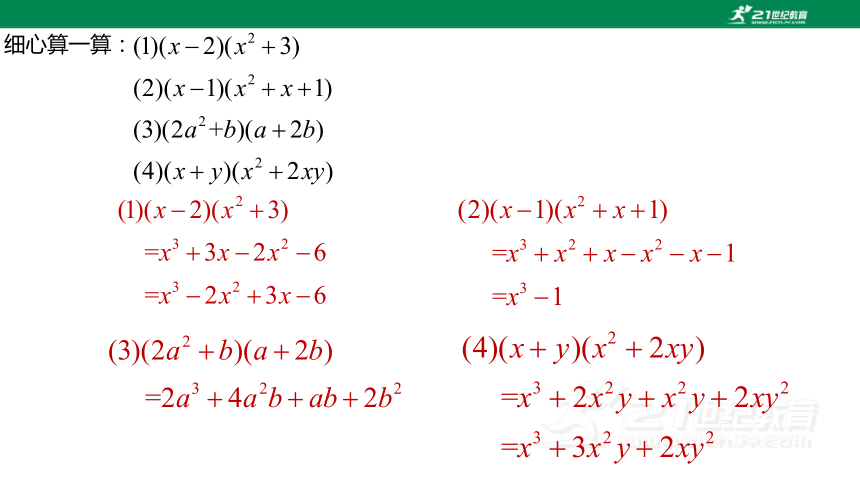

文档简介
(共19张PPT)
3.3 多项式的乘法(2)
浙教版七年级下册
3x3 + x2 -4x +8
3次
2次
1次
0次
1
按字母x的降幂排列:
8 -4x + x2 + 3x3
0次
1
1次
2次
3次
按字母x的升幂排列:
温故知新:
多项式 2x-x2+3,按字母x的降幂排列:
多项式 6y2+y-1+7y3,按字母y的升幂排列;
多项式7x2 - 3x-2x3-1,按字母x的降幂排列:
-x2+2x+3
-2x3+7x2-3x- 1.
-1+y+6y2+7y3
不含字母的项,若按降幂排列时,则排在最后一项;
若按升幂排列时,则排在最前面一项.
把多项式a2b+3ab2-2b3+a3按 a 的降幂排列是
,
a3+ a2 b +3 ab2-2 b3
a3+a2 b +3 ab2-2 b3
按 b 的升幂排列是 .
不含字母的项,若按降幂排列时,则排在最后一项;
若按升幂排列时,则排在最前面一项.
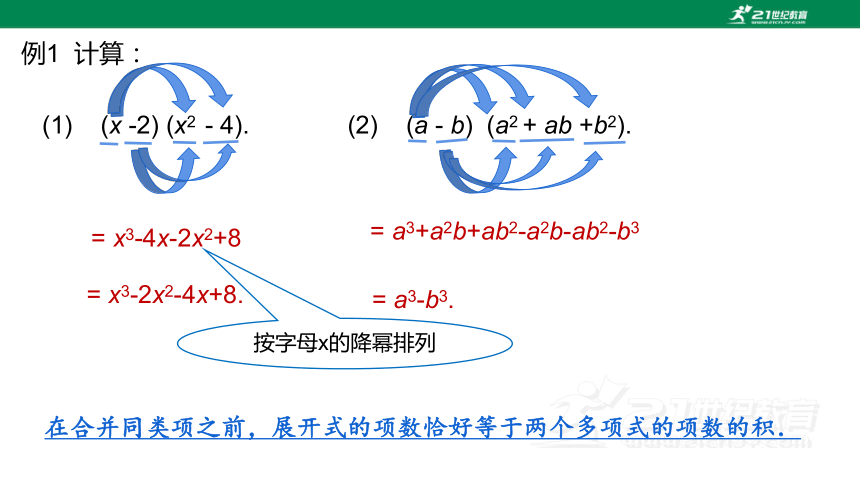
例1 计算:
(1) (x -2) (x2 - 4). (2) (a - b) (a2 + ab +b2).
= x3-4x-2x2+8
按字母x的降幂排列
= a3+a2b+ab2-a2b-ab2-b3
= x3-2x2-4x+8.
= a3-b3.
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
细心算一算:
例2 化简:ab(10a-3b)-(2a-b)(3ab-4a2).
这个代数式的值和a,b取值有关吗
解 ab (10a-3b) - (2a-b) (3ab-4a2)
因为这个代数式化简后只含字母a,
所以这个代数式的值只和字母 a的取值有关,和字母b的取值无关.
【 】
=10a2b-3ab2-6a2b+8a3+3ab2-4a2b
=8a3.
减数是多项式
多项式参与运算,添加括号( )
= 10a2b - 3ab2 - 6a2b - 8a3 - 3ab2+4a2b
【 】
化简: 3x(x2+2x+7) - (x2+7)(3x-5).
=3x3+6x2+21x-(3x3-5x2+21x-35)
=11x2+35
=3x3+6x2+21x-3x3+5x2-21x+35
【 】
例3 解方程:
解:两边去括号,得
合并同类项,得
化简,得
原方程的解为
运算要求:正确、灵活、合理、简洁
解下列方程
解:两边去括号得
合并同类项得
化简得
所以原方程的解为
【 】
1. 计算
夯实基础,稳扎稳打
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
当 s =-3 时,
原式=9+(-3)= 6
化简后的代数式只含字母 s,不含字母 t,故代数式的值与t无关.
解:能.
有序思考,不慌不忙;有序解答,不急不慢
=2x3-3x2+2x-2x2+3x-2-{(x2+x)(x-2)}
=2x3-3x2+2x-2x2+3x-2-{x3-2+-2x)}
=2x3-3x2+2x-2x2+3x-2-x3+2-+2x
=x3-4x2+7x-2
连续递推,豁然开朗
有序思考,不慌不忙;有序解答,不急不慢
2x2-5x-{(2x-2)(x+7)}=0
2x2-5x-{2x2+14x-2x-14}=0
2x2-5x-2x2-14x+2x+14=0
-17x+14=0
-17x=-14
x=
有序思考,不慌不忙;有序解答,不急不慢
(x+1) (y+1)(z+1)-xyz
=(xy+x+y+1)(z+1)-xyz
=xz+yz+z+xy+x+y+1
=xyz+xz+yz+z+xy+x+y+1-xyz
6.观察下列各式的计算结果与相乘的两个多项式之间的关系
.
你能总结出上面式子的规律吗?请尝试用数学语言表达.
能, (x+y)(x2-xy+y2)=x3+y3
x3+64
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.3 多项式的乘法(2)
浙教版七年级下册
3x3 + x2 -4x +8
3次
2次
1次
0次
1
按字母x的降幂排列:
8 -4x + x2 + 3x3
0次
1
1次
2次
3次
按字母x的升幂排列:
温故知新:
多项式 2x-x2+3,按字母x的降幂排列:
多项式 6y2+y-1+7y3,按字母y的升幂排列;
多项式7x2 - 3x-2x3-1,按字母x的降幂排列:
-x2+2x+3
-2x3+7x2-3x- 1.
-1+y+6y2+7y3
不含字母的项,若按降幂排列时,则排在最后一项;
若按升幂排列时,则排在最前面一项.
把多项式a2b+3ab2-2b3+a3按 a 的降幂排列是
,
a3+ a2 b +3 ab2-2 b3
a3+a2 b +3 ab2-2 b3
按 b 的升幂排列是 .
不含字母的项,若按降幂排列时,则排在最后一项;
若按升幂排列时,则排在最前面一项.
例1 计算:
(1) (x -2) (x2 - 4). (2) (a - b) (a2 + ab +b2).
= x3-4x-2x2+8
按字母x的降幂排列
= a3+a2b+ab2-a2b-ab2-b3
= x3-2x2-4x+8.
= a3-b3.
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
细心算一算:
例2 化简:ab(10a-3b)-(2a-b)(3ab-4a2).
这个代数式的值和a,b取值有关吗
解 ab (10a-3b) - (2a-b) (3ab-4a2)
因为这个代数式化简后只含字母a,
所以这个代数式的值只和字母 a的取值有关,和字母b的取值无关.
【 】
=10a2b-3ab2-6a2b+8a3+3ab2-4a2b
=8a3.
减数是多项式
多项式参与运算,添加括号( )
= 10a2b - 3ab2 - 6a2b - 8a3 - 3ab2+4a2b
【 】
化简: 3x(x2+2x+7) - (x2+7)(3x-5).
=3x3+6x2+21x-(3x3-5x2+21x-35)
=11x2+35
=3x3+6x2+21x-3x3+5x2-21x+35
【 】
例3 解方程:
解:两边去括号,得
合并同类项,得
化简,得
原方程的解为
运算要求:正确、灵活、合理、简洁
解下列方程
解:两边去括号得
合并同类项得
化简得
所以原方程的解为
【 】
1. 计算
夯实基础,稳扎稳打
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
当 s =-3 时,
原式=9+(-3)= 6
化简后的代数式只含字母 s,不含字母 t,故代数式的值与t无关.
解:能.
有序思考,不慌不忙;有序解答,不急不慢
=2x3-3x2+2x-2x2+3x-2-{(x2+x)(x-2)}
=2x3-3x2+2x-2x2+3x-2-{x3-2+-2x)}
=2x3-3x2+2x-2x2+3x-2-x3+2-+2x
=x3-4x2+7x-2
连续递推,豁然开朗
有序思考,不慌不忙;有序解答,不急不慢
2x2-5x-{(2x-2)(x+7)}=0
2x2-5x-{2x2+14x-2x-14}=0
2x2-5x-2x2-14x+2x+14=0
-17x+14=0
-17x=-14
x=
有序思考,不慌不忙;有序解答,不急不慢
(x+1) (y+1)(z+1)-xyz
=(xy+x+y+1)(z+1)-xyz
=xz+yz+z+xy+x+y+1
=xyz+xz+yz+z+xy+x+y+1-xyz
6.观察下列各式的计算结果与相乘的两个多项式之间的关系
.
你能总结出上面式子的规律吗?请尝试用数学语言表达.
能, (x+y)(x2-xy+y2)=x3+y3
x3+64
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
