3.4 乘法公式 (1) 课件(共25张PPT)
文档属性
| 名称 | 3.4 乘法公式 (1) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-10 12:36:13 | ||
图片预览







文档简介
(共25张PPT)
3.4 乘法公式(1)
浙教版七年级下册
多项式与多项式相乘:
(x + 2)( x+3)
=x2
+3x
+2x
+6
=x2
+5x
+6.
(a+b)(p+q)
=ap
+aq
+bp
+bq
温故知新:
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
多项式与多项式相乘的展开式
填一填
(x+1)(x–1) =
(2+m)(2–m) =
(2x+1)(2x–1) =
x2 – x + x –
=x2 –
22 – 2m + 2m – m2
(2x)2 – 2x + 2x –12
= – m2
=(2x)2 – 12
(x +1) ( x – 1) = x2 – 12
(2 +m) (2 – m) = 22 – m2
(2x+1) (2x – 1) = – 12
(a )(a )=
+b
– b
a2
– b2
两个数的和与这两个数的差的积,等于这两个数的平方差.
文字语言:
符号语言:
证明:
(a+b)(a –b)
=a2 –ab + ab – b2
=a2 – b2
平方差公式
多项式与多项式相乘的展开式:
这两个数的平方差,
结构特征①:
平方差公式
(a )(a )=
+b
– b
a2
– b2
“+、-” (1) 运算符号:加号、减号
运算要求:正确、灵活、合理、简洁
结构特征②:
相同项
符号相反项的平方
符号相同项的平方
相反项
平方差公式
(a )(a )=
+b
– b
a2
– b2
“+、-” (2) 性质符号:正号、负号
运算要求:正确、灵活、合理、简洁
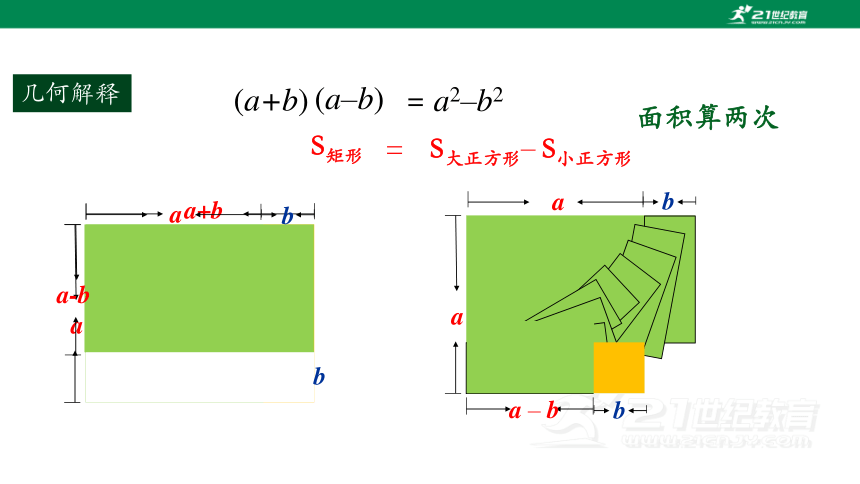
a
b
a+b
a-b
(a+b)
a2–b2
=
S矩形
a
a
a
b
几何解释
b
S大正方形– S小正方形
=
面积算两次
(a–b)
a – b
b
例1.运用平方差公式进行计算:
=(3x)2–(5y)2
= 9x2–25y2
步骤:1、判断;2、调整;
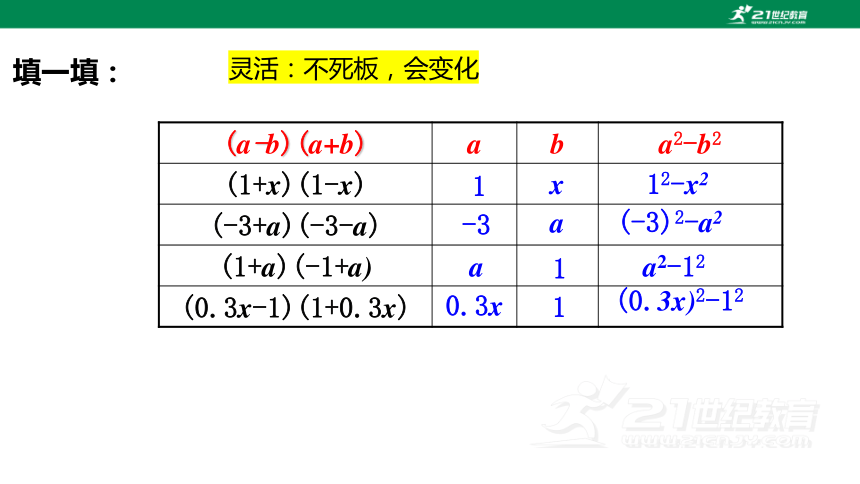
填一填:
(a-b)(a+b) a b a2-b2
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(0.3x)2-12
灵活:不死板,会变化
例2 用平方差公式计算:
解
运用平方差公式计算:
(1); (2).
=(2000+1)×(2000 1)
=
=4000000 1
=3999999
=(1000 2)×(1000+2)
=
=1000000 4
=999996.
简便计算
a
b
b
(a+b)
(a-b)
b
(a+b)
(a-b)
a
a
a
b
(a + b)(a b) =
a2 b2.
b
几何直观
归纳整理
(a+b) (a-b)=a2 -b2
平方差公式
符号语言
文字语言
两数和
与两数差=
这两数的平方差
观察公式,满足什么特征的多项式相乘,可用平方差公式呢?
左式特征:
右式结果:
(相同项)2-(相反项)2
1.运用平方差公式计算:
(1) (3x+2)(3x-2)
分析:在(1)中,可以把 3x 看成 a ,把 2 看成 b, 即
(3x+2)(3x-2)= ( 3x)2 - 22
(a+ b)(a - b) = a2 - b2
解:(1) (3x+2)(3x-2) = ( 3x)2 - 22 =9x2 -4
夯实基础,稳扎稳打
分析:在(2)中,可以把 -x 看成 a,把 2y 看成 b, 即
(-x+2y) (-x-2y) = ( -x)2 - ( 2y)2
(a+b) ( a - b) = a2 - b2
解:(2) (-x+2y)(-x-2y) = ( -x)2 - ( 2y)2 = x2 - 4y2
运用平方差公式计算:
(2) (-x+2y)(-x-2y).
(3) 102×98
=(100+2) ×(100-2)
=1002 - 22
=10000-4
=9996
=(50+0.5)(50-0.5)
=502-0.52
=2500-0.25
=2499.75;
(4)50.5×49.5
3:请用简便的方法计算
20222 – 2024×2020
20222 – 2024×2020
= 20222 –(2022+2)(2022–2)
= 20222 –(20222 – 22)
= 20222 – 20222+22
= 4
解:
×
连续递推,豁然开朗
4.计算:
( y+2)( y-2 ) - ( y-1 )( y+1 )
= y2 - 22 - ( y2-1)
= y2 - 4 - y2+1
= - 3
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
适当交换位置
5 运用平方差公式计算:
(1) (b+2a)(2a-b);
(2)(-a-b)(a-b)
=(-b)2-a2
=b2-a2
=(-b-a)(-b+a)
合理变形
紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用.
(3)(-2y-3x)(2y-3x)
=(-3x)2-(2y)2
=9x2-4y2
(4)(5a2+3b2)(-5a2+3b2)
=(3b2 )2-(5a2 )2
=9b4-25a4
随堂练习
=(-3x-2y)(-3x+2y)
= (3b2+5a2)(3b2-5a2)
6.利用平方差公式计算:
(1)(a-2)(a+2)(a2 + 4)
=(a2-4)(a2+4)
=a4-16.
(2) (x-y)(x+y)(x2+y2)(x4+y4).
=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
思维拓展,更上一层
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=(24-1)(24+1)(28+1)+1
=(28-1)(28+1)+1
=216-1+1
=216
(3)
给我最大快乐的,不是已懂得知识,而是不断的进步;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
——高斯
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4 乘法公式(1)
浙教版七年级下册
多项式与多项式相乘:
(x + 2)( x+3)
=x2
+3x
+2x
+6
=x2
+5x
+6.
(a+b)(p+q)
=ap
+aq
+bp
+bq
温故知新:
在合并同类项之前,展开式的项数恰好等于两个多项式的项数的积.
多项式与多项式相乘的展开式
填一填
(x+1)(x–1) =
(2+m)(2–m) =
(2x+1)(2x–1) =
x2 – x + x –
=x2 –
22 – 2m + 2m – m2
(2x)2 – 2x + 2x –12
= – m2
=(2x)2 – 12
(x +1) ( x – 1) = x2 – 12
(2 +m) (2 – m) = 22 – m2
(2x+1) (2x – 1) = – 12
(a )(a )=
+b
– b
a2
– b2
两个数的和与这两个数的差的积,等于这两个数的平方差.
文字语言:
符号语言:
证明:
(a+b)(a –b)
=a2 –ab + ab – b2
=a2 – b2
平方差公式
多项式与多项式相乘的展开式:
这两个数的平方差,
结构特征①:
平方差公式
(a )(a )=
+b
– b
a2
– b2
“+、-” (1) 运算符号:加号、减号
运算要求:正确、灵活、合理、简洁
结构特征②:
相同项
符号相反项的平方
符号相同项的平方
相反项
平方差公式
(a )(a )=
+b
– b
a2
– b2
“+、-” (2) 性质符号:正号、负号
运算要求:正确、灵活、合理、简洁
a
b
a+b
a-b
(a+b)
a2–b2
=
S矩形
a
a
a
b
几何解释
b
S大正方形– S小正方形
=
面积算两次
(a–b)
a – b
b
例1.运用平方差公式进行计算:
=(3x)2–(5y)2
= 9x2–25y2
步骤:1、判断;2、调整;
填一填:
(a-b)(a+b) a b a2-b2
(1+x)(1-x)
(-3+a)(-3-a)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
(0.3x)2-12
灵活:不死板,会变化
例2 用平方差公式计算:
解
运用平方差公式计算:
(1); (2).
=(2000+1)×(2000 1)
=
=4000000 1
=3999999
=(1000 2)×(1000+2)
=
=1000000 4
=999996.
简便计算
a
b
b
(a+b)
(a-b)
b
(a+b)
(a-b)
a
a
a
b
(a + b)(a b) =
a2 b2.
b
几何直观
归纳整理
(a+b) (a-b)=a2 -b2
平方差公式
符号语言
文字语言
两数和
与两数差=
这两数的平方差
观察公式,满足什么特征的多项式相乘,可用平方差公式呢?
左式特征:
右式结果:
(相同项)2-(相反项)2
1.运用平方差公式计算:
(1) (3x+2)(3x-2)
分析:在(1)中,可以把 3x 看成 a ,把 2 看成 b, 即
(3x+2)(3x-2)= ( 3x)2 - 22
(a+ b)(a - b) = a2 - b2
解:(1) (3x+2)(3x-2) = ( 3x)2 - 22 =9x2 -4
夯实基础,稳扎稳打
分析:在(2)中,可以把 -x 看成 a,把 2y 看成 b, 即
(-x+2y) (-x-2y) = ( -x)2 - ( 2y)2
(a+b) ( a - b) = a2 - b2
解:(2) (-x+2y)(-x-2y) = ( -x)2 - ( 2y)2 = x2 - 4y2
运用平方差公式计算:
(2) (-x+2y)(-x-2y).
(3) 102×98
=(100+2) ×(100-2)
=1002 - 22
=10000-4
=9996
=(50+0.5)(50-0.5)
=502-0.52
=2500-0.25
=2499.75;
(4)50.5×49.5
3:请用简便的方法计算
20222 – 2024×2020
20222 – 2024×2020
= 20222 –(2022+2)(2022–2)
= 20222 –(20222 – 22)
= 20222 – 20222+22
= 4
解:
×
连续递推,豁然开朗
4.计算:
( y+2)( y-2 ) - ( y-1 )( y+1 )
= y2 - 22 - ( y2-1)
= y2 - 4 - y2+1
= - 3
=(2a+b)(2a-b)
=(2a)2-b2
=4a2-b2.
适当交换位置
5 运用平方差公式计算:
(1) (b+2a)(2a-b);
(2)(-a-b)(a-b)
=(-b)2-a2
=b2-a2
=(-b-a)(-b+a)
合理变形
紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用.
(3)(-2y-3x)(2y-3x)
=(-3x)2-(2y)2
=9x2-4y2
(4)(5a2+3b2)(-5a2+3b2)
=(3b2 )2-(5a2 )2
=9b4-25a4
随堂练习
=(-3x-2y)(-3x+2y)
= (3b2+5a2)(3b2-5a2)
6.利用平方差公式计算:
(1)(a-2)(a+2)(a2 + 4)
=(a2-4)(a2+4)
=a4-16.
(2) (x-y)(x+y)(x2+y2)(x4+y4).
=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
思维拓展,更上一层
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=(24-1)(24+1)(28+1)+1
=(28-1)(28+1)+1
=216-1+1
=216
(3)
给我最大快乐的,不是已懂得知识,而是不断的进步;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。
——高斯
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
