1.2 同位角、内错角、同旁内角(含解析)-2024-2025学年浙教版七年级下册 同步分层作业
文档属性
| 名称 | 1.2 同位角、内错角、同旁内角(含解析)-2024-2025学年浙教版七年级下册 同步分层作业 |  | |
| 格式 | doc | ||
| 文件大小 | 833.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 15:05:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.2同位角、内错角、同旁内角 同步分层作业
1.下列四幅图中,∠1和∠2是同位角的是( )
A. B. C. D.
2.如图中,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如图,AB,CD被DE所截,则∠D的同旁内角是( )
A.∠1 B.∠2 C.∠3 D.∠4
4.下列说法中正确的有( )
①相等的角是对顶角;
②有公共顶点和一条公共边,且和为180°的两个角互为邻补角;
③同一平面内过一点有且只有一条直线与已知直线垂直;
④直线外一点到这条直线的垂线段,叫做点到直线的距离;
⑤如图,∠1和∠2是同旁内角.
A.0个 B.1个 C.2个 D.3个
5.如图,下列说法正确的是( )
A.∠2与∠B是同位角 B.∠1与∠4是内错角 C.∠2与∠3是同旁内角 D.∠4与∠A是内错角
6.如图,直线a,b被直线c所截,∠1的同位角是 .
7.如图,直线AB,CD被AE所截,则∠A的同旁内角是 .
8.如图,∠1和 是同位角,和 是内错角,∠3的邻补角是 .
9.如图,若∠2=100°,则∠1的同位角等于 度,∠1的内错角等于 度,∠1的同旁内角等于 度.
10.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
11.∠2与∠3是直线 、 被直线 所截得的 .(填序号)
(①AB,②AC,③DE,④BC,⑤DF,⑥同位角,⑦内错角,⑧同旁内角)
12.两条直线被第三条直线所截时,如果有一对同位角相等,则有内错角相等,同旁内角互补.请补充说理过程.
解:∵∠1=∠3,
∵∠1+∠2= °,(平角定义)
∴∠3+ =180°.( )
又∵∠3+∠4=180°,( )
∴∠2=∠4.( )
13.如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角;
(3)指出FB,BC被AC所截形成的同旁内角.
14.如图,下列结论中错误的是( )
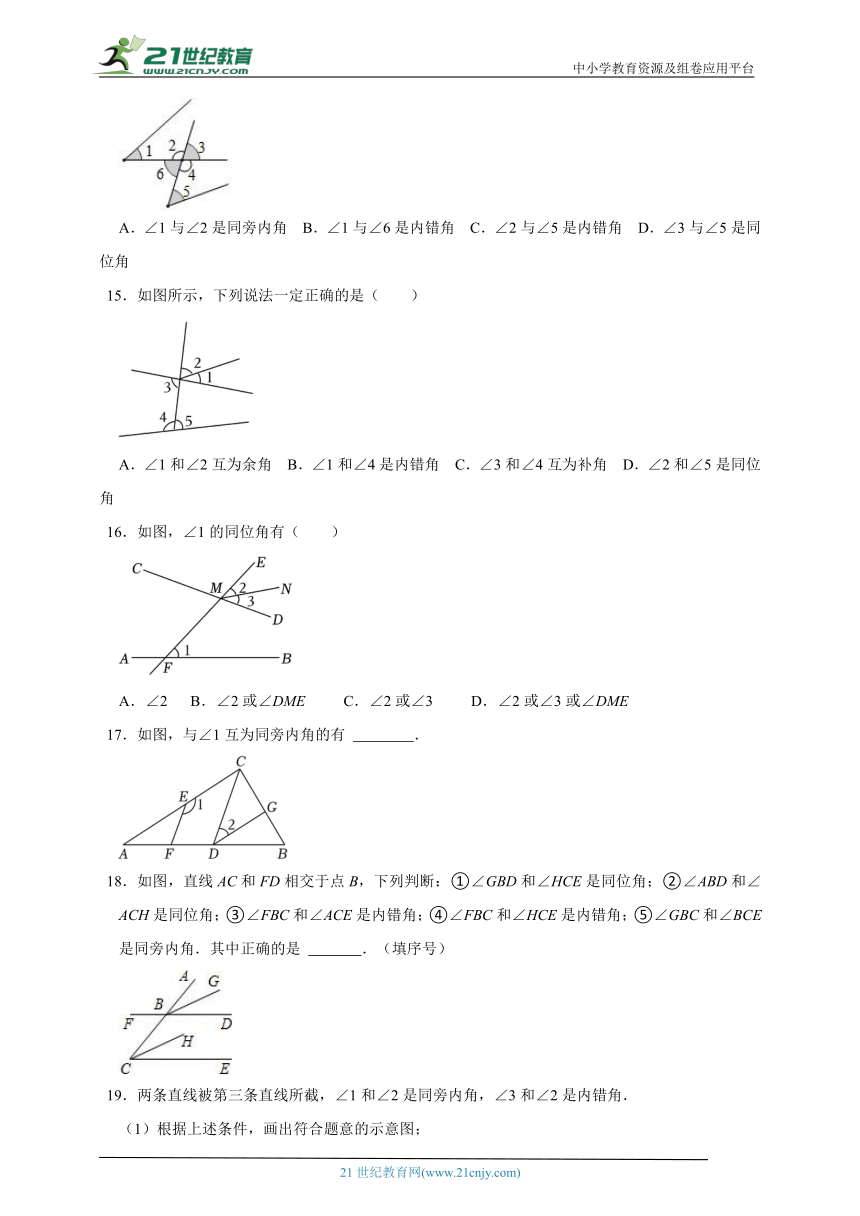
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角 C.∠2与∠5是内错角 D.∠3与∠5是同位角
15.如图所示,下列说法一定正确的是( )
A.∠1和∠2互为余角 B.∠1和∠4是内错角 C.∠3和∠4互为补角 D.∠2和∠5是同位角
16.如图,∠1的同位角有( )
A.∠2 B.∠2或∠DME C.∠2或∠3 D.∠2或∠3或∠DME
17.如图,与∠1互为同旁内角的有 .
18.如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是 .(填序号)
19.两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若∠1=3∠2、∠2=3∠3,求∠1,∠2的度数.
20.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
21.下列判断错误的是( )
A.∠2与∠4是同旁内角 B.∠3与∠4是内错角 C.∠5与∠6是同旁内角 D.∠1与∠5是同位角
22.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
23.如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出∠1的同旁内角与∠2的内错角;
(2)若测得∠AOE=65°,∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
答案与解析
1.下列四幅图中,∠1和∠2是同位角的是( )
A. B. C. D.
【点拨】根据同位角的特征,即可解答.
【解析】解:上列四幅图中,∠1和∠2是同位角的是
,
故选:B.
【点睛】本题考查了同位角、内错角、同旁内角,熟练掌握同位角、内错角、同旁内角的特征是解题的关键.
2.如图中,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【点拨】根据同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【解析】解:由同位角的定义可知,∠1的同位角是∠4.
故选:C.
【点睛】本题考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
3.如图,AB,CD被DE所截,则∠D的同旁内角是( )
A.∠1 B.∠2 C.∠3 D.∠4
【点拨】两条直线被第三条直线所截形成的角中,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可判断.
【解析】解:A、∠1与∠D是同位角,故A不符合题意;
B、∠2与∠D是同旁内角,故B符合题意;
C、∠3与∠D是内错角,故C不符合题意;
D、∠4与∠D不是同旁内角,故D不符合题意.
故选:B.
【点睛】本题考查同旁内角,关键是掌握同旁内角的定义.
4.下列说法中正确的有( )
①相等的角是对顶角;
②有公共顶点和一条公共边,且和为180°的两个角互为邻补角;
③同一平面内过一点有且只有一条直线与已知直线垂直;
④直线外一点到这条直线的垂线段,叫做点到直线的距离;
⑤如图,∠1和∠2是同旁内角.
A.0个 B.1个 C.2个 D.3个
【点拨】根据对顶角、邻补角,同位角、内错角、同旁内角以及垂线,点到直线的距离的定义逐项进行判断即可.
【解析】解:①对顶角相等,但相等的角不一定是对顶角,因此①不正确;
②有公共顶点和一条公共边,且和为180°的两个角不一定是互为邻补角;
如图:∠AOB=60°,∠AOC=120°,
此时∠AOB+∠AOC=180°,但不是邻补角,
因此②不正确;
③同一平面内过一点有且只有一条直线与已知直线垂直,因此③正确;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,因此④不正确;
⑤如图,∠1和∠2不是同旁内角,因此⑤不正确.
综上所述,正确的结论有③,共1个,
故选:B.
【点睛】本题考查对顶角、邻补角,同位角、内错角、同旁内角以及垂线,点到直线的距离,掌握对顶角、邻补角,同位角、内错角、同旁内角以及垂线,点到直线的距离的定义是正确解答的关键.
5.如图,下列说法正确的是( )
A.∠2与∠B是同位角 B.∠1与∠4是内错角 C.∠2与∠3是同旁内角 D.∠4与∠A是内错角
【点拨】根据同位角和同旁内角的定义解答即可.
【解析】解:A.∠2与∠B是同位角,该说法正确,故该选项符合题意;
B.∠1与∠4是同旁内角,原说法错误,故该选项不符合题意;
C.∠2与∠3是同位角,原说法错误,故该选项不符合题意;
D.∠4与∠A是同旁内角,原说法错误,故该选项不符合题意;
故选:A.
【点睛】本题考查了同位角、内错角、同旁内角的概念,两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
6.如图,直线a,b被直线c所截,∠1的同位角是 ∠4 .
【点拨】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,由此即可判断.
【解析】解:直线a,b被直线c所截,∠1的同位角是∠4.
故答案为:∠4.
【点睛】本题考查同位角,关键是掌握同位角的定义.
7.如图,直线AB,CD被AE所截,则∠A的同旁内角是 ∠AOC .
【点拨】根据同旁内角的定义即可求得.
【解析】解:∵直线AB,CD被AE所截,
∴∠A的同旁内角是∠AOC.
故答案为:∠AOC.
【点睛】本题主要考查同旁内角的定义,解决此题的关键是熟记同旁内角的定义.
8.如图,∠1和 ∠3 是同位角,和 ∠5 是内错角,∠3的邻补角是 ∠2或∠4 .
【点拨】根据同位角,内错角,邻补角的定义进行作答即可.
【解析】解:由题意知,∠1和∠3是同位角,和∠5是内错角,∠3的邻补角是∠2或∠4,
故答案为:∠3,∠5,∠2或∠4.
【点睛】本题考查了同位角,内错角,邻补角.熟练掌握同位角,内错角,邻补角是解题的关键.
9.如图,若∠2=100°,则∠1的同位角等于 80 度,∠1的内错角等于 80 度,∠1的同旁内角等于 100 度.
【点拨】在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
【解析】解:∵∠2=100°,
∴∠1的同位角=∠3=180°﹣∠2=180°﹣100°=80°,
∠1的内错角=∠5=180°﹣∠2=180°﹣100°=80°,
∠1的同旁内角=∠4=∠2=100°.
故答案为:80°;80°;100°.
【点睛】本题考查了同位角、同旁内角和内错角,掌握同位角、同旁内角和内错角的定义是关键.
10.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 80° ,∠3的内错角等于 80° ,∠3的同旁内角等于 100° .
【点拨】利用同位角,内错角,同旁内角的定义判断即可.
【解析】解:如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于80°,∠3的内错角等于80°,∠3的同旁内角等于100°,
故答案为:80°;80°;100°
【点睛】此题考查了同位角、内错角、同旁内角,熟练掌握各自的定义是解本题的关键.
11.∠2与∠3是直线 ③ 、 ④ 被直线 ⑤ 所截得的 ⑦ .(填序号)
(①AB,②AC,③DE,④BC,⑤DF,⑥同位角,⑦内错角,⑧同旁内角)
【点拨】根据内错角的概念求解即可.
【解析】解:∠2与∠3是直线DE、BC被直线DF所截得的内错角.
故答案为:③,④,⑤,⑦.
【点睛】本题考查了“三线八角”,熟练掌握同位角、内错角、同旁内角的图形特征是解题的关键.
12.两条直线被第三条直线所截时,如果有一对同位角相等,则有内错角相等,同旁内角互补.请补充说理过程.
解:∵∠1=∠3,
∵∠1+∠2= 180 °,(平角定义)
∴∠3+ ∠2 =180°.( 等量代换 )
又∵∠3+∠4=180°,( 平角定义 )
∴∠2=∠4.( 等量代换 )
【点拨】分别根据平角定义和等量代换即可得出答案.
【解析】解:∵∠1=∠3,
∵∠1+∠2=180°,(平角定义)
∴∠3+∠2=180°.(等量代换)
又∵∠3+∠4=180°,(平角定义)
∴∠2=∠4.(等量代换).
故答案为:180,∠2,等量代换,平角定义,等量代换.
【点睛】此题考查了同位角、内错角、同旁内角,关键是掌握同位角、内错角、同旁内角的定义.
13.如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角;
(3)指出FB,BC被AC所截形成的同旁内角.
【点拨】(1)两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,据此求解即可;
(2)根据内错角的定义求解即可;
(3)根据同旁内角的定义求解即可.
【解析】解:(1)同位角:∠FAE和∠B;内错角:∠B和∠DAB;同旁内角:∠EAB和∠B;
(2)解:∠EAC和∠BCA,∠DAC和∠ACG都是内错角;
(3)解:∠BAC和∠BCA,∠FAC和∠ACG都是同旁内角.
【点睛】此题主要考查了三线八角,关键是掌握同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
14.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角 C.∠2与∠5是内错角 D.∠3与∠5是同位角
【点拨】直接利用同旁内角以及内错角、同位角的定义分别判断得出答案.
【解析】解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5不是内错角,故C错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
【点睛】此题主要考查了同旁内角以及内错角、同位角的定义,正确掌握相关定义是解题关键.
15.如图所示,下列说法一定正确的是( )
A.∠1和∠2互为余角 B.∠1和∠4是内错角 C.∠3和∠4互为补角 D.∠2和∠5是同位角
【点拨】根据互为余角、互为补角、内错角、同位角以及同旁内角的定义结合具体图形进行判断即可.
【解析】解:A.由于∠1与∠2的和不一定是90°,所以∠1和∠2不一定是互为余角,因此选项A不符合题意;
B.∠1和∠4不是两条直线被第三条直线所截得的角,不符合内错角的定义,因此选项B不符合题意;
C.∠3和∠4是一组同旁内角,但∠3和∠4不一定互补,因此选项C不符合题意;
D.∠2和∠5是两条直线被第三条直线所截的同位角,因此选项D符合题意.
故选:D.
【点睛】本题考查互为余角、互为补角、内错角、同位角以及同旁内角,掌握互为余角、互为补角、内错角、同位角以及同旁内角的定义是正确解答的关键.
16.如图,∠1的同位角有( )
A.∠2 B.∠2或∠DME C.∠2或∠3 D.∠2或∠3或∠DME
【点拨】要弄清哪一条直线是截线,哪两条直线是被截线即可求解.
【解析】解:∠2是∠1的同位角,∠3不是∠1的同位角,∠DME是∠1的同位角.
故选:B.
【点睛】此题主要考查在复杂的图形中识别同位角,准确识别同位角,弄清哪两条直线被哪一条线所截即可求解.
17.如图,与∠1互为同旁内角的有 ∠EFD、∠ECD和∠ECB .
【点拨】本题考查三线八角,根据同旁内角的特点,进行判断即可.
【解析】解:由图可知:与∠1互为同旁内角的有∠EFD,∠ECD,∠ECB;
故答案为:∠EFD、∠ECD和∠ECB.
【点睛】本题考查三线八角,属于简单题.
18.如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是 ②③⑤ .(填序号)
【点拨】同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.根据同位角、同旁内角、内错角的特征进行判断.
【解析】解:①∠GBD和∠HCE不符合同位角的定义,故本选项错误;
②∠ABD和∠ACH是同位角,故本选项正确;
③∠FBC和∠ACE是内错角,故本选项正确;
④∠FBC和∠HCE不符合内错角的定义,故本选项错误;
⑤∠GBC和∠BCE是同旁内角,故本选项正确.
故答案为:②③⑤.
【点睛】本题考查了同位角、同旁内角、内错角的定义,正确且熟练掌握同位角、同旁内角、内错角的定义和形状,是解题的关键.
19.两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若∠1=3∠2、∠2=3∠3,求∠1,∠2的度数.
【点拨】(1)根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,画出图形.
(2)根据已知角的关系确定∠1=9∠3,再根据图形中∠1和∠3组成邻补角互补可得方程,再解即可.
【解析】解:(1)如图所示:
(2)∵∠1=3∠2、∠2=3∠3,
∴∠1=9∠3,
∵∠1+∠3=180°,
∴9∠3+∠3=180°,
∴∠3=18°,
∴∠1=162°,∠2=54°.
【点睛】此题主要考查了三线八角,以及角的计算,关键是掌握内错角的边构成“Z“形,同旁内角的边构成“U”形.
20.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
【点拨】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,若两个角都在两直线之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可判断.
【解析】解:①②③中的判断正确,故①②③符合题意;
④、∠1与∠3不是同位角,故④不符合题意.
故选:A.
【点睛】本题考查同位角,内错角,同旁内角,关键是掌握同位角,内错角,同旁内角的定义.
21.下列判断错误的是( )
A.∠2与∠4是同旁内角 B.∠3与∠4是内错角 C.∠5与∠6是同旁内角 D.∠1与∠5是同位角
【点拨】根据同位角、内错角、同旁内角的定义进行解答即可.
【解析】解:A、∠2与∠4是同旁内角,原说法正确,故此选项不符合题意;
B、∠3与∠4是内错角,原说法正确,故此选项不符合题意;
C、∠5与∠6不是同旁内角,原说法错误,故此选项符合题意;
D、∠1与∠5是同位角,原说法正确,故此选项不符合题意.
故选:C.
【点睛】此题主要考查了同位角、内错角、同旁内角,解题的关键是熟记同位角、内错角、同旁内角的定义.
22.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
【点拨】(1)路径:∠1→∠12→∠8;
(2)路径:∠1→∠10→∠5→∠8.
【解析】解:(1)路径∠1∠12∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:
路径:∠1∠10∠5∠8.
【点睛】考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
23.如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出∠1的同旁内角与∠2的内错角;
(2)若测得∠AOE=65°,∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
【点拨】(1)两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可得到答案;
(2)由邻补角的性质求出∠AOM的度数,由∠MOE=∠AOE﹣∠AOM,即可得到答案.
【解析】解:(1)∠1的同旁内角是∠MOE,∠AOE,∠ADE,∠2的内错角是∠MOE,∠AOE;
(2)∵∠BOM=145°,
∴∠AOM=180°﹣∠BOM=35°,
∴∠MOE=∠AOE﹣∠AOM=65°﹣35°=30°,
∴水下部分向上折弯了30度.
【点睛】本题考查同旁内角,内错角,角的计算,关键是掌握同旁内角,内错角的定义,邻补角的性质.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
1.2同位角、内错角、同旁内角 同步分层作业
1.下列四幅图中,∠1和∠2是同位角的是( )
A. B. C. D.
2.如图中,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
3.如图,AB,CD被DE所截,则∠D的同旁内角是( )
A.∠1 B.∠2 C.∠3 D.∠4
4.下列说法中正确的有( )
①相等的角是对顶角;
②有公共顶点和一条公共边,且和为180°的两个角互为邻补角;
③同一平面内过一点有且只有一条直线与已知直线垂直;
④直线外一点到这条直线的垂线段,叫做点到直线的距离;
⑤如图,∠1和∠2是同旁内角.
A.0个 B.1个 C.2个 D.3个
5.如图,下列说法正确的是( )
A.∠2与∠B是同位角 B.∠1与∠4是内错角 C.∠2与∠3是同旁内角 D.∠4与∠A是内错角
6.如图,直线a,b被直线c所截,∠1的同位角是 .
7.如图,直线AB,CD被AE所截,则∠A的同旁内角是 .
8.如图,∠1和 是同位角,和 是内错角,∠3的邻补角是 .
9.如图,若∠2=100°,则∠1的同位角等于 度,∠1的内错角等于 度,∠1的同旁内角等于 度.
10.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
11.∠2与∠3是直线 、 被直线 所截得的 .(填序号)
(①AB,②AC,③DE,④BC,⑤DF,⑥同位角,⑦内错角,⑧同旁内角)
12.两条直线被第三条直线所截时,如果有一对同位角相等,则有内错角相等,同旁内角互补.请补充说理过程.
解:∵∠1=∠3,
∵∠1+∠2= °,(平角定义)
∴∠3+ =180°.( )
又∵∠3+∠4=180°,( )
∴∠2=∠4.( )
13.如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角;
(3)指出FB,BC被AC所截形成的同旁内角.
14.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角 C.∠2与∠5是内错角 D.∠3与∠5是同位角
15.如图所示,下列说法一定正确的是( )
A.∠1和∠2互为余角 B.∠1和∠4是内错角 C.∠3和∠4互为补角 D.∠2和∠5是同位角
16.如图,∠1的同位角有( )
A.∠2 B.∠2或∠DME C.∠2或∠3 D.∠2或∠3或∠DME
17.如图,与∠1互为同旁内角的有 .
18.如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是 .(填序号)
19.两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若∠1=3∠2、∠2=3∠3,求∠1,∠2的度数.
20.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
21.下列判断错误的是( )
A.∠2与∠4是同旁内角 B.∠3与∠4是内错角 C.∠5与∠6是同旁内角 D.∠1与∠5是同位角
22.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
23.如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出∠1的同旁内角与∠2的内错角;
(2)若测得∠AOE=65°,∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
答案与解析
1.下列四幅图中,∠1和∠2是同位角的是( )
A. B. C. D.
【点拨】根据同位角的特征,即可解答.
【解析】解:上列四幅图中,∠1和∠2是同位角的是
,
故选:B.
【点睛】本题考查了同位角、内错角、同旁内角,熟练掌握同位角、内错角、同旁内角的特征是解题的关键.
2.如图中,∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【点拨】根据同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【解析】解:由同位角的定义可知,∠1的同位角是∠4.
故选:C.
【点睛】本题考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
3.如图,AB,CD被DE所截,则∠D的同旁内角是( )
A.∠1 B.∠2 C.∠3 D.∠4
【点拨】两条直线被第三条直线所截形成的角中,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可判断.
【解析】解:A、∠1与∠D是同位角,故A不符合题意;
B、∠2与∠D是同旁内角,故B符合题意;
C、∠3与∠D是内错角,故C不符合题意;
D、∠4与∠D不是同旁内角,故D不符合题意.
故选:B.
【点睛】本题考查同旁内角,关键是掌握同旁内角的定义.
4.下列说法中正确的有( )
①相等的角是对顶角;
②有公共顶点和一条公共边,且和为180°的两个角互为邻补角;
③同一平面内过一点有且只有一条直线与已知直线垂直;
④直线外一点到这条直线的垂线段,叫做点到直线的距离;
⑤如图,∠1和∠2是同旁内角.
A.0个 B.1个 C.2个 D.3个
【点拨】根据对顶角、邻补角,同位角、内错角、同旁内角以及垂线,点到直线的距离的定义逐项进行判断即可.
【解析】解:①对顶角相等,但相等的角不一定是对顶角,因此①不正确;
②有公共顶点和一条公共边,且和为180°的两个角不一定是互为邻补角;
如图:∠AOB=60°,∠AOC=120°,
此时∠AOB+∠AOC=180°,但不是邻补角,
因此②不正确;
③同一平面内过一点有且只有一条直线与已知直线垂直,因此③正确;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,因此④不正确;
⑤如图,∠1和∠2不是同旁内角,因此⑤不正确.
综上所述,正确的结论有③,共1个,
故选:B.
【点睛】本题考查对顶角、邻补角,同位角、内错角、同旁内角以及垂线,点到直线的距离,掌握对顶角、邻补角,同位角、内错角、同旁内角以及垂线,点到直线的距离的定义是正确解答的关键.
5.如图,下列说法正确的是( )
A.∠2与∠B是同位角 B.∠1与∠4是内错角 C.∠2与∠3是同旁内角 D.∠4与∠A是内错角
【点拨】根据同位角和同旁内角的定义解答即可.
【解析】解:A.∠2与∠B是同位角,该说法正确,故该选项符合题意;
B.∠1与∠4是同旁内角,原说法错误,故该选项不符合题意;
C.∠2与∠3是同位角,原说法错误,故该选项不符合题意;
D.∠4与∠A是同旁内角,原说法错误,故该选项不符合题意;
故选:A.
【点睛】本题考查了同位角、内错角、同旁内角的概念,两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.
6.如图,直线a,b被直线c所截,∠1的同位角是 ∠4 .
【点拨】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,由此即可判断.
【解析】解:直线a,b被直线c所截,∠1的同位角是∠4.
故答案为:∠4.
【点睛】本题考查同位角,关键是掌握同位角的定义.
7.如图,直线AB,CD被AE所截,则∠A的同旁内角是 ∠AOC .
【点拨】根据同旁内角的定义即可求得.
【解析】解:∵直线AB,CD被AE所截,
∴∠A的同旁内角是∠AOC.
故答案为:∠AOC.
【点睛】本题主要考查同旁内角的定义,解决此题的关键是熟记同旁内角的定义.
8.如图,∠1和 ∠3 是同位角,和 ∠5 是内错角,∠3的邻补角是 ∠2或∠4 .
【点拨】根据同位角,内错角,邻补角的定义进行作答即可.
【解析】解:由题意知,∠1和∠3是同位角,和∠5是内错角,∠3的邻补角是∠2或∠4,
故答案为:∠3,∠5,∠2或∠4.
【点睛】本题考查了同位角,内错角,邻补角.熟练掌握同位角,内错角,邻补角是解题的关键.
9.如图,若∠2=100°,则∠1的同位角等于 80 度,∠1的内错角等于 80 度,∠1的同旁内角等于 100 度.
【点拨】在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系.
【解析】解:∵∠2=100°,
∴∠1的同位角=∠3=180°﹣∠2=180°﹣100°=80°,
∠1的内错角=∠5=180°﹣∠2=180°﹣100°=80°,
∠1的同旁内角=∠4=∠2=100°.
故答案为:80°;80°;100°.
【点睛】本题考查了同位角、同旁内角和内错角,掌握同位角、同旁内角和内错角的定义是关键.
10.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 80° ,∠3的内错角等于 80° ,∠3的同旁内角等于 100° .
【点拨】利用同位角,内错角,同旁内角的定义判断即可.
【解析】解:如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于80°,∠3的内错角等于80°,∠3的同旁内角等于100°,
故答案为:80°;80°;100°
【点睛】此题考查了同位角、内错角、同旁内角,熟练掌握各自的定义是解本题的关键.
11.∠2与∠3是直线 ③ 、 ④ 被直线 ⑤ 所截得的 ⑦ .(填序号)
(①AB,②AC,③DE,④BC,⑤DF,⑥同位角,⑦内错角,⑧同旁内角)
【点拨】根据内错角的概念求解即可.
【解析】解:∠2与∠3是直线DE、BC被直线DF所截得的内错角.
故答案为:③,④,⑤,⑦.
【点睛】本题考查了“三线八角”,熟练掌握同位角、内错角、同旁内角的图形特征是解题的关键.
12.两条直线被第三条直线所截时,如果有一对同位角相等,则有内错角相等,同旁内角互补.请补充说理过程.
解:∵∠1=∠3,
∵∠1+∠2= 180 °,(平角定义)
∴∠3+ ∠2 =180°.( 等量代换 )
又∵∠3+∠4=180°,( 平角定义 )
∴∠2=∠4.( 等量代换 )
【点拨】分别根据平角定义和等量代换即可得出答案.
【解析】解:∵∠1=∠3,
∵∠1+∠2=180°,(平角定义)
∴∠3+∠2=180°.(等量代换)
又∵∠3+∠4=180°,(平角定义)
∴∠2=∠4.(等量代换).
故答案为:180,∠2,等量代换,平角定义,等量代换.
【点睛】此题考查了同位角、内错角、同旁内角,关键是掌握同位角、内错角、同旁内角的定义.
13.如图,BF,DE相交于点A,BG交BF于点B,交AC于点C.
(1)指出DE,BC被BF所截形成的同位角、内错角、同旁内角;
(2)指出DE,BC被AC所截形成的内错角;
(3)指出FB,BC被AC所截形成的同旁内角.
【点拨】(1)两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,据此求解即可;
(2)根据内错角的定义求解即可;
(3)根据同旁内角的定义求解即可.
【解析】解:(1)同位角:∠FAE和∠B;内错角:∠B和∠DAB;同旁内角:∠EAB和∠B;
(2)解:∠EAC和∠BCA,∠DAC和∠ACG都是内错角;
(3)解:∠BAC和∠BCA,∠FAC和∠ACG都是同旁内角.
【点睛】此题主要考查了三线八角,关键是掌握同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
14.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角 C.∠2与∠5是内错角 D.∠3与∠5是同位角
【点拨】直接利用同旁内角以及内错角、同位角的定义分别判断得出答案.
【解析】解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5不是内错角,故C错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
【点睛】此题主要考查了同旁内角以及内错角、同位角的定义,正确掌握相关定义是解题关键.
15.如图所示,下列说法一定正确的是( )
A.∠1和∠2互为余角 B.∠1和∠4是内错角 C.∠3和∠4互为补角 D.∠2和∠5是同位角
【点拨】根据互为余角、互为补角、内错角、同位角以及同旁内角的定义结合具体图形进行判断即可.
【解析】解:A.由于∠1与∠2的和不一定是90°,所以∠1和∠2不一定是互为余角,因此选项A不符合题意;
B.∠1和∠4不是两条直线被第三条直线所截得的角,不符合内错角的定义,因此选项B不符合题意;
C.∠3和∠4是一组同旁内角,但∠3和∠4不一定互补,因此选项C不符合题意;
D.∠2和∠5是两条直线被第三条直线所截的同位角,因此选项D符合题意.
故选:D.
【点睛】本题考查互为余角、互为补角、内错角、同位角以及同旁内角,掌握互为余角、互为补角、内错角、同位角以及同旁内角的定义是正确解答的关键.
16.如图,∠1的同位角有( )
A.∠2 B.∠2或∠DME C.∠2或∠3 D.∠2或∠3或∠DME
【点拨】要弄清哪一条直线是截线,哪两条直线是被截线即可求解.
【解析】解:∠2是∠1的同位角,∠3不是∠1的同位角,∠DME是∠1的同位角.
故选:B.
【点睛】此题主要考查在复杂的图形中识别同位角,准确识别同位角,弄清哪两条直线被哪一条线所截即可求解.
17.如图,与∠1互为同旁内角的有 ∠EFD、∠ECD和∠ECB .
【点拨】本题考查三线八角,根据同旁内角的特点,进行判断即可.
【解析】解:由图可知:与∠1互为同旁内角的有∠EFD,∠ECD,∠ECB;
故答案为:∠EFD、∠ECD和∠ECB.
【点睛】本题考查三线八角,属于简单题.
18.如图,直线AC和FD相交于点B,下列判断:①∠GBD和∠HCE是同位角;②∠ABD和∠ACH是同位角;③∠FBC和∠ACE是内错角;④∠FBC和∠HCE是内错角;⑤∠GBC和∠BCE是同旁内角.其中正确的是 ②③⑤ .(填序号)
【点拨】同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.根据同位角、同旁内角、内错角的特征进行判断.
【解析】解:①∠GBD和∠HCE不符合同位角的定义,故本选项错误;
②∠ABD和∠ACH是同位角,故本选项正确;
③∠FBC和∠ACE是内错角,故本选项正确;
④∠FBC和∠HCE不符合内错角的定义,故本选项错误;
⑤∠GBC和∠BCE是同旁内角,故本选项正确.
故答案为:②③⑤.
【点睛】本题考查了同位角、同旁内角、内错角的定义,正确且熟练掌握同位角、同旁内角、内错角的定义和形状,是解题的关键.
19.两条直线被第三条直线所截,∠1和∠2是同旁内角,∠3和∠2是内错角.
(1)根据上述条件,画出符合题意的示意图;
(2)若∠1=3∠2、∠2=3∠3,求∠1,∠2的度数.
【点拨】(1)根据内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.
同旁内角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,画出图形.
(2)根据已知角的关系确定∠1=9∠3,再根据图形中∠1和∠3组成邻补角互补可得方程,再解即可.
【解析】解:(1)如图所示:
(2)∵∠1=3∠2、∠2=3∠3,
∴∠1=9∠3,
∵∠1+∠3=180°,
∴9∠3+∠3=180°,
∴∠3=18°,
∴∠1=162°,∠2=54°.
【点睛】此题主要考查了三线八角,以及角的计算,关键是掌握内错角的边构成“Z“形,同旁内角的边构成“U”形.
20.如图,下列判断:①∠A与∠1是同位角;②∠A与∠B是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
【点拨】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角,若两个角都在两直线之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,若两个角都在两直线之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可判断.
【解析】解:①②③中的判断正确,故①②③符合题意;
④、∠1与∠3不是同位角,故④不符合题意.
故选:A.
【点睛】本题考查同位角,内错角,同旁内角,关键是掌握同位角,内错角,同旁内角的定义.
21.下列判断错误的是( )
A.∠2与∠4是同旁内角 B.∠3与∠4是内错角 C.∠5与∠6是同旁内角 D.∠1与∠5是同位角
【点拨】根据同位角、内错角、同旁内角的定义进行解答即可.
【解析】解:A、∠2与∠4是同旁内角,原说法正确,故此选项不符合题意;
B、∠3与∠4是内错角,原说法正确,故此选项不符合题意;
C、∠5与∠6不是同旁内角,原说法错误,故此选项符合题意;
D、∠1与∠5是同位角,原说法正确,故此选项不符合题意.
故选:C.
【点睛】此题主要考查了同位角、内错角、同旁内角,解题的关键是熟记同位角、内错角、同旁内角的定义.
22.已知:如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上,例如:从起始位置∠1跳到终点位置∠3写出其中两种不同路径,路径1:∠1﹣同旁内角→∠9﹣内错角→∠3.
路径2:∠1一内错角→∠12一内错角→∠6﹣同位角→∠10﹣同旁内角→∠3.
试一试:(1)从起始∠1跳到终点角∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8?
【点拨】(1)路径:∠1→∠12→∠8;
(2)路径:∠1→∠10→∠5→∠8.
【解析】解:(1)路径∠1∠12∠8;
(2)从起始角∠1依次按同位角、内错角、同旁内角的顺序跳,能跳到终点∠8.其路径为:
路径:∠1∠10∠5∠8.
【点睛】考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.
23.如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变.
(1)请指出∠1的同旁内角与∠2的内错角;
(2)若测得∠AOE=65°,∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上折弯了多少度?请说明理由.
【点拨】(1)两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角,由此即可得到答案;
(2)由邻补角的性质求出∠AOM的度数,由∠MOE=∠AOE﹣∠AOM,即可得到答案.
【解析】解:(1)∠1的同旁内角是∠MOE,∠AOE,∠ADE,∠2的内错角是∠MOE,∠AOE;
(2)∵∠BOM=145°,
∴∠AOM=180°﹣∠BOM=35°,
∴∠MOE=∠AOE﹣∠AOM=65°﹣35°=30°,
∴水下部分向上折弯了30度.
【点睛】本题考查同旁内角,内错角,角的计算,关键是掌握同旁内角,内错角的定义,邻补角的性质.
基础过关
能力提升
培优拔尖
基础过关
能力提升
培优拔尖
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
