3.4 乘法公式 (2) 课件(共24张PPT)
文档属性
| 名称 | 3.4 乘法公式 (2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-12 15:07:10 | ||
图片预览





文档简介
(共24张PPT)
3.4 乘法公式(2)
浙教版七年级下册
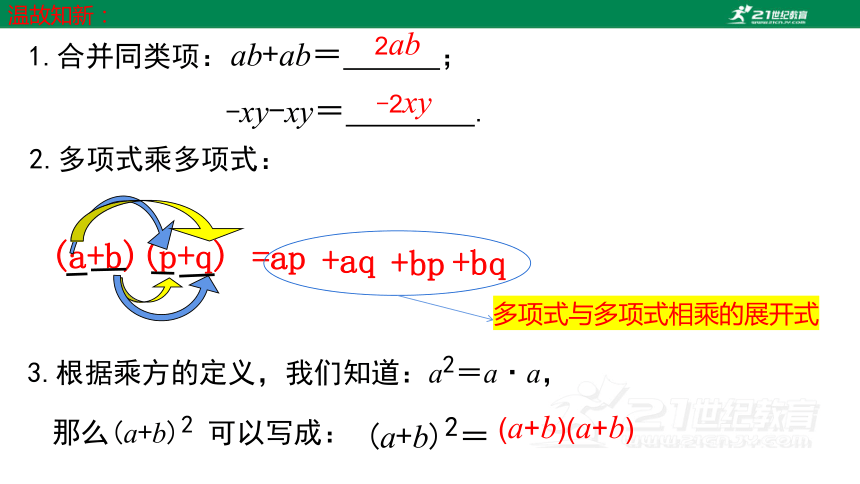
1.合并同类项:
温故知新:
-xy-xy= .
ab+ab= ;
2ab
-2xy
2.多项式乘多项式:
(a+b)(p+q)
=ap
+aq
+bp
+bq
多项式与多项式相乘的展开式
3.根据乘方的定义,我们知道:a2=a·a,
那么(a+b)2 可以写成:
(a+b)2=
(a+b)(a+b)
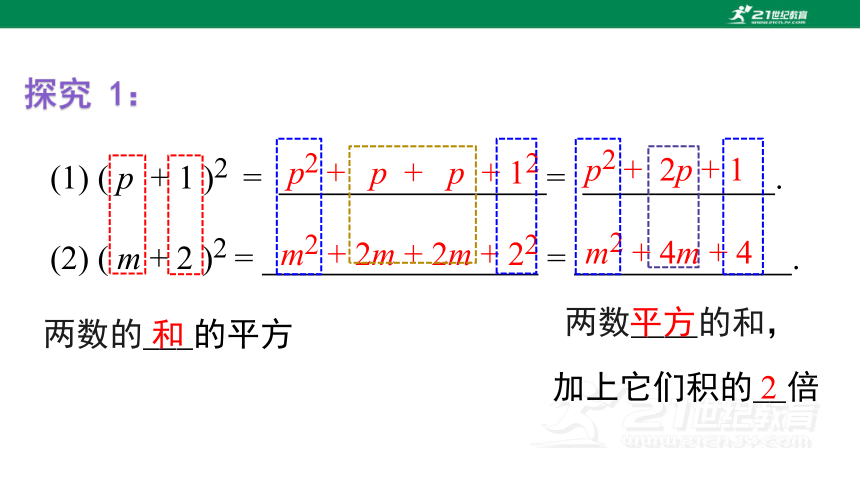
(1) ( p + 1 )2 = = .
探究 1:
(2) ( m + 2 )2 = = .
p2 + p + p + 12
m2 + 2m + 2m + 22
两数的___的平方
和
两数____的和,
平方
加上它们积的__倍
2
p2 + 2p + 1
m2 + 4m + 4
规律:两个数和的平方,等于这两个数的平方的和,
加上这两个数积的2倍.
∵(a+b)2 = (a+b)(a+b)
= a2+2ab+b2.
= a2 + ab + ab + b2
思路一:
代数推理
几何推理
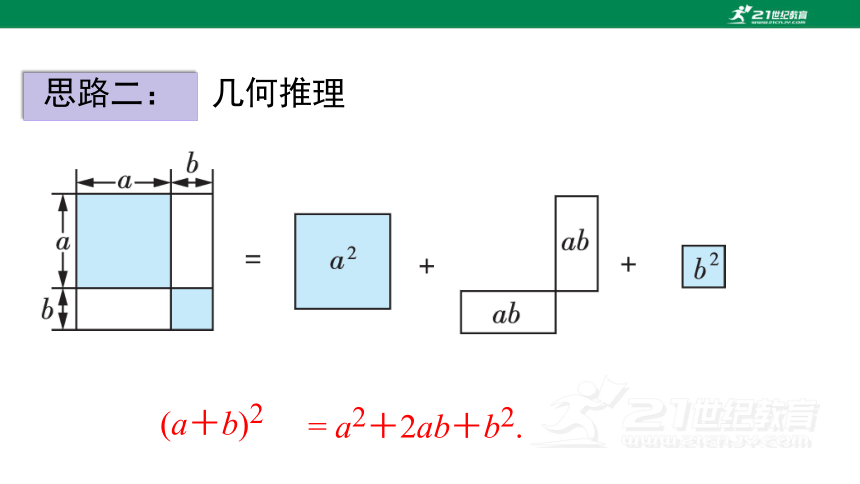
思路二:
(a+b)2
= a2+2ab+b2.
用两数和的完全平方公式计算(填空):
(a+1) 2 =____2 +2 . ___ . ___ + ___2 =_____________
(2) (2a+3b)2 =____2 +2 . ___ . ____+____2=____________
a
a
1
1
a2+2a+1
(2a)
3b
(3b)
2a
4a2+12ab+9b2
(a+b)2 =a2 +2ab+ b2
a与b可以是数、单项式或者更复杂的代数式
(3) ( p- 1 )2 = ( p - 1 )( p -1 ) = .
p2 - 2p + 1
(4) ( m-2 )2 = ( m-2 )( m-2 ) = .
m2-4m + 4
探究 2:
规律:两个数的差的平方,等于这两个数平方的和,减去它们的积的2 倍.
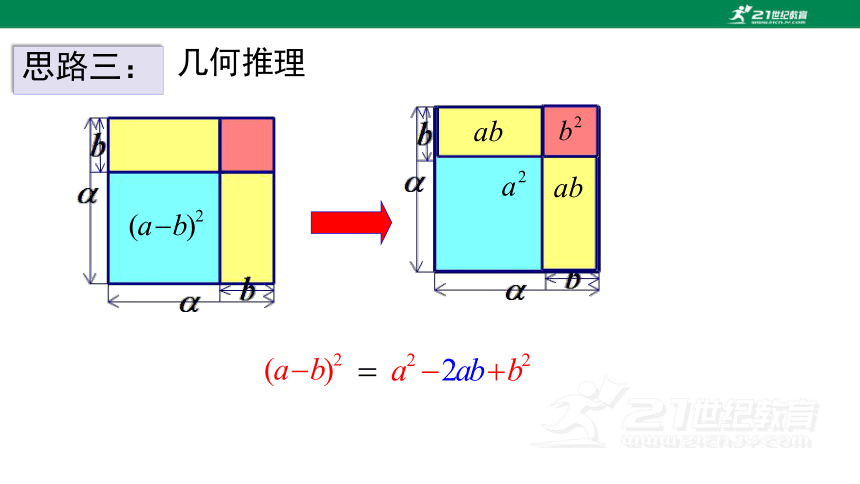
(a-b)2 = (a-b)(a-b)
= a2-2ab+b2.
= a2 - ab - ab + b2
思路一:
思路二:
(a-b)2
= [a+(-b)]2
= a2+2·a·(-b)+(-b)2
= a2-2ab+b2.
代数推理
运算要求:正确、灵活、合理、简洁
几何推理
思路三:
解: =
y2 - 2 · y · + ( )2
= y2 - y +
(a - b)2 = a2 - 2 · a · b + b2
计算: .
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a ± b)2 = a2 ± 2ab + b2
两个数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(口诀:“首平方,尾平方,积的2倍放中央”)
(首 ± 尾)2
= 首平方
+尾平方
± 积的2倍
例3 用完全平方公式计算:
⑴(x+2y)2. ⑵(2a-5)2. ⑶(-2s+t)2.
解⑴(x+2y)2=x2+4xy+4y2.
⑵(2a-5)2=4a2-20a+25.
解法二:(-2s+t)2=[(-2s)+t]2
⑶解法一:(-2s+t)2=(t-2s)2
=t2-2.t.(2s)+(2s)2
=t2-4st+4s2.
=(-2s)2+2.(-2s).t+t2
=t2-4st+4s2.
运算要求:正确、灵活、合理、简洁
(3) (2x+y)2 =4x2 +2xy +y2
下面各式的计算错在哪里?应当怎样改正?
应该为
应该为
(1);
(2)
应该为(2x+y)2 =4x2 +4xy +y2
用完全平方公式计算:⑷(-3x-4y)2.
⑷解法一:(-3x-4y)2=(-3x)2-2.(-3x).(4y)+(4y)2
=9x2+24xy+16y2.
解法二:(-3x-4y)2=(3x+4y)2
=9x2+24xy+16y2.
解法三:(-3x-4y)2=[(-3x)+(-4y)]2
=(-3x)2+2.(-3x).(-4y)+(-4y)2
=9x2+24xy+16y2.
通过上面计算大家发现: (a + b)2 (-a-b)2 、
=
运算要求:正确、灵活、合理、简洁
(1) 1022;
解:原式
= (100 + 2)2
= 10000 + 400 + 4
= 10404.
(2) 992.
解:原式
= (100 – 1)2
= 10000 - 200 + 1
= 9801.
运用完全平方公式计算:
例4:一花农有4块正方形茶花苗圃,边长分别为30.1m,29.5m,30m,27m。现将这4块苗圃的边长都增加1.5m,求各苗圃的面积分别增加了多少m ?
解:设原正方形苗圃边长为am,
∴新正方形的边长为(a+1.5)m,
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,
3a+2.25=3×30.1+2.25=92.55
当a=29.5时,
3a+2.25=3×29.5+2.25=90.75
类似地,当a=30, a=27时, 3a+2.25的值分别为92.25,83.25
答:苗圃面积分别增加了92.55m2,90.75m2 92.25m2,83.25m2.
a
a
1.5
1.5
将一块边长为a米的正方形广场进行扩建,扩建后的正方形边长比原来长2米,则扩建后广场面积增大了( )
A. 4平方米 B. 平方米
C. ()平方米 D. ()平方米
【解析】由题意可知,用扩大后的面积减去原来的面积即可得到增大的面积,所以扩建后广场面积增大了.
D
1.运用完全平方公式计算:
(1); (2);
(3); (4).
解:原式=.
解:原式=.
解:原式=+25.
解:原式=.
夯实基础,稳扎稳打
2. 计算:
(1)
(2)
.
(4)
=.
.
连续递推,豁然开朗
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4 乘法公式(2)
浙教版七年级下册
1.合并同类项:
温故知新:
-xy-xy= .
ab+ab= ;
2ab
-2xy
2.多项式乘多项式:
(a+b)(p+q)
=ap
+aq
+bp
+bq
多项式与多项式相乘的展开式
3.根据乘方的定义,我们知道:a2=a·a,
那么(a+b)2 可以写成:
(a+b)2=
(a+b)(a+b)
(1) ( p + 1 )2 = = .
探究 1:
(2) ( m + 2 )2 = = .
p2 + p + p + 12
m2 + 2m + 2m + 22
两数的___的平方
和
两数____的和,
平方
加上它们积的__倍
2
p2 + 2p + 1
m2 + 4m + 4
规律:两个数和的平方,等于这两个数的平方的和,
加上这两个数积的2倍.
∵(a+b)2 = (a+b)(a+b)
= a2+2ab+b2.
= a2 + ab + ab + b2
思路一:
代数推理
几何推理
思路二:
(a+b)2
= a2+2ab+b2.
用两数和的完全平方公式计算(填空):
(a+1) 2 =____2 +2 . ___ . ___ + ___2 =_____________
(2) (2a+3b)2 =____2 +2 . ___ . ____+____2=____________
a
a
1
1
a2+2a+1
(2a)
3b
(3b)
2a
4a2+12ab+9b2
(a+b)2 =a2 +2ab+ b2
a与b可以是数、单项式或者更复杂的代数式
(3) ( p- 1 )2 = ( p - 1 )( p -1 ) = .
p2 - 2p + 1
(4) ( m-2 )2 = ( m-2 )( m-2 ) = .
m2-4m + 4
探究 2:
规律:两个数的差的平方,等于这两个数平方的和,减去它们的积的2 倍.
(a-b)2 = (a-b)(a-b)
= a2-2ab+b2.
= a2 - ab - ab + b2
思路一:
思路二:
(a-b)2
= [a+(-b)]2
= a2+2·a·(-b)+(-b)2
= a2-2ab+b2.
代数推理
运算要求:正确、灵活、合理、简洁
几何推理
思路三:
解: =
y2 - 2 · y · + ( )2
= y2 - y +
(a - b)2 = a2 - 2 · a · b + b2
计算: .
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.
可以合写成 (a ± b)2 = a2 ± 2ab + b2
两个数和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.
(口诀:“首平方,尾平方,积的2倍放中央”)
(首 ± 尾)2
= 首平方
+尾平方
± 积的2倍
例3 用完全平方公式计算:
⑴(x+2y)2. ⑵(2a-5)2. ⑶(-2s+t)2.
解⑴(x+2y)2=x2+4xy+4y2.
⑵(2a-5)2=4a2-20a+25.
解法二:(-2s+t)2=[(-2s)+t]2
⑶解法一:(-2s+t)2=(t-2s)2
=t2-2.t.(2s)+(2s)2
=t2-4st+4s2.
=(-2s)2+2.(-2s).t+t2
=t2-4st+4s2.
运算要求:正确、灵活、合理、简洁
(3) (2x+y)2 =4x2 +2xy +y2
下面各式的计算错在哪里?应当怎样改正?
应该为
应该为
(1);
(2)
应该为(2x+y)2 =4x2 +4xy +y2
用完全平方公式计算:⑷(-3x-4y)2.
⑷解法一:(-3x-4y)2=(-3x)2-2.(-3x).(4y)+(4y)2
=9x2+24xy+16y2.
解法二:(-3x-4y)2=(3x+4y)2
=9x2+24xy+16y2.
解法三:(-3x-4y)2=[(-3x)+(-4y)]2
=(-3x)2+2.(-3x).(-4y)+(-4y)2
=9x2+24xy+16y2.
通过上面计算大家发现: (a + b)2 (-a-b)2 、
=
运算要求:正确、灵活、合理、简洁
(1) 1022;
解:原式
= (100 + 2)2
= 10000 + 400 + 4
= 10404.
(2) 992.
解:原式
= (100 – 1)2
= 10000 - 200 + 1
= 9801.
运用完全平方公式计算:
例4:一花农有4块正方形茶花苗圃,边长分别为30.1m,29.5m,30m,27m。现将这4块苗圃的边长都增加1.5m,求各苗圃的面积分别增加了多少m ?
解:设原正方形苗圃边长为am,
∴新正方形的边长为(a+1.5)m,
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,
3a+2.25=3×30.1+2.25=92.55
当a=29.5时,
3a+2.25=3×29.5+2.25=90.75
类似地,当a=30, a=27时, 3a+2.25的值分别为92.25,83.25
答:苗圃面积分别增加了92.55m2,90.75m2 92.25m2,83.25m2.
a
a
1.5
1.5
将一块边长为a米的正方形广场进行扩建,扩建后的正方形边长比原来长2米,则扩建后广场面积增大了( )
A. 4平方米 B. 平方米
C. ()平方米 D. ()平方米
【解析】由题意可知,用扩大后的面积减去原来的面积即可得到增大的面积,所以扩建后广场面积增大了.
D
1.运用完全平方公式计算:
(1); (2);
(3); (4).
解:原式=.
解:原式=.
解:原式=+25.
解:原式=.
夯实基础,稳扎稳打
2. 计算:
(1)
(2)
.
(4)
=.
.
连续递推,豁然开朗
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
