浙教版七年级下册培优训练: 逢拐点,作截线 (含答案)
文档属性
| 名称 | 浙教版七年级下册培优训练: 逢拐点,作截线 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 799.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-19 23:03:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
逢“拐点”,作截线
夯实基础,稳扎稳打
1.证明;三角形内角和等于1800
2..如图,已知∠AEC=∠A+∠C,试说明:AB∥CD.
3.如图,=360° 证明:,
( http: / / www.21cnjy.com / )
4.如图,AB∥CD,证明:∠BAP+∠P+∠DCP=360°.
5.如图,AB∥CD,P为AB,CD之间的一点.已知∠1=32°,∠2=25°,求∠BPD的度数.
连续递推,豁然开朗
6.如图,a∥b,∠1=105°,∠2=140°,求∠3的度数
7.如图,若直线,,,求的度数.
8.如图,AB∥EF,∠C=90°,求α、β和γ的关系
.
9.如图,已知AB∥CD,∠1=∠2,试说明:∠E=∠F.
思维拓展,更上一层
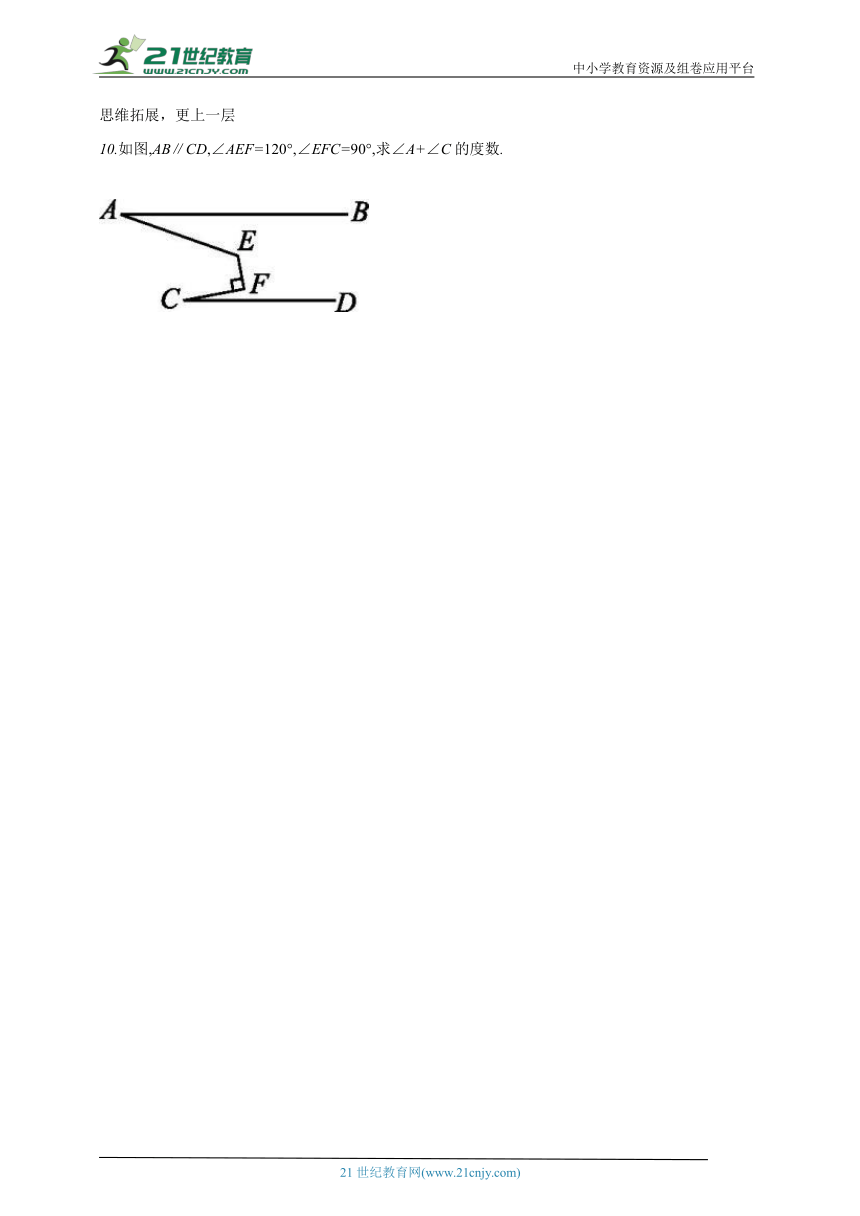
10.如图,AB∥CD,∠AEF=120°,∠EFC=90°,求∠A+∠C的度数.
11.如图,已知,P是直线,间的一点,于点F,PE交AB于点E,.
(1)求的度数;(2)如图2,射线从出发,以每秒的速度绕P点按逆时针方向旋转,当垂直时,立刻按原速返回至后停止运动;射线从出发,以每秒的速度绕E点按逆时针方向旋转至后停止运动.若射线,射线同时开始运动,设运动时间为t秒.
①当时,求的度数;②当时,求t的值.
逢“拐点”,作截线参考答案
1.过点A作PQ∥BC。∠1=∠B(两直线平行,内错角相等)∠2=∠C(两直线平行,内错角相等)。
又∵∠1+∠2+∠3=180°(平角的定义)。∴∠BAC+∠B+∠C=180°(等量代换)。
2.解:如图,延长CE交AB于点F.
∵∠AEC=∠A+∠C,∠AEC+∠AEF=180°,∴∠AEF+∠A+∠C=180°.
又∵∠AFE+∠A+∠AEF=180°,∴∠AFE=∠C,∴AB∥CD.
( http: / / www.21cnjy.com / )
3.解:连接AD,=360°,∠2+∠ACD+∠ADC=180°,
,∴∠BAD +∠ADE=180°,.
4.解:连接AC.∵AB∥CD,∴∠BAC+∠DCA=180°,
∵∠P+∠PAC+∠PCA=180°,∴∠BAP+∠P+∠DCP=∠BAC+∠DCA+∠P+∠PAC+∠PCA=360°.
5.解:如图,延长BP交CD于点F.∵AB∥CD,∴∠3=∠1=32°.
∵∠2=25°,∴∠FPD=180°-25°-32°=123°,∴∠BPD=180°-123°=57°.
6.解:如图作出两直线的交点,∵a∥b,则∠1+∠4=180°,∴∠4=75°,
根据三角形的外角等于不相邻的两个内角的和得到∠2=∠3+∠4,则∠3=65°.
7.如图所示,点在直线上,点、在直线上,点在、之间,为,
直线,,,,,
.
8.解:延长DC交AB与G,延长CD交EF于H.
在直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,
∵AB∥EF,∴∠1=∠2,∴90°﹣α=β﹣γ,即α+β﹣γ=90°.
9.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵AB∥CD,∴∠DHF=∠EGA.∵∠1=∠2,∴∠2+∠DHF=∠1+∠EGA.
∵∠2+∠DHF+∠DFH=180°,∠1+∠EGA+∠AEG=180°,∠DFH+∠DFE=180°,∠AEG+∠FEA=180°,
∴∠DFE=∠2+∠DHF,∠FEA=∠1+∠EGA,∴∠DFE=∠FEA.
10.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵∠AEF=120°,∠EFC=90°,∴∠AEG=60°,∠CFH=90°.
∵∠A+∠AEG+∠AGE=180°,∠C+∠CHF+∠CFH=180°,∠AGE+∠BGE=180°,∠CHF+∠FHD=180°,
∴∠A+∠AEG=∠BGE,∠C+∠CFH=∠FHD.
∵AB∥CD,∴∠BGE+∠FHD=180°,∴∠A+∠AEG+∠C+∠CFH=180°,
∴∠A+∠C=180°-∠AEG-∠CFH=180°-60°-90°=30°.
(11)解:延长与相交于点G,如图1,
∵,∴,
∵,∴;
(2)解:①Ⅰ如图2,
∵,,∴,
∴射线的运动时间,∴射线PN旋转的角度,
又∵,∴;
Ⅱ如图3所示,∵,,∴,
∴射线运动的时间,∴射线旋转的角度:
又∵,∴;∴的度数为或;
②Ⅰ当从出发,运动如图4时,,与相交于点H,
根据题意可知,经过t秒,,,
∵,∴,
又∵,∴,解得;
Ⅱ射线垂直后,再顺时针向运动时,运动如图5时,,
根据题意可知,,,,射线的转动度数为,
则,又∵,∴,∴,解得;
Ⅲ当从出发,运动如图6时,此时垂直后立刻按原速返回的过程中,,
根据题意可知,经过t秒,,,
∵,,∴,,
又∵,∴,∴,解得,
综上所述:满足条件的t的值为秒或秒或秒.
C
B
A
1
C
B
A
2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
逢“拐点”,作截线
夯实基础,稳扎稳打
1.证明;三角形内角和等于1800
2..如图,已知∠AEC=∠A+∠C,试说明:AB∥CD.
3.如图,=360° 证明:,
( http: / / www.21cnjy.com / )
4.如图,AB∥CD,证明:∠BAP+∠P+∠DCP=360°.
5.如图,AB∥CD,P为AB,CD之间的一点.已知∠1=32°,∠2=25°,求∠BPD的度数.
连续递推,豁然开朗
6.如图,a∥b,∠1=105°,∠2=140°,求∠3的度数
7.如图,若直线,,,求的度数.
8.如图,AB∥EF,∠C=90°,求α、β和γ的关系
.
9.如图,已知AB∥CD,∠1=∠2,试说明:∠E=∠F.
思维拓展,更上一层
10.如图,AB∥CD,∠AEF=120°,∠EFC=90°,求∠A+∠C的度数.
11.如图,已知,P是直线,间的一点,于点F,PE交AB于点E,.
(1)求的度数;(2)如图2,射线从出发,以每秒的速度绕P点按逆时针方向旋转,当垂直时,立刻按原速返回至后停止运动;射线从出发,以每秒的速度绕E点按逆时针方向旋转至后停止运动.若射线,射线同时开始运动,设运动时间为t秒.
①当时,求的度数;②当时,求t的值.
逢“拐点”,作截线参考答案
1.过点A作PQ∥BC。∠1=∠B(两直线平行,内错角相等)∠2=∠C(两直线平行,内错角相等)。
又∵∠1+∠2+∠3=180°(平角的定义)。∴∠BAC+∠B+∠C=180°(等量代换)。
2.解:如图,延长CE交AB于点F.
∵∠AEC=∠A+∠C,∠AEC+∠AEF=180°,∴∠AEF+∠A+∠C=180°.
又∵∠AFE+∠A+∠AEF=180°,∴∠AFE=∠C,∴AB∥CD.
( http: / / www.21cnjy.com / )
3.解:连接AD,=360°,∠2+∠ACD+∠ADC=180°,
,∴∠BAD +∠ADE=180°,.
4.解:连接AC.∵AB∥CD,∴∠BAC+∠DCA=180°,
∵∠P+∠PAC+∠PCA=180°,∴∠BAP+∠P+∠DCP=∠BAC+∠DCA+∠P+∠PAC+∠PCA=360°.
5.解:如图,延长BP交CD于点F.∵AB∥CD,∴∠3=∠1=32°.
∵∠2=25°,∴∠FPD=180°-25°-32°=123°,∴∠BPD=180°-123°=57°.
6.解:如图作出两直线的交点,∵a∥b,则∠1+∠4=180°,∴∠4=75°,
根据三角形的外角等于不相邻的两个内角的和得到∠2=∠3+∠4,则∠3=65°.
7.如图所示,点在直线上,点、在直线上,点在、之间,为,
直线,,,,,
.
8.解:延长DC交AB与G,延长CD交EF于H.
在直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,
∵AB∥EF,∴∠1=∠2,∴90°﹣α=β﹣γ,即α+β﹣γ=90°.
9.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵AB∥CD,∴∠DHF=∠EGA.∵∠1=∠2,∴∠2+∠DHF=∠1+∠EGA.
∵∠2+∠DHF+∠DFH=180°,∠1+∠EGA+∠AEG=180°,∠DFH+∠DFE=180°,∠AEG+∠FEA=180°,
∴∠DFE=∠2+∠DHF,∠FEA=∠1+∠EGA,∴∠DFE=∠FEA.
10.解:如图,延长EF交CD于点H,延长FE交AB于点G.
∵∠AEF=120°,∠EFC=90°,∴∠AEG=60°,∠CFH=90°.
∵∠A+∠AEG+∠AGE=180°,∠C+∠CHF+∠CFH=180°,∠AGE+∠BGE=180°,∠CHF+∠FHD=180°,
∴∠A+∠AEG=∠BGE,∠C+∠CFH=∠FHD.
∵AB∥CD,∴∠BGE+∠FHD=180°,∴∠A+∠AEG+∠C+∠CFH=180°,
∴∠A+∠C=180°-∠AEG-∠CFH=180°-60°-90°=30°.
(11)解:延长与相交于点G,如图1,
∵,∴,
∵,∴;
(2)解:①Ⅰ如图2,
∵,,∴,
∴射线的运动时间,∴射线PN旋转的角度,
又∵,∴;
Ⅱ如图3所示,∵,,∴,
∴射线运动的时间,∴射线旋转的角度:
又∵,∴;∴的度数为或;
②Ⅰ当从出发,运动如图4时,,与相交于点H,
根据题意可知,经过t秒,,,
∵,∴,
又∵,∴,解得;
Ⅱ射线垂直后,再顺时针向运动时,运动如图5时,,
根据题意可知,,,,射线的转动度数为,
则,又∵,∴,∴,解得;
Ⅲ当从出发,运动如图6时,此时垂直后立刻按原速返回的过程中,,
根据题意可知,经过t秒,,,
∵,,∴,,
又∵,∴,∴,解得,
综上所述:满足条件的t的值为秒或秒或秒.
C
B
A
1
C
B
A
2
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
