浙教版七年级下册第一章《相交线与平行线》提升练: 想,一判二推三要使;写,条分缕析,有序表达(含答案)
文档属性
| 名称 | 浙教版七年级下册第一章《相交线与平行线》提升练: 想,一判二推三要使;写,条分缕析,有序表达(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 11:42:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
想,一判二推三要使;写,条分缕析,有序表达---言而有据,合乎逻辑;表达规范,推理严谨(1)
夯实基础,稳扎稳打
1.如图,,.求证:.
证明:∵(已知),∴ ( ).
∴ ( ).
∵( 已知 ),∴ (等量代换).
∴(同旁内角互补,两直线平行).
2.如图,点G在上,已知,平分,平分,求证
解:(已知),( )
( ).
∵平分,_______( ).
平分,_______,得( ),
( ).
3.如图,已知,,于点D,于点,求证:
解:∵,,,
( )( )
又,(已知),( ),
( ),(等量代换).
4.如图,,,.(1)求证:;(2)求证://
解:(1)∵(已知) ________( )
又(已知)________( )
( )
(2)∵(已知)∴________( )
又∵(已知)∴________________(等量代换)∴________
连续递推,豁然开朗
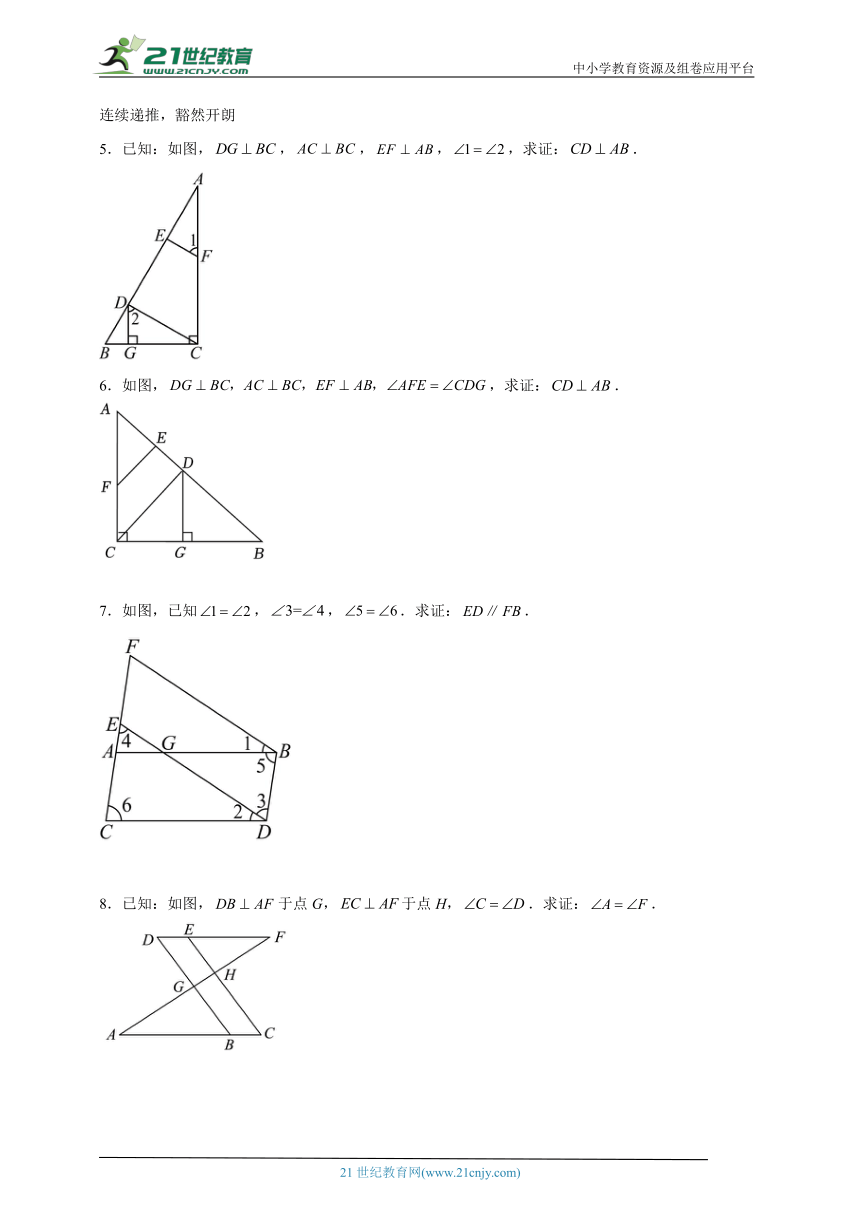
5.已知:如图,,,,,求证:.
6.如图,,求证:.
7.如图,已知,,.求证:.
8.已知:如图,于点G,于点H,.求证:.
思维拓展,更上一层
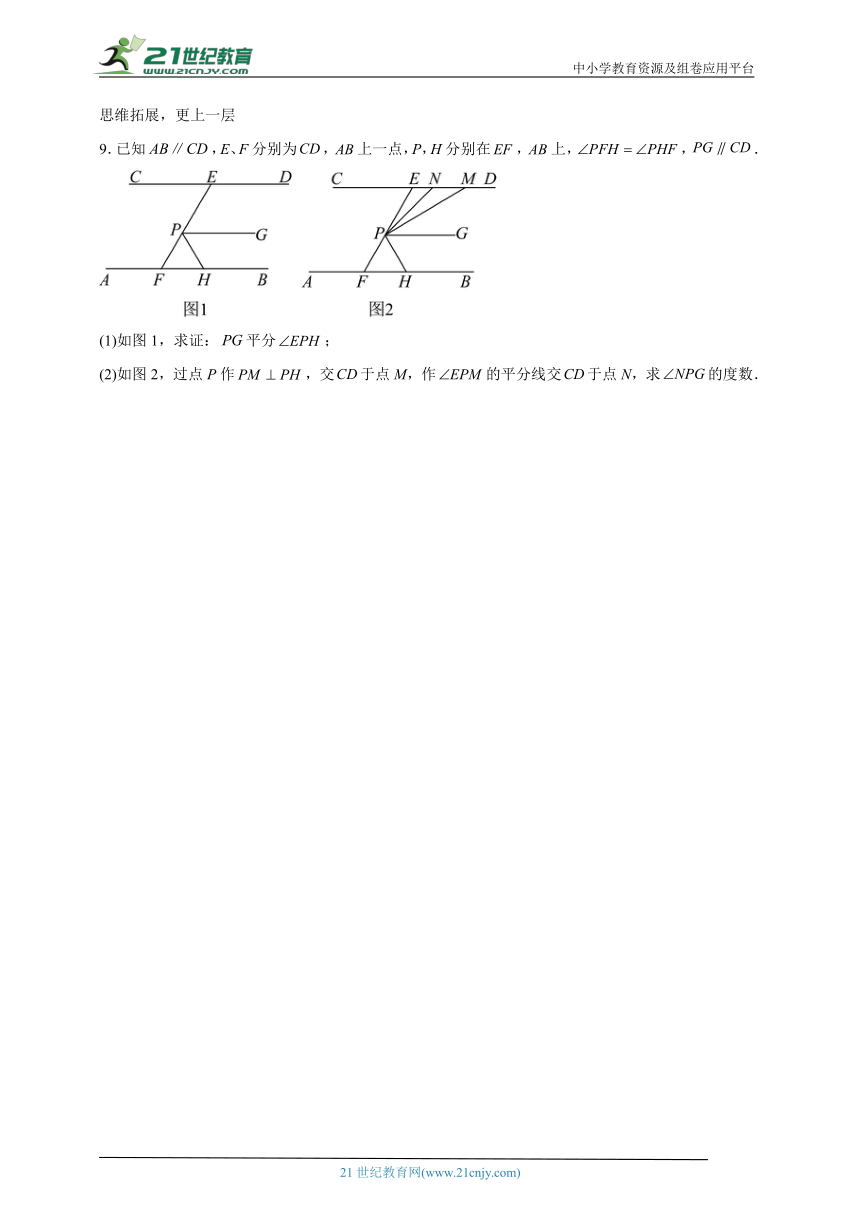
9.已知,E、F分别为,上一点,P,H分别在,上,,.
(1)如图1,求证:平分;
(2)如图2,过点P作,交于点M,作的平分线交于点N,求的度数.
10.如图,平分,.
(1)如图1,求证:;
(2)如图2,点F为线段上一点,连接,求证:;
(3)如图3,在(2)的条件下,在射线上取点G,连接,使得,当,时,求的度数;
想,一判二推三要使;写,条分缕析,有序表达---言而有据,合乎逻辑;表达规范,推理严谨(1)
1.【答案】:;内错角相等,两直线平行;;两直线平行,同旁内角互补;.
2.【答案】邻补角的定义;同角的补角相等;;角平分线的定义;;等量代换;内错角相等,两直线平行;
3.【答案】①;②同旁内角互补,两直线平行;③两直线平行,内错角相等;④同一平面内,垂直于同一条直线的两条直线互相平行;⑤两直线平行,同位角相等.
4.【答案】(1);两直线平行,内错角相等;;等量代换;同位角相等,两直线平行;(2);两直线平行,内错角相等;;3 ;
5.【详解】证明:,(已知)
(垂直定义)(同位角相等,两直线平行)
(两直线平行,内错角相等)
(已知)(等量代换)(同位角相等,两直线平行)
(两直线平行,同位角相等)(已知)
(等量代换)
6.【详解】证明:∵,
∴(垂直的定义).∴(同位角相等,两直线平行).
∴(两直线平行,内错角相等).
∵,∴(等量代换).
∴(同位角相等,两直线平行).∴(两直线平行,同位角相等).
∵,∴.∴(等量代换).∴.
7.【详解】解:(已知),
(内错角相等,两直线平行),(两直线平行,同旁内角互补).
(已知),(等量代换),
(同旁内角互补,两直线平行),(两直线平行,同位角相等).
(已知),(等量代换),(同位角相等,两直线平行).
8.【详解】∵于点G,于点H (已知),∴(垂直的定义).
∴(同位角相等,两直线平行).∴(两直线平行,同位角相等).
∵(已知),∴(等量代换).
∴(内错角相等,两直线平行).∴(两直线平行,内错角相等).
9.【详解】(1)证明:∵,∴,
∴,,
∵,∴∴平分.
(2)设,∵平分,∴,
∵,∴,
∴,
∵平分,∴,∴.
10【详解】(1)证明:平分,,
,,;
(2)证明:过作,如图,
,,,,
,即;
(3)解:设,,,,
由(1)知:,,,
平分,,
,,,
,解得:,即.
想,一判二推三要使;写,条分缕析,有序表达----言而有据,合乎逻辑;表达规范,推理严谨(2)
夯实基础,稳扎稳打
1.如图,点在上,点在上,,,请说明.
证明:(已知) ∴( )
( )
AB//____( ) (两直线平行,同旁内角互补)
又(已知)(等量代换)
____ ( )( )
2.已知,如图,于H,求证:.
证明:∵( )∴ .
∵(已知),∴( );
∴ ( )∵(已知)
∴ ( )∴ (内错角相等,两直线平行)
= (两直线平行,同位角相等),∴
3.如图,已知于点D,于点F,求证:=
解:(已知),,
( )( )
(已知),
( ),
( ),( )
4.如图,已知,,点,分别在线段,上,求证:.
解:∵(已知),( ),∴( ),
∴________( ),∴________(两直线平行,同位角相等).
又∵(已知),∴________(等量代换),
∴________( ),∴( ).
连续递推,豁然开朗
5.如图,四边形,,于点,于点,求证:.
6.已知:如图,求证:
7..如图:已知,,于点,于点,求证:.
8..如图,四边形中,F为上一点,连接并延长,交的延长线于点E,连接.若,,.(1)试说明;(2)与的位置关系如何?为什么?
(3)与相等吗?请说明理由.
思维拓展,更上一层
9.如图,在△ABC中,于点D,点E在上,于点F,过点D作直线交于点G,交的延长线于点H,,.求的度数.
10 .问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷,如图(1)是一个“互”字,如图(2)是由图(1)抽象的几何图形,其中,.点,,在同一直线上,点,,在同一直线上,且.(1)求证://(2)求证:
想,一判二推三要使;写,条分缕析,有序表达-----言而有据,合乎逻辑;表达规范,推理严谨(2)
1.【答案】对顶角相等;等量代换;;同位角相等,两直线平行;;;同旁内角互补,两直线平行;两直线平行,内错角相等
2.【答案】已知;;同位角相等,两直线平行;;两直线平行,内错角相等;;等量代换;;;
3.【答案】同旁内角互补,两直线平行;两直线平行,内错角相等;同一平面内,垂直于同一条直线的两条直线平行;;两直线平行,同位角相等;等量代换
4.【答案】对顶角相等;等量代换;;同位角相等,两直线平行;;;;内错角相等,两直线平行;两直线平行,内错角相等
5.【详解】解:,理由如下:(已知),
(同旁内角互补,两直线平行),(两直线平行,内错角相等),
,(已知),(垂直于同一条直线的两条直线平行),
(两直线平行,同位角相等),(等量代换).
6.【详解】证明(已知),
(内错角相等,两直线平行)(两直线平行,内错角相等)
(已知),(等量代换),
(内错角相等,两直线平行)(两直线平行,同位角相等)
7.【详解】证明:∵,(已知),∴,
∴(同旁内角互补,两直线平行),∴(两直线平行,内错角相等)
∵,(已知),∴,(垂直的定义)
∴,∴(同位角相等,两直线平行),
∴(两直线平行,同位角相等),∴(等量代换).
8.【详解】(1)解:∵,(已知)∴.(同位角相等,两直线平行)
(2)解:与的位置关系是:,理由如下:
∵,(已知)∴.(两直线平行,同位角相等)
∵,(已知)∴.(等量代换)
∵,(已知)∴.即,
∴,(等量代换)∴.(内错角相等,两直线平行)
(3)解:,理由如下:
∵,∴.∵,∴.∵,∴.
9.【详解】解:,(已知)
.(垂直于同一直线的两直线平行)
.(两直线平行、同旁内角互补)
,(已知)
.(同角的补角相等)
.(内错角相等,两直线平行)
.(两直线平行,内错角相等)
,(已知)
.(等量代换)
,(已知)
.(垂直的定义)
,(平角定义)
.(等式性质)
(已证),
.(两直线平行,同位角相等).
10【解析】(1),,
,;
(2)延长交于点,,,
,,,
,,
脑中金箍棒一闪,一顿噼里啪啦--------推理给我带来快乐
1.如图,已知点E、F在直线上,点N在线段上,与交于点M,,.
(1)求证:;(2)若,,求的度数.
2.如图,交于点F,点C在的延长线上,.
(1)若,求的度数.(2)若,求证:
.
3.如图,,与交于点P.
(1)若,求的度数;
(2)若,,求证:.
4.如图,点C,D在直线上,,.
(1)求证:;(2)的角平分线交于点G,若,求的度数.
5.如图,,,的平分线交的延长线于点.
(1)求证:;(2)探究,,之间的数量关系,并说明理由;
6.如图,已知,平分,交于点.(1)求证:;
(2)若于点,,求的度数.
7.如图,已知,.(1)求证:;
(2)若,的角平分线与的角平分线交于点F,与交于点M,,求的度数.
8.如图,已知,,点E在线段延长线上,平分.
(1)求证:;(2)若,,求的度数.
脑中金箍棒一闪,一顿噼里啪啦--------推理给我带来快乐
1.【详解】(1)证明:,,,
又,,.
(2)解:,,,,
,,
,.
2.【详解】(1)解:,
,.,,即.
(2)证明:由(1),可知,.又,,
3.【详解】(1)解:∵,∴,∴,∵,∴.
(2)证明:∵,∴,∵,∴,∴,
由(1)可知,,∴,∴.
4.【详解】(1),且,,;
(2),,,
又为的角平分线,,
,(方法不唯一).
5.【详解】(1)证明:∵,∴,
∵,,∴,∴;
(2)解:,如图,作,
则,由()可得,∴,∴,
∴,∵,∴.
6【详解】(1)证明:平分,,,,;
(2)解:,,
,,
,,,
平分,,,.
7.【详解】(1)解:如图:
∵∴∵∴∴;
(2)解:如图:过点F作直线,
∵,∴,∴,
∵平分,∴,
∵,,∴,
∵,∴,
∵平分,∴,
∵,∴,∴.
8【详解】(1)证明:∵,∴,
∵ ,∴ ,∴;
∴ ,∵平分,∴,∴ ;
(2)解:∵,,
可设,∴,
∵,∴,
∵平分,∴∴
∵,
∴,即∴,
解得:,∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
想,一判二推三要使;写,条分缕析,有序表达---言而有据,合乎逻辑;表达规范,推理严谨(1)
夯实基础,稳扎稳打
1.如图,,.求证:.
证明:∵(已知),∴ ( ).
∴ ( ).
∵( 已知 ),∴ (等量代换).
∴(同旁内角互补,两直线平行).
2.如图,点G在上,已知,平分,平分,求证
解:(已知),( )
( ).
∵平分,_______( ).
平分,_______,得( ),
( ).
3.如图,已知,,于点D,于点,求证:
解:∵,,,
( )( )
又,(已知),( ),
( ),(等量代换).
4.如图,,,.(1)求证:;(2)求证://
解:(1)∵(已知) ________( )
又(已知)________( )
( )
(2)∵(已知)∴________( )
又∵(已知)∴________________(等量代换)∴________
连续递推,豁然开朗
5.已知:如图,,,,,求证:.
6.如图,,求证:.
7.如图,已知,,.求证:.
8.已知:如图,于点G,于点H,.求证:.
思维拓展,更上一层
9.已知,E、F分别为,上一点,P,H分别在,上,,.
(1)如图1,求证:平分;
(2)如图2,过点P作,交于点M,作的平分线交于点N,求的度数.
10.如图,平分,.
(1)如图1,求证:;
(2)如图2,点F为线段上一点,连接,求证:;
(3)如图3,在(2)的条件下,在射线上取点G,连接,使得,当,时,求的度数;
想,一判二推三要使;写,条分缕析,有序表达---言而有据,合乎逻辑;表达规范,推理严谨(1)
1.【答案】:;内错角相等,两直线平行;;两直线平行,同旁内角互补;.
2.【答案】邻补角的定义;同角的补角相等;;角平分线的定义;;等量代换;内错角相等,两直线平行;
3.【答案】①;②同旁内角互补,两直线平行;③两直线平行,内错角相等;④同一平面内,垂直于同一条直线的两条直线互相平行;⑤两直线平行,同位角相等.
4.【答案】(1);两直线平行,内错角相等;;等量代换;同位角相等,两直线平行;(2);两直线平行,内错角相等;;3 ;
5.【详解】证明:,(已知)
(垂直定义)(同位角相等,两直线平行)
(两直线平行,内错角相等)
(已知)(等量代换)(同位角相等,两直线平行)
(两直线平行,同位角相等)(已知)
(等量代换)
6.【详解】证明:∵,
∴(垂直的定义).∴(同位角相等,两直线平行).
∴(两直线平行,内错角相等).
∵,∴(等量代换).
∴(同位角相等,两直线平行).∴(两直线平行,同位角相等).
∵,∴.∴(等量代换).∴.
7.【详解】解:(已知),
(内错角相等,两直线平行),(两直线平行,同旁内角互补).
(已知),(等量代换),
(同旁内角互补,两直线平行),(两直线平行,同位角相等).
(已知),(等量代换),(同位角相等,两直线平行).
8.【详解】∵于点G,于点H (已知),∴(垂直的定义).
∴(同位角相等,两直线平行).∴(两直线平行,同位角相等).
∵(已知),∴(等量代换).
∴(内错角相等,两直线平行).∴(两直线平行,内错角相等).
9.【详解】(1)证明:∵,∴,
∴,,
∵,∴∴平分.
(2)设,∵平分,∴,
∵,∴,
∴,
∵平分,∴,∴.
10【详解】(1)证明:平分,,
,,;
(2)证明:过作,如图,
,,,,
,即;
(3)解:设,,,,
由(1)知:,,,
平分,,
,,,
,解得:,即.
想,一判二推三要使;写,条分缕析,有序表达----言而有据,合乎逻辑;表达规范,推理严谨(2)
夯实基础,稳扎稳打
1.如图,点在上,点在上,,,请说明.
证明:(已知) ∴( )
( )
AB//____( ) (两直线平行,同旁内角互补)
又(已知)(等量代换)
____ ( )( )
2.已知,如图,于H,求证:.
证明:∵( )∴ .
∵(已知),∴( );
∴ ( )∵(已知)
∴ ( )∴ (内错角相等,两直线平行)
= (两直线平行,同位角相等),∴
3.如图,已知于点D,于点F,求证:=
解:(已知),,
( )( )
(已知),
( ),
( ),( )
4.如图,已知,,点,分别在线段,上,求证:.
解:∵(已知),( ),∴( ),
∴________( ),∴________(两直线平行,同位角相等).
又∵(已知),∴________(等量代换),
∴________( ),∴( ).
连续递推,豁然开朗
5.如图,四边形,,于点,于点,求证:.
6.已知:如图,求证:
7..如图:已知,,于点,于点,求证:.
8..如图,四边形中,F为上一点,连接并延长,交的延长线于点E,连接.若,,.(1)试说明;(2)与的位置关系如何?为什么?
(3)与相等吗?请说明理由.
思维拓展,更上一层
9.如图,在△ABC中,于点D,点E在上,于点F,过点D作直线交于点G,交的延长线于点H,,.求的度数.
10 .问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷,如图(1)是一个“互”字,如图(2)是由图(1)抽象的几何图形,其中,.点,,在同一直线上,点,,在同一直线上,且.(1)求证://(2)求证:
想,一判二推三要使;写,条分缕析,有序表达-----言而有据,合乎逻辑;表达规范,推理严谨(2)
1.【答案】对顶角相等;等量代换;;同位角相等,两直线平行;;;同旁内角互补,两直线平行;两直线平行,内错角相等
2.【答案】已知;;同位角相等,两直线平行;;两直线平行,内错角相等;;等量代换;;;
3.【答案】同旁内角互补,两直线平行;两直线平行,内错角相等;同一平面内,垂直于同一条直线的两条直线平行;;两直线平行,同位角相等;等量代换
4.【答案】对顶角相等;等量代换;;同位角相等,两直线平行;;;;内错角相等,两直线平行;两直线平行,内错角相等
5.【详解】解:,理由如下:(已知),
(同旁内角互补,两直线平行),(两直线平行,内错角相等),
,(已知),(垂直于同一条直线的两条直线平行),
(两直线平行,同位角相等),(等量代换).
6.【详解】证明(已知),
(内错角相等,两直线平行)(两直线平行,内错角相等)
(已知),(等量代换),
(内错角相等,两直线平行)(两直线平行,同位角相等)
7.【详解】证明:∵,(已知),∴,
∴(同旁内角互补,两直线平行),∴(两直线平行,内错角相等)
∵,(已知),∴,(垂直的定义)
∴,∴(同位角相等,两直线平行),
∴(两直线平行,同位角相等),∴(等量代换).
8.【详解】(1)解:∵,(已知)∴.(同位角相等,两直线平行)
(2)解:与的位置关系是:,理由如下:
∵,(已知)∴.(两直线平行,同位角相等)
∵,(已知)∴.(等量代换)
∵,(已知)∴.即,
∴,(等量代换)∴.(内错角相等,两直线平行)
(3)解:,理由如下:
∵,∴.∵,∴.∵,∴.
9.【详解】解:,(已知)
.(垂直于同一直线的两直线平行)
.(两直线平行、同旁内角互补)
,(已知)
.(同角的补角相等)
.(内错角相等,两直线平行)
.(两直线平行,内错角相等)
,(已知)
.(等量代换)
,(已知)
.(垂直的定义)
,(平角定义)
.(等式性质)
(已证),
.(两直线平行,同位角相等).
10【解析】(1),,
,;
(2)延长交于点,,,
,,,
,,
脑中金箍棒一闪,一顿噼里啪啦--------推理给我带来快乐
1.如图,已知点E、F在直线上,点N在线段上,与交于点M,,.
(1)求证:;(2)若,,求的度数.
2.如图,交于点F,点C在的延长线上,.
(1)若,求的度数.(2)若,求证:
.
3.如图,,与交于点P.
(1)若,求的度数;
(2)若,,求证:.
4.如图,点C,D在直线上,,.
(1)求证:;(2)的角平分线交于点G,若,求的度数.
5.如图,,,的平分线交的延长线于点.
(1)求证:;(2)探究,,之间的数量关系,并说明理由;
6.如图,已知,平分,交于点.(1)求证:;
(2)若于点,,求的度数.
7.如图,已知,.(1)求证:;
(2)若,的角平分线与的角平分线交于点F,与交于点M,,求的度数.
8.如图,已知,,点E在线段延长线上,平分.
(1)求证:;(2)若,,求的度数.
脑中金箍棒一闪,一顿噼里啪啦--------推理给我带来快乐
1.【详解】(1)证明:,,,
又,,.
(2)解:,,,,
,,
,.
2.【详解】(1)解:,
,.,,即.
(2)证明:由(1),可知,.又,,
3.【详解】(1)解:∵,∴,∴,∵,∴.
(2)证明:∵,∴,∵,∴,∴,
由(1)可知,,∴,∴.
4.【详解】(1),且,,;
(2),,,
又为的角平分线,,
,(方法不唯一).
5.【详解】(1)证明:∵,∴,
∵,,∴,∴;
(2)解:,如图,作,
则,由()可得,∴,∴,
∴,∵,∴.
6【详解】(1)证明:平分,,,,;
(2)解:,,
,,
,,,
平分,,,.
7.【详解】(1)解:如图:
∵∴∵∴∴;
(2)解:如图:过点F作直线,
∵,∴,∴,
∵平分,∴,
∵,,∴,
∵,∴,
∵平分,∴,
∵,∴,∴.
8【详解】(1)证明:∵,∴,
∵ ,∴ ,∴;
∴ ,∵平分,∴,∴ ;
(2)解:∵,,
可设,∴,
∵,∴,
∵平分,∴∴
∵,
∴,即∴,
解得:,∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
