浙教版七下第一章专项训练:描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(含答案)
文档属性
| 名称 | 浙教版七下第一章专项训练:描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-01 21:30:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(1)
夯实基础,稳扎稳打
1.如图,,,相交于点,证明://
2.已知:如图,,.求证:.
3.如图,平分,平分,且,试说明:.
4.如图,已知,平分,,求证:.
5.已知,如图,直线,被直线所截,为与的交点,于点,,.试说明:.
连续递推,豁然开朗
6.如图, ,, .求证:.
7.如图,已知,,试说明:.
8.如图,直线、交于点,,分别平分和,已知,
求证:.
9.已知:如图,,,求证:.
10.如图所示,于点F,于点M,,.求证:.
思维拓展,更上一层
11.已知:如图,,求证:.
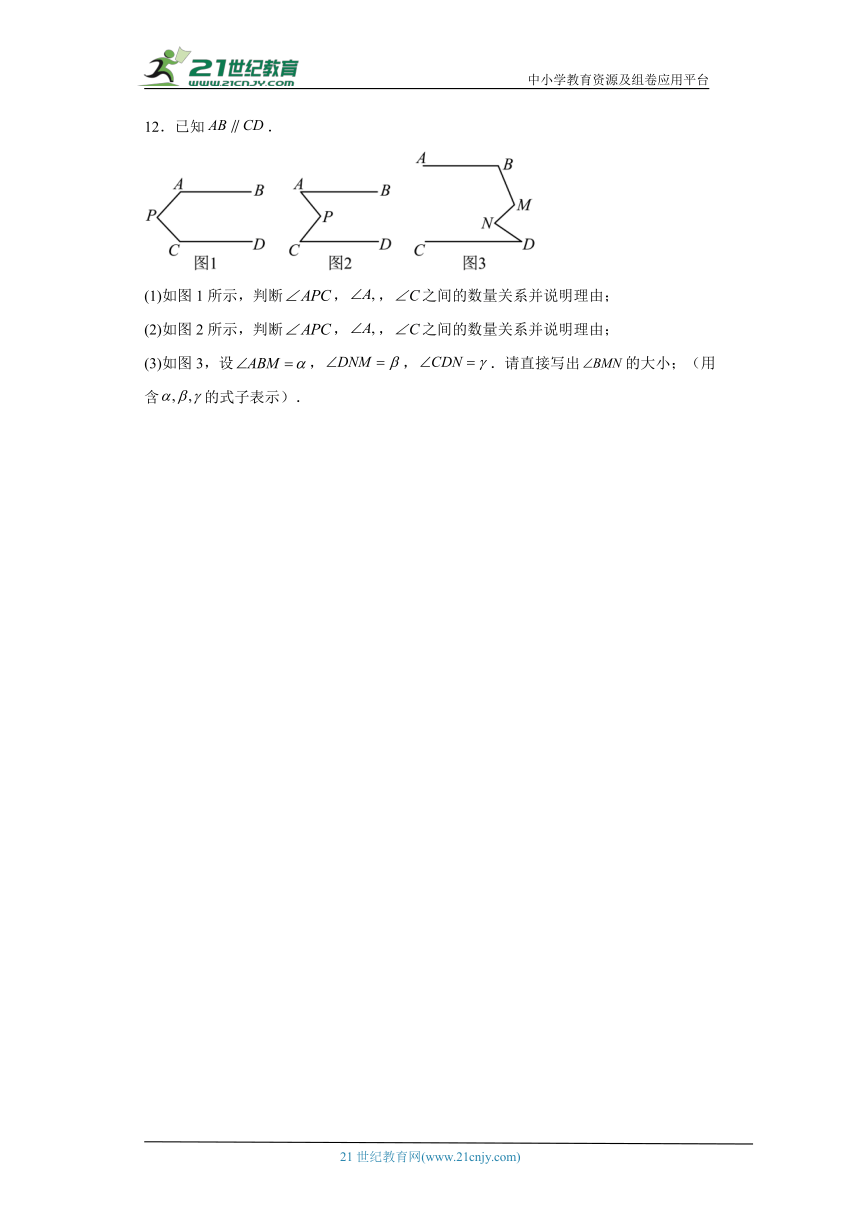
12.已知.
(1)如图1所示,判断,,之间的数量关系并说明理由;
(2)如图2所示,判断,,之间的数量关系并说明理由;
(3)如图3,设,,.请直接写出的大小;(用含的式子表示).
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(1)参考答案
1.解:因为,所以,因为,所以,.
2.证明:∵(已知),∴(两直线平行,内错角相等).
∵∴(等量代换)∴(同位角相等,两直线平行)
3.解:因为平分,所以.
因为平分,所以,
所以.
又因为,所以,,所以.
4.证明:∵平分,∴,
,∴,∴,∴
5.解:∵,∴.
∵,∴,∴.
∵,∴,∴.
6.证明:∵,,∴,
∴,∴,
∵,∴,∴.
7.解:因为,,所以,
所以,所以.因为,
所以,所以
8.证明:由(1)知,.
,,.
9. 证明:∵,∴,
∴,即,又∵,∴,
∴,∴.
10.证明:∵,(已知)∴(垂直定义)
∴(同位角相等,两直线平行)∴(两直线平行,同位角相等)
∵∴(等量代换)∴(内错角相等,两直线平行)
∵(已知)∴(内错角相等,两直线平行)
∴(平行于同一直线的两直线互相平行).
11.证明:∵(邻补角定义),
又∵(已知),∴(同角的补角相等),
∴(内错角相等,两直线平行),∴.
∵(已知),∴,(等量代换)
∴(同位角相等,两直线平行),∴(两直线平行,同位角相等),
12.(1),理由如下:
如图,作,,
,,,
即,
(2)理由如下:
如图,过点P作,
,,
,,,
(3)如图,过点M作,过点N作,
,,,,,
,,,,,,
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(2)
夯实基础,稳扎稳打
1.如图,直线、被所截,于H,,,求证:.
2.如图,已知直线,被直线所截,且.求证:;
3.如图所示,,,求证:.
4.如图,若,,求证:.
如图,直线分别与直线,交于点,,,且平分,平分.
求证:;
连续递推,豁然开朗
如图,,点E是直线上的一点,平分,,.
(1)求的度数;(2)若,求证:.
7.如图,E是四边形的边上一点,连接,已知,.求证:.
8.已知:如图,,和相交于点O,E是上一点,F是上一点,且.
(1)求证:;(2)若,求的度数.
9.如图,已知:,试判断与的关系,并说明理由.
如图,,,,.
(1)求证:;(2)求的度数.
思维拓展,更上一层
11.如图,已知,,且平分.求证:(1)
(2)平分
12.如图,已知.
(1)感知与探究:
如图1,已知请求出的度数;
(2)问题迁移:
如图2,、分别是的角平分线,的反向延长线与相交于点F,猜想与之间的数量关系,并说明理由;
(3)联想拓展:
在(2)的条件下,若,则的度数是_____________.
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(2)参考答案
1.证明:∵,∴∴∴
∵∴∴.
2证明:∵又∵,∴,∴.
3.证明:∵,∴.即
∵,∴,∴,
4.证明:∵,∴,
又∵,∴,∴.
5.(1)证明:平分,平分,,,
,,,.
6.(1)解:∵,,∴.
∵平分,∴;
(2)证明:∵,∴.
又∵,∴.
∵,∴,∵,∴,
∵,∴,∴,∴.
7证明:∵∴∵∴∴∴
∵∴∴∴
8.(1)解:,,,,;
(2)如图,过点作,,,,
,.
9.,解:,理由如下:,,
, , ,
∵,,, .
10(1)证明:∵∴,∵,∴,∴;
(2)∵∴,
∵, ∴,∴,
∵,∴.
11.(1)证明:,,
,,,,,;
(2)证明:平分,,,,,
,,平分.
12【详解】(1)如图,过点C作,
则,∴,
∴,∴
.
(2).理由如下:如图,过点F作,过点C作,
则,∴,
∵平分,平分,∴,,
∴ ,∴,
∵,∴,
∴,∴,
由①②可得,即.(3)由(2)知,,∵,
∴.
故答案为:.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(1)
夯实基础,稳扎稳打
1.如图,,,相交于点,证明://
2.已知:如图,,.求证:.
3.如图,平分,平分,且,试说明:.
4.如图,已知,平分,,求证:.
5.已知,如图,直线,被直线所截,为与的交点,于点,,.试说明:.
连续递推,豁然开朗
6.如图, ,, .求证:.
7.如图,已知,,试说明:.
8.如图,直线、交于点,,分别平分和,已知,
求证:.
9.已知:如图,,,求证:.
10.如图所示,于点F,于点M,,.求证:.
思维拓展,更上一层
11.已知:如图,,求证:.
12.已知.
(1)如图1所示,判断,,之间的数量关系并说明理由;
(2)如图2所示,判断,,之间的数量关系并说明理由;
(3)如图3,设,,.请直接写出的大小;(用含的式子表示).
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(1)参考答案
1.解:因为,所以,因为,所以,.
2.证明:∵(已知),∴(两直线平行,内错角相等).
∵∴(等量代换)∴(同位角相等,两直线平行)
3.解:因为平分,所以.
因为平分,所以,
所以.
又因为,所以,,所以.
4.证明:∵平分,∴,
,∴,∴,∴
5.解:∵,∴.
∵,∴,∴.
∵,∴,∴.
6.证明:∵,,∴,
∴,∴,
∵,∴,∴.
7.解:因为,,所以,
所以,所以.因为,
所以,所以
8.证明:由(1)知,.
,,.
9. 证明:∵,∴,
∴,即,又∵,∴,
∴,∴.
10.证明:∵,(已知)∴(垂直定义)
∴(同位角相等,两直线平行)∴(两直线平行,同位角相等)
∵∴(等量代换)∴(内错角相等,两直线平行)
∵(已知)∴(内错角相等,两直线平行)
∴(平行于同一直线的两直线互相平行).
11.证明:∵(邻补角定义),
又∵(已知),∴(同角的补角相等),
∴(内错角相等,两直线平行),∴.
∵(已知),∴,(等量代换)
∴(同位角相等,两直线平行),∴(两直线平行,同位角相等),
12.(1),理由如下:
如图,作,,
,,,
即,
(2)理由如下:
如图,过点P作,
,,
,,,
(3)如图,过点M作,过点N作,
,,,,,
,,,,,,
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(2)
夯实基础,稳扎稳打
1.如图,直线、被所截,于H,,,求证:.
2.如图,已知直线,被直线所截,且.求证:;
3.如图所示,,,求证:.
4.如图,若,,求证:.
如图,直线分别与直线,交于点,,,且平分,平分.
求证:;
连续递推,豁然开朗
如图,,点E是直线上的一点,平分,,.
(1)求的度数;(2)若,求证:.
7.如图,E是四边形的边上一点,连接,已知,.求证:.
8.已知:如图,,和相交于点O,E是上一点,F是上一点,且.
(1)求证:;(2)若,求的度数.
9.如图,已知:,试判断与的关系,并说明理由.
如图,,,,.
(1)求证:;(2)求的度数.
思维拓展,更上一层
11.如图,已知,,且平分.求证:(1)
(2)平分
12.如图,已知.
(1)感知与探究:
如图1,已知请求出的度数;
(2)问题迁移:
如图2,、分别是的角平分线,的反向延长线与相交于点F,猜想与之间的数量关系,并说明理由;
(3)联想拓展:
在(2)的条件下,若,则的度数是_____________.
描出与平行线相关的F、Z、U,锁定同位角、内错角、同旁内角(2)参考答案
1.证明:∵,∴∴∴
∵∴∴.
2证明:∵又∵,∴,∴.
3.证明:∵,∴.即
∵,∴,∴,
4.证明:∵,∴,
又∵,∴,∴.
5.(1)证明:平分,平分,,,
,,,.
6.(1)解:∵,,∴.
∵平分,∴;
(2)证明:∵,∴.
又∵,∴.
∵,∴,∵,∴,
∵,∴,∴,∴.
7证明:∵∴∵∴∴∴
∵∴∴∴
8.(1)解:,,,,;
(2)如图,过点作,,,,
,.
9.,解:,理由如下:,,
, , ,
∵,,, .
10(1)证明:∵∴,∵,∴,∴;
(2)∵∴,
∵, ∴,∴,
∵,∴.
11.(1)证明:,,
,,,,,;
(2)证明:平分,,,,,
,,平分.
12【详解】(1)如图,过点C作,
则,∴,
∴,∴
.
(2).理由如下:如图,过点F作,过点C作,
则,∴,
∵平分,平分,∴,,
∴ ,∴,
∵,∴,
∴,∴,
由①②可得,即.(3)由(2)知,,∵,
∴.
故答案为:.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
