1.5 平行线的性质 培优练习(含答案)
文档属性
| 名称 | 1.5 平行线的性质 培优练习(含答案) | 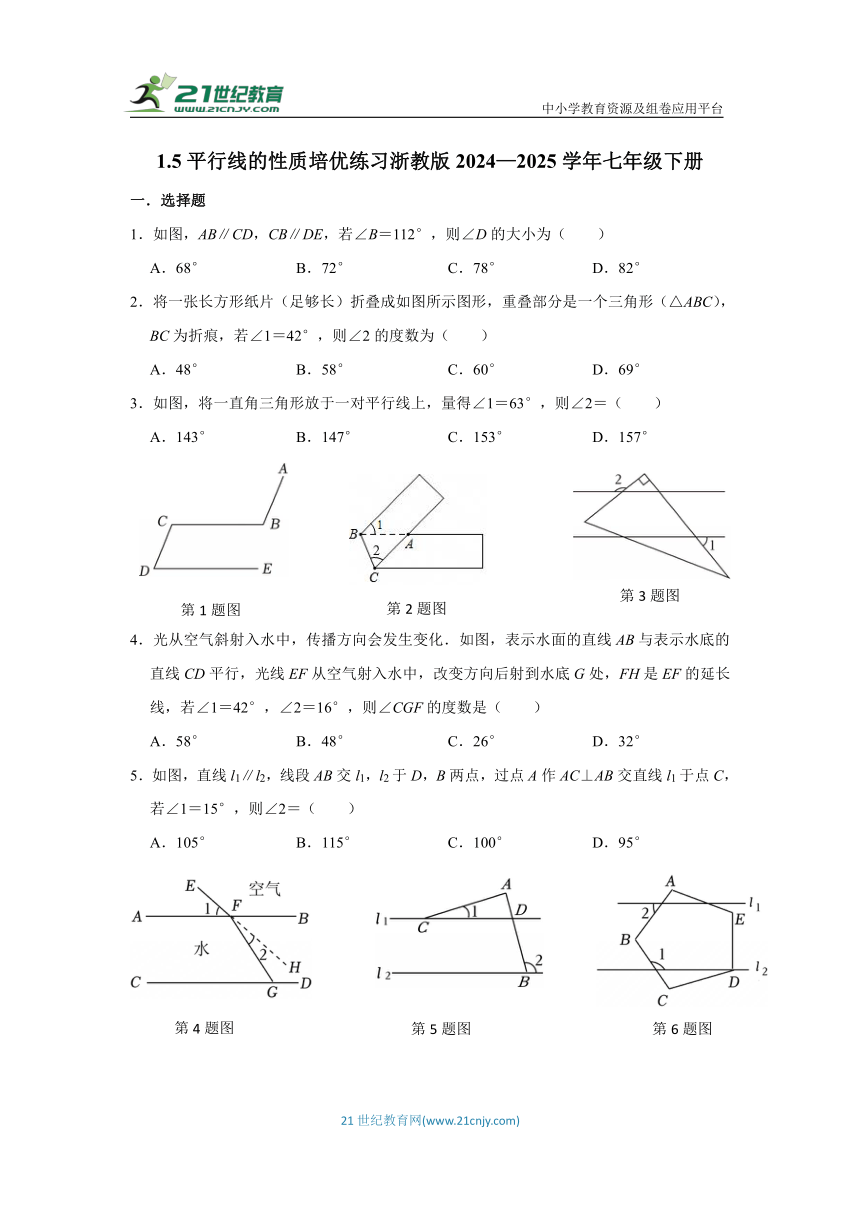 | |
| 格式 | docx | ||
| 文件大小 | 863.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 10:55:26 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
1.5平行线的性质培优练习浙教版2024—2025学年七年级下册
一.选择题
1.如图,AB∥CD,CB∥DE,若∠B=112°,则∠D的大小为( )
A.68° B.72° C.78° D.82°
2.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
3.如图,将一直角三角形放于一对平行线上,量得∠1=63°,则∠2=( )
A.143° B.147° C.153° D.157°
4.光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线AB与表示水底的直线CD平行,光线EF从空气射入水中,改变方向后射到水底G处,FH是EF的延长线,若∠1=42°,∠2=16°,则∠CGF的度数是( )
A.58° B.48° C.26° D.32°
5.如图,直线l1∥l2,线段AB交l1,l2于D,B两点,过点A作AC⊥AB交直线l1于点C,若∠1=15°,则∠2=( )
A.105° B.115° C.100° D.95°
二.填空题
6.如图,∠1﹣∠2=72°.若l1∥l2,则∠ABC= °.
7.如图,已知AB∥CD∥EF,若∠1=60°,∠3=140°,则∠2= .
8.如图,是路政工程车的工作示意图,工作篮底部AB与支撑平台CD平行.若∠1=35°,∠3=165°,则∠2的度数为 .
9.如图,AB∥CD,,,DQ,BQ分别平分∠GDE和∠HBE,则∠DFB,∠DQB满足的数量关系为: .
10.如图,一束平行主光轴EF的光线AB经凸透镜折射后,其折射光线为BF,一束光线CO经过光心O,其折射光线为OD,折射光线BF与OD交于P点,点F为焦点,若∠ABF=145°,∠COE=30°,则∠DPF= .
三.解答题
11.如图,EF∥CD,∠1=140°,∠2=40°.
(1)试说明:DG∥AC;
根据题图,在下列解答中,给①、②处填上适当的理由.
解:∵EF∥CD(已知),
∴∠1+∠ACD=180°(① ),
∵∠1=140°(已知),
∴∠ACD=40°(等式的性质),
∵∠2=40°(已知),
∴∠ACD=∠2(等量代换),
∴DG∥AC(② ).
(2)若DG平分∠CDB,求∠A的度数.
12.如图,∠AFD=∠1,AC∥DE.
(1)求证:DF∥BC;
(2)若∠1=72°,DF平分∠ADE,求∠B的度数.
13.已知AB∥CD,点E、F分别在直线AB、CD上,点M在AB、CD之间,连接ME、MF,∠EMF=α.
(1)如图1,若α=80°,直接写出∠BEM+∠DFM的度数;
(2)如图2,点N是AB上方一点,连接NE、NF,NF与ME交于点G,,,∠DFM=20°,求∠ENF的度数;(结果可用含α的式子表示)
(3)如图3,点N是AB下方一点,连接NE、NF,若MF的延长线FP是∠CFN的三等分线,EN平分∠AEM交FP于点G,2∠ENF+∠EMF=110°,求∠CFN的度数.
14.如图,点D,E分别在△ABC的边AB,AC上,点F在线段CD上,且∠DEF=∠B,DE∥BC.
(1)求证:∠BDC=∠DFE;
(2)若DE平分∠ADC,∠BDC=2∠B,求∠BDC的度数.
15.如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣8|+(b﹣2)2=0.
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动15秒,射线BQ才开始绕点B逆时针旋转,在射线BQ第一次到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?
参考答案
一、选择题
题号 1 2 3 4 5
答案 A D C A A
二、填空题
6.【解答】解:延长AB交直线l2于点F,设BC与直线l2交于点G,
∵l1∥l2,
∴∠2=∠AFG,
∵∠1是△BFG的一个外角,
∴∠FBG=∠1﹣∠AFG=∠1﹣∠2,
∵∠1﹣∠2=72°,
∴∠FBG=72°,
∴∠ABG=180°﹣∠FBG=108°,
故答案为:108.
7.【解答】解:∵AB∥EF,
∴∠BOF=∠1=60°,
∵CD∥EF,
∴∠COF=180°﹣∠3=180°﹣140°=40°,
∴∠2=∠BOF﹣∠COF=60°﹣40°=20°,
故答案为:20°.
8.【解答】解:工作篮底部AB与支撑平台CD平行,如图,过E点作EF∥AB,
∴AB∥EF∥CD,
∴∠3+∠GEF=180°,∠FEH=∠1=35°,
∴∠GEF=180°﹣∠3=180°﹣165°=15°,
∵∠GEH=∠GEF+∠FEH=15°+35°=50°,
∴路政工程车的工作示意图中∠2的度数为50°,
故答案为:50°.
9.【解答】解:过点F作FT∥CD,过点Q作QK∥AB
∵AB∥CD,
∴CD∥FT∥QK∥AB,
∴∠DFT=∠CDF,∠TFB=∠ABF,∠DQK=∠GDQ,∠KQB=∠QBH,
∴∠DFB=∠DFT+∠TFB=∠CDF+∠ABF∠DQB=∠DQK+∠KQB=∠GDQ+∠QBH,
∵,
∴,
∴,
∵DQ,BQ分别平分∠GDE和∠HBE,
∴,
∵∠GDE+∠CDE=180°,∠HBE+∠ABE=180°,
∴,
∴∴,
∴,
故答案为:.
10.【解答】解:∵AB∥EF,
∴∠ABF+∠BFE=180°.
又∵∠ABF=145°,
∴∠BFE=35°.
又∵光线CO经过光心O,且∠COE=30°,
∴∠POF=∠COE=30°,
∴∠DPF=∠BFE+∠POF=65°.
故答案为:65°.
三、解答题
11.【解答】解:(1)∵EF∥CD(已知),
∴∠1+∠ACD=180°(两直线平行,同旁内角互补),
∵∠1=140°(已知),
∴∠ACD=40°(等式的性质),
∵∠2=40°(已知),
∴∠ACD=∠2(等量代换),
∴DG∥AC(内错角相等,两直线平行).
故答案为:①两直线平行,同旁内角互补;②内错角相等,两直线平行;
(2)∵DG平分∠CDB,∠2=40°,
∴∠2=∠BDG=40°,
∵DG∥AC,
∴∠A=∠BDG=40°.
12.【解答】(1)证明:∵AC∥DE,
∴∠AFD=∠FDE,
∵∠AFD=∠1,
∴∠1=∠FDE,
∴DF∥BC;
(2)解:∵∠1=∠FDE,∠1=72°,
∴∠FDE=72°,
∵DF平分∠ADE,
∴∠FDE=∠ADF=72°,
∵DF∥BC,
∴∠B=∠ADF=72°,
∴∠B的度数为72°.
13.【解答】解:(1)如图,过M作MN∥AB,
∵AB∥CD,
∴MN∥AB∥CD,
∴∠BEM=∠NME,∠DFM=∠NMF,
∵∠EMF=α=80°,
∴∠NME+∠NMF=80°,
∴∠BEM+∠DFM=80°;
(2)∵,∠DFM=20°,
∴∠MFN=10°,∠DFN=30°,
∵∠BEM+∠DFM=α,
∴∠BEM=α﹣20°,
∵,
∴∠MEN=3∠BEM=3α﹣60°,
∴∠EGF=∠BEM+∠DFG=α﹣20°+30°=α+10,
∴∠EGN=180°﹣∠EGF=170°﹣α,
∴∠ENF=180°﹣∠MEN﹣∠EGN
=180°﹣(3α﹣60°)﹣(170°﹣α)
=70°﹣2α;
(3)方法一:∵2∠ENF+∠EMF=110°,∠EMF=α,
∴,
(Ⅰ)如图3,当时,
设∠PFN=x,则∠CFP=2x=∠DFM,∠CFN=3x,
∵∠DFM+∠BEM=∠EMF=α,
∴∠BEM=α﹣2x,
∴∠AEM=180°﹣α+2x,
∵EN平分∠AEM,
∴,
∴∠1=180°﹣∠ENF﹣∠NFP,
∵∠1+∠2=180°,
∴,
∵∠2+∠MEN+∠EMF=180°,
∴,
解得x=17.5°,
∴∠CFN=3x=52.5°;
(Ⅱ)如图4,当时,
设∠CFP=x,则∠PFN=2x,∠CFN=3x,
∴∠DFM=∠CFP=x,
∵∠MFD+∠BEM=α,
∴∠BEM=α﹣x,
∴∠AEM=180°﹣α+x,
∵EN平分∠AEM,
∴,
∵∠ENF+∠NFP+∠1=180°,
∴,
∴,
∵∠2+∠MEN+∠EMF=180°,
∴,
解得x=14°,
∴∠CFN=3x=42°;
综上,∠CFN的度数为52.5°或42°.
方法二:设∠CFN=x,
(Ⅰ)如图3,当时,
∴,
∵∠DFM+∠BEM=∠EMF=α,
∴,
∴,
∵EN平分∠AEM,
∴,
∴∠2=180°﹣∠EMF﹣∠MEN,
∵∵∠1+∠2=180°,
∴,
∴,
∵2∠ENF+∠EMF=110°,∠EMF=α,
即,
解得x=52.5°,
即∠CFN=52.5°;
(Ⅱ)如图4,当时,
∴,
∵∠DFM+∠BEM=∠EMF=α,
∴,
∴,
∵EN平分∠AEM,
∴,
∴,
∵∠1+∠2=180°,
∴,
∴,
∵2∠ENF+∠EMF=110°,∠EMF=α,
即,
解得x=42°,
即∠CFN=42°;
综上,∠CFN的度数为52.5°或42°.
14.【解答】(1)证明:∵DE∥BC,
∴∠B=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠DEF,
∴AD∥EF,
∴∠BDC=∠DFE;
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵∠ADE=∠B,
∴∠ADC=2∠B,
∵∠BDC=2∠B,∠BDC+∠ADC=180°,
∴2∠B+2∠B=180°,
∴∠B=45°,
∴∠BDC=2∠B=90°.
15.【解答】解:(1)∵|a﹣8|+(b﹣2)2=0,|a﹣8|≥0,(b﹣2)2≥0,
∴a﹣8=0,b﹣2=0,
∴a=8,b=2,
故答案为:8;2;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直,
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=180°﹣(∠ABO+∠BAO)=180°﹣90°=90°,
又∵∠OBQ=2t°,∠OAM=8t°,
∴2t+8t=90,
∴10t=90,
∴t=9,
∴至少旋转9秒时,射线AM、射线BQ互相垂直;
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动15秒后,AM转动至AM′的位置,则∠MAM′=15×8=120°,
∴∠M′AB=180°﹣45°﹣120°=15°;
分两种情况:
①当时,∠QBQ′=2t°,∠M′AM″=8t°,
∵PQ∥MN,
∴∠BAN=45°=∠ABQ,
∴∠ABQ′=45°﹣2t°,∠BAM″=∠M′AM″﹣∠M′AB=8t°﹣15°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
∴45﹣2t=8t﹣15,
∴10t=60,
解得t=6;
②当7.5<t<13.125时,∠QBQ′=2t°,∠NAM″=8(t﹣7.5)°=8t°﹣60°,
∴∠ABQ′=45°﹣2t°,∠BAM″=45°﹣(8t°﹣60°)=105°﹣8t°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
此时,45﹣2t=105﹣8t,
∴6t=60,
解得t=10;
综上所述,射线AM再转动6秒或10秒时,射线AM、射线BQ互相平行.
21世纪教育网(www.21cnjy.com)
1.5平行线的性质培优练习浙教版2024—2025学年七年级下册
一.选择题
1.如图,AB∥CD,CB∥DE,若∠B=112°,则∠D的大小为( )
A.68° B.72° C.78° D.82°
2.将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形(△ABC),BC为折痕,若∠1=42°,则∠2的度数为( )
A.48° B.58° C.60° D.69°
3.如图,将一直角三角形放于一对平行线上,量得∠1=63°,则∠2=( )
A.143° B.147° C.153° D.157°
4.光从空气斜射入水中,传播方向会发生变化.如图,表示水面的直线AB与表示水底的直线CD平行,光线EF从空气射入水中,改变方向后射到水底G处,FH是EF的延长线,若∠1=42°,∠2=16°,则∠CGF的度数是( )
A.58° B.48° C.26° D.32°
5.如图,直线l1∥l2,线段AB交l1,l2于D,B两点,过点A作AC⊥AB交直线l1于点C,若∠1=15°,则∠2=( )
A.105° B.115° C.100° D.95°
二.填空题
6.如图,∠1﹣∠2=72°.若l1∥l2,则∠ABC= °.
7.如图,已知AB∥CD∥EF,若∠1=60°,∠3=140°,则∠2= .
8.如图,是路政工程车的工作示意图,工作篮底部AB与支撑平台CD平行.若∠1=35°,∠3=165°,则∠2的度数为 .
9.如图,AB∥CD,,,DQ,BQ分别平分∠GDE和∠HBE,则∠DFB,∠DQB满足的数量关系为: .
10.如图,一束平行主光轴EF的光线AB经凸透镜折射后,其折射光线为BF,一束光线CO经过光心O,其折射光线为OD,折射光线BF与OD交于P点,点F为焦点,若∠ABF=145°,∠COE=30°,则∠DPF= .
三.解答题
11.如图,EF∥CD,∠1=140°,∠2=40°.
(1)试说明:DG∥AC;
根据题图,在下列解答中,给①、②处填上适当的理由.
解:∵EF∥CD(已知),
∴∠1+∠ACD=180°(① ),
∵∠1=140°(已知),
∴∠ACD=40°(等式的性质),
∵∠2=40°(已知),
∴∠ACD=∠2(等量代换),
∴DG∥AC(② ).
(2)若DG平分∠CDB,求∠A的度数.
12.如图,∠AFD=∠1,AC∥DE.
(1)求证:DF∥BC;
(2)若∠1=72°,DF平分∠ADE,求∠B的度数.
13.已知AB∥CD,点E、F分别在直线AB、CD上,点M在AB、CD之间,连接ME、MF,∠EMF=α.
(1)如图1,若α=80°,直接写出∠BEM+∠DFM的度数;
(2)如图2,点N是AB上方一点,连接NE、NF,NF与ME交于点G,,,∠DFM=20°,求∠ENF的度数;(结果可用含α的式子表示)
(3)如图3,点N是AB下方一点,连接NE、NF,若MF的延长线FP是∠CFN的三等分线,EN平分∠AEM交FP于点G,2∠ENF+∠EMF=110°,求∠CFN的度数.
14.如图,点D,E分别在△ABC的边AB,AC上,点F在线段CD上,且∠DEF=∠B,DE∥BC.
(1)求证:∠BDC=∠DFE;
(2)若DE平分∠ADC,∠BDC=2∠B,求∠BDC的度数.
15.如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣8|+(b﹣2)2=0.
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动15秒,射线BQ才开始绕点B逆时针旋转,在射线BQ第一次到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?
参考答案
一、选择题
题号 1 2 3 4 5
答案 A D C A A
二、填空题
6.【解答】解:延长AB交直线l2于点F,设BC与直线l2交于点G,
∵l1∥l2,
∴∠2=∠AFG,
∵∠1是△BFG的一个外角,
∴∠FBG=∠1﹣∠AFG=∠1﹣∠2,
∵∠1﹣∠2=72°,
∴∠FBG=72°,
∴∠ABG=180°﹣∠FBG=108°,
故答案为:108.
7.【解答】解:∵AB∥EF,
∴∠BOF=∠1=60°,
∵CD∥EF,
∴∠COF=180°﹣∠3=180°﹣140°=40°,
∴∠2=∠BOF﹣∠COF=60°﹣40°=20°,
故答案为:20°.
8.【解答】解:工作篮底部AB与支撑平台CD平行,如图,过E点作EF∥AB,
∴AB∥EF∥CD,
∴∠3+∠GEF=180°,∠FEH=∠1=35°,
∴∠GEF=180°﹣∠3=180°﹣165°=15°,
∵∠GEH=∠GEF+∠FEH=15°+35°=50°,
∴路政工程车的工作示意图中∠2的度数为50°,
故答案为:50°.
9.【解答】解:过点F作FT∥CD,过点Q作QK∥AB
∵AB∥CD,
∴CD∥FT∥QK∥AB,
∴∠DFT=∠CDF,∠TFB=∠ABF,∠DQK=∠GDQ,∠KQB=∠QBH,
∴∠DFB=∠DFT+∠TFB=∠CDF+∠ABF∠DQB=∠DQK+∠KQB=∠GDQ+∠QBH,
∵,
∴,
∴,
∵DQ,BQ分别平分∠GDE和∠HBE,
∴,
∵∠GDE+∠CDE=180°,∠HBE+∠ABE=180°,
∴,
∴∴,
∴,
故答案为:.
10.【解答】解:∵AB∥EF,
∴∠ABF+∠BFE=180°.
又∵∠ABF=145°,
∴∠BFE=35°.
又∵光线CO经过光心O,且∠COE=30°,
∴∠POF=∠COE=30°,
∴∠DPF=∠BFE+∠POF=65°.
故答案为:65°.
三、解答题
11.【解答】解:(1)∵EF∥CD(已知),
∴∠1+∠ACD=180°(两直线平行,同旁内角互补),
∵∠1=140°(已知),
∴∠ACD=40°(等式的性质),
∵∠2=40°(已知),
∴∠ACD=∠2(等量代换),
∴DG∥AC(内错角相等,两直线平行).
故答案为:①两直线平行,同旁内角互补;②内错角相等,两直线平行;
(2)∵DG平分∠CDB,∠2=40°,
∴∠2=∠BDG=40°,
∵DG∥AC,
∴∠A=∠BDG=40°.
12.【解答】(1)证明:∵AC∥DE,
∴∠AFD=∠FDE,
∵∠AFD=∠1,
∴∠1=∠FDE,
∴DF∥BC;
(2)解:∵∠1=∠FDE,∠1=72°,
∴∠FDE=72°,
∵DF平分∠ADE,
∴∠FDE=∠ADF=72°,
∵DF∥BC,
∴∠B=∠ADF=72°,
∴∠B的度数为72°.
13.【解答】解:(1)如图,过M作MN∥AB,
∵AB∥CD,
∴MN∥AB∥CD,
∴∠BEM=∠NME,∠DFM=∠NMF,
∵∠EMF=α=80°,
∴∠NME+∠NMF=80°,
∴∠BEM+∠DFM=80°;
(2)∵,∠DFM=20°,
∴∠MFN=10°,∠DFN=30°,
∵∠BEM+∠DFM=α,
∴∠BEM=α﹣20°,
∵,
∴∠MEN=3∠BEM=3α﹣60°,
∴∠EGF=∠BEM+∠DFG=α﹣20°+30°=α+10,
∴∠EGN=180°﹣∠EGF=170°﹣α,
∴∠ENF=180°﹣∠MEN﹣∠EGN
=180°﹣(3α﹣60°)﹣(170°﹣α)
=70°﹣2α;
(3)方法一:∵2∠ENF+∠EMF=110°,∠EMF=α,
∴,
(Ⅰ)如图3,当时,
设∠PFN=x,则∠CFP=2x=∠DFM,∠CFN=3x,
∵∠DFM+∠BEM=∠EMF=α,
∴∠BEM=α﹣2x,
∴∠AEM=180°﹣α+2x,
∵EN平分∠AEM,
∴,
∴∠1=180°﹣∠ENF﹣∠NFP,
∵∠1+∠2=180°,
∴,
∵∠2+∠MEN+∠EMF=180°,
∴,
解得x=17.5°,
∴∠CFN=3x=52.5°;
(Ⅱ)如图4,当时,
设∠CFP=x,则∠PFN=2x,∠CFN=3x,
∴∠DFM=∠CFP=x,
∵∠MFD+∠BEM=α,
∴∠BEM=α﹣x,
∴∠AEM=180°﹣α+x,
∵EN平分∠AEM,
∴,
∵∠ENF+∠NFP+∠1=180°,
∴,
∴,
∵∠2+∠MEN+∠EMF=180°,
∴,
解得x=14°,
∴∠CFN=3x=42°;
综上,∠CFN的度数为52.5°或42°.
方法二:设∠CFN=x,
(Ⅰ)如图3,当时,
∴,
∵∠DFM+∠BEM=∠EMF=α,
∴,
∴,
∵EN平分∠AEM,
∴,
∴∠2=180°﹣∠EMF﹣∠MEN,
∵∵∠1+∠2=180°,
∴,
∴,
∵2∠ENF+∠EMF=110°,∠EMF=α,
即,
解得x=52.5°,
即∠CFN=52.5°;
(Ⅱ)如图4,当时,
∴,
∵∠DFM+∠BEM=∠EMF=α,
∴,
∴,
∵EN平分∠AEM,
∴,
∴,
∵∠1+∠2=180°,
∴,
∴,
∵2∠ENF+∠EMF=110°,∠EMF=α,
即,
解得x=42°,
即∠CFN=42°;
综上,∠CFN的度数为52.5°或42°.
14.【解答】(1)证明:∵DE∥BC,
∴∠B=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠DEF,
∴AD∥EF,
∴∠BDC=∠DFE;
(2)解:∵DE平分∠ADC,
∴∠ADC=2∠ADE,
∵∠ADE=∠B,
∴∠ADC=2∠B,
∵∠BDC=2∠B,∠BDC+∠ADC=180°,
∴2∠B+2∠B=180°,
∴∠B=45°,
∴∠BDC=2∠B=90°.
15.【解答】解:(1)∵|a﹣8|+(b﹣2)2=0,|a﹣8|≥0,(b﹣2)2≥0,
∴a﹣8=0,b﹣2=0,
∴a=8,b=2,
故答案为:8;2;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直,
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=180°﹣(∠ABO+∠BAO)=180°﹣90°=90°,
又∵∠OBQ=2t°,∠OAM=8t°,
∴2t+8t=90,
∴10t=90,
∴t=9,
∴至少旋转9秒时,射线AM、射线BQ互相垂直;
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动15秒后,AM转动至AM′的位置,则∠MAM′=15×8=120°,
∴∠M′AB=180°﹣45°﹣120°=15°;
分两种情况:
①当时,∠QBQ′=2t°,∠M′AM″=8t°,
∵PQ∥MN,
∴∠BAN=45°=∠ABQ,
∴∠ABQ′=45°﹣2t°,∠BAM″=∠M′AM″﹣∠M′AB=8t°﹣15°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
∴45﹣2t=8t﹣15,
∴10t=60,
解得t=6;
②当7.5<t<13.125时,∠QBQ′=2t°,∠NAM″=8(t﹣7.5)°=8t°﹣60°,
∴∠ABQ′=45°﹣2t°,∠BAM″=45°﹣(8t°﹣60°)=105°﹣8t°,
当∠ABQ′=∠BAM″时,BQ′∥AM″,
此时,45﹣2t=105﹣8t,
∴6t=60,
解得t=10;
综上所述,射线AM再转动6秒或10秒时,射线AM、射线BQ互相平行.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
