第一章相交线与平行线单元测试(含答案)
文档属性
| 名称 | 第一章相交线与平行线单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 732.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章相交线与平行线单元测试浙教版2024—2025学年七年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.在同一平面内有两条相交直线与另外一条直线,它们的交点的个数是( )
A.1 B.2 C.3或2 D.1或2或3
2.如图,直线AB,CD相交于点O.若∠1=40°,∠2=120°,则∠COM的度数为( )
A.70° B.80° C.90° D.100°
3.如图,推动水桶,以点O为支点,使其向右倾斜.若在点A处分别施加推力F1、F2,则F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是( )
A.垂线段最短
B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线
D.过直线外一点有且只有一条直线与已知直线平行
4.如图,AB∥CD,AD平分∠BAC,∠1=30°,则∠2=( )
A.15° B.30° C.45° D.60°
5.把一块含30°角的直角三角板按如图方式放置于两条平行线间,若∠1=45°,则∠2=( )
A.10° B.15° C.20° D.30°
6.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180°
C.∠4=∠5 D.∠1=∠2
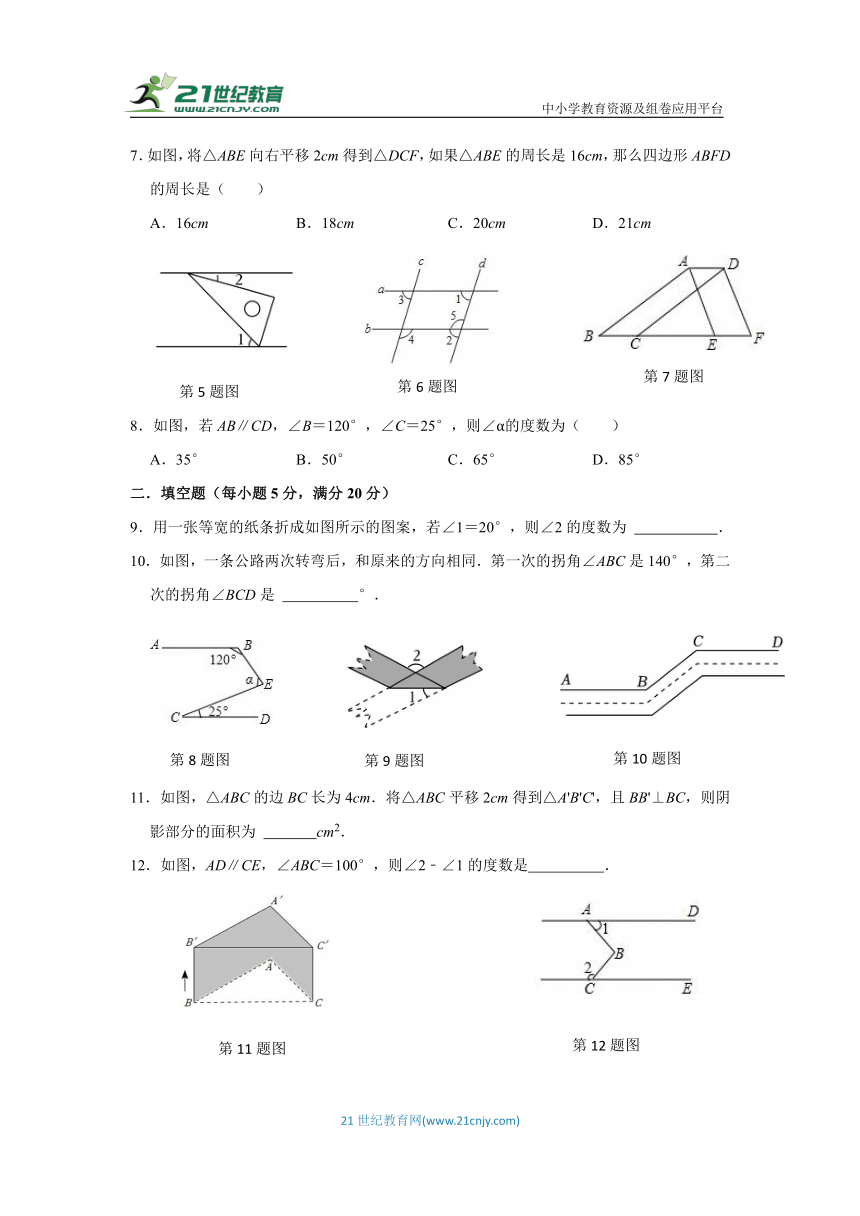
7.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
8.如图,若AB∥CD,∠B=120°,∠C=25°,则∠α的度数为( )
A.35° B.50° C.65° D.85°
二.填空题(每小题5分,满分20分)
9.用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
10.如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC是140°,第二次的拐角∠BCD是 °.
11.如图,△ABC的边BC长为4cm.将△ABC平移2cm得到△A'B'C',且BB'⊥BC,则阴影部分的面积为 cm2.
12.如图,AD∥CE,∠ABC=100°,则∠2﹣∠1的度数是 .
三.解答题(共6小题,每小题10分,每题须有必要的文字说明和解答过程)
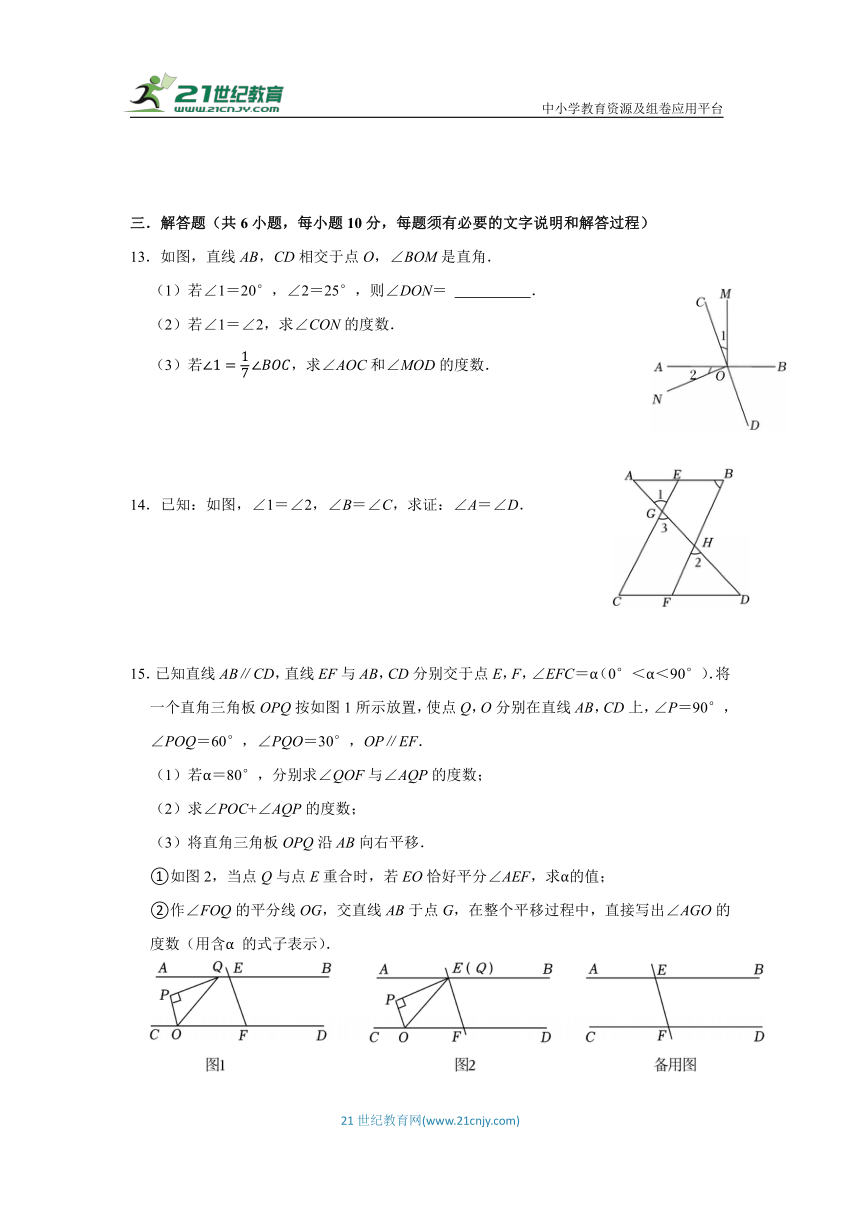
13.如图,直线AB,CD相交于点O,∠BOM是直角.
(1)若∠1=20°,∠2=25°,则∠DON= .
(2)若∠1=∠2,求∠CON的度数.
(3)若,求∠AOC和∠MOD的度数.
14.已知:如图,∠1=∠2,∠B=∠C,求证:∠A=∠D.
15.已知直线AB∥CD,直线EF与AB,CD分别交于点E,F,∠EFC=α(0°<α<90°).将一个直角三角板OPQ按如图1所示放置,使点Q,O分别在直线AB,CD上,∠P=90°,∠POQ=60°,∠PQO=30°,OP∥EF.
(1)若α=80°,分别求∠QOF与∠AQP的度数;
(2)求∠POC+∠AQP的度数;
(3)将直角三角板OPQ沿AB向右平移.
①如图2,当点Q与点E重合时,若EO恰好平分∠AEF,求α的值;
②作∠FOQ的平分线OG,交直线AB于点G,在整个平移过程中,直接写出∠AGO的度数(用含α 的式子表示).
16.如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?
(2)若∠ABD=25°时,求∠DBE的度数;
(3)若平行移动AD,在平行移动AD的过程中,是否存在某一位置,使∠BEC=∠ADB?若存在,请直接写出∠ADB的度数;若不存在,请说明理由.
17.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
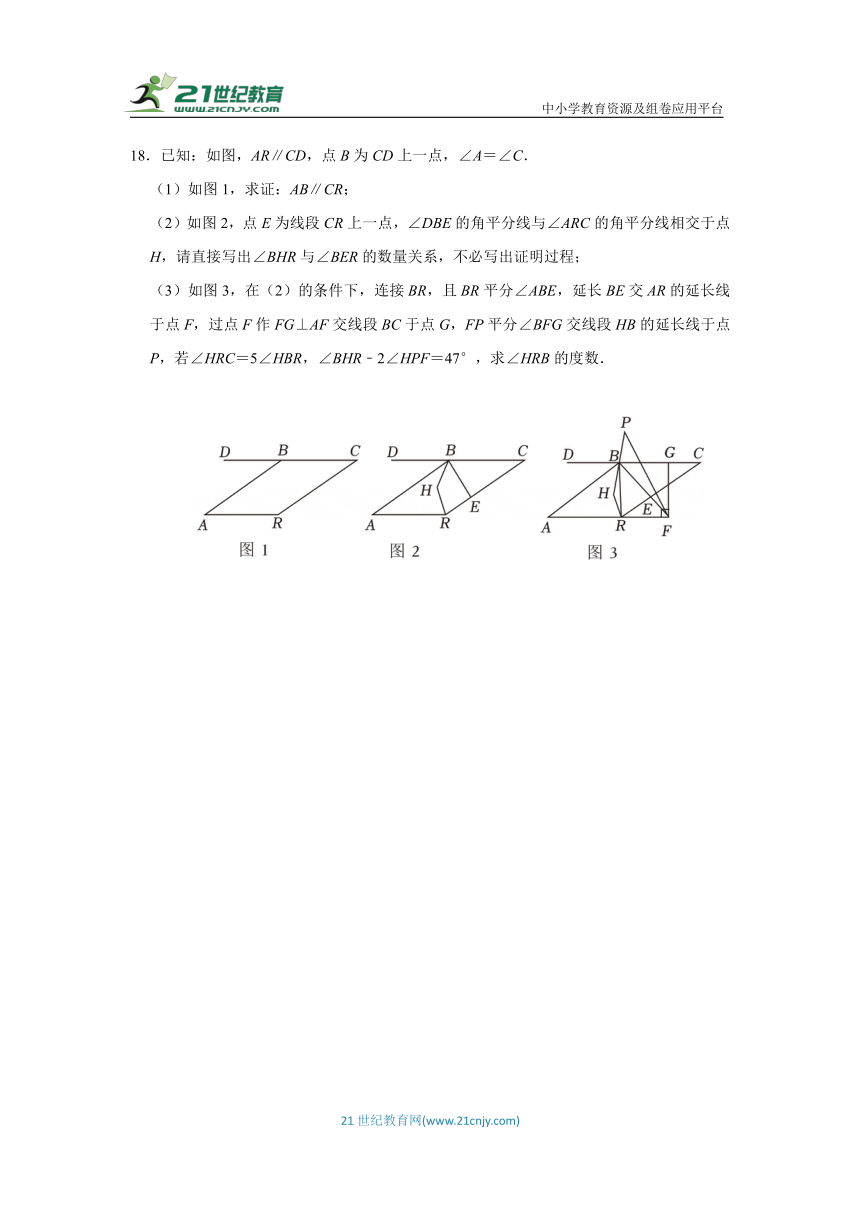
18.已知:如图,AR∥CD,点B为CD上一点,∠A=∠C.
(1)如图1,求证:AB∥CR;
(2)如图2,点E为线段CR上一点,∠DBE的角平分线与∠ARC的角平分线相交于点H,请直接写出∠BHR与∠BER的数量关系,不必写出证明过程;
(3)如图3,在(2)的条件下,连接BR,且BR平分∠ABE,延长BE交AR的延长线于点F,过点F作FG⊥AF交线段BC于点G,FP平分∠BFG交线段HB的延长线于点P,若∠HRC=5∠HBR,∠BHR﹣2∠HPF=47°,求∠HRB的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D B A B B D C D
二、填空题
9.【解答】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180°﹣∠ABC﹣∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20°,
∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.
故答案为:140°.
10.【解答】解:∵道路是平行的,
∴∠ABC=∠BCD=140°(两直线平行,内错角相等).
故答案为:140.
11.【解答】解:由平移可知,阴影部分的面积等于四边形BB'C'C的面积=BC×BB'=4×2=8(cm2),
故答案为:8.
12.【解答】解:作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,
∴∠1+∠4=100°,∠2+∠4=180°,
∴∠2﹣∠1=80°.
故答案为:80°.
三、解答题
13.【解答】解:(1)根据题意可知,∠BOM=90°,
∴∠AOM=90°,
∵∠1=20°,
∴∠AOC=90°﹣∠1=90°﹣20°=70°,
∵∠2=25°,
∴∠BON=180°﹣∠AOC﹣∠2=180°﹣70°﹣25°=85°;
故答案为:85°;
(2)∵∠1=∠2,∠AOM=90°,
∴∠CON=∠2+∠AOC=∠1+∠AOC=90°;
(3)∵,∠BOM=90°,
∴,
∴∠AOC=90°﹣∠1=75°,
∴∠BOD=75°,
∴∠MOD=∠BOM+∠BOD=165°.
14.【解答】证明:根据题意可知,∠1=∠3,∠1=∠2,
∴∠3=∠2(等量代换),
∴EC∥BF,
∴根据平行线的性质,∠AEC=∠B,
∵∠B=∠C,
∴∠AEC=∠C,
∴AB∥CD,
∴∠A=∠D.
15.【解答】解:(1)如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∴∠OPQ=∠OPM+∠QOM=90°,
∵OP∥EF,
∴∠EFC=∠POC=α=80°,
∴∠AQP=90°﹣80°=10°,
∵AB∥CD,
∴∠QOF=∠AQO=∠AQP+∠PQO=10°+30°=40°,
即∠QOF=40°,∠AQP=10°;
(2)∠POC+∠AQP=90°,
如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∵∠OPQ=∠OPM+∠QOM=90°,
∴∠POC+∠AQP=90°;
(3)①如图2,∵EO恰好平分∠AEF,
∴∠AEO=∠OEF,
∵AB∥CD,
∴∠AEO=∠EOF=∠OEF,
∵OP∥EF,
∴∠POC=∠EFC=α,
∴∠EOF=180°﹣60°﹣α,
在△EOF中,由内角和定理可得,
∠EOF+∠OEF+∠OFE=180°,
即2×(180°﹣60°﹣α)+α=180°,
解得α=60°;
②如图1,∠AGO=∠GOF∠FOQ,
∵∠FOQ=180°﹣60°﹣α=120°﹣α,
∴∠AGO(120°﹣α)=60°α;
如图3,∵PO∥EF,
∴∠POF=∠EFC=α,
∴∠QOF=60°+α,
∵OG平分∠QOF,
∴∠GOF∠QOF=30°α,
∵AB∥CD,
∴∠AGO=180°﹣∠GOF=150°α,
综上所述∠AGO=150°α或∠AGO=60°α.
16.【解答】解:(1)AD∥BC,理由如下:
∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE∠ABF∠CBF∠ABC=40°;
(3)存在,理由如下:
设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
17.【解答】解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
18.【解答】(1)证明:∵AR∥CD,
∴∠A=∠ABD,
∵∠A=∠C,
∴∠C=∠ABD,
∴AB∥CR;
(2)解:2∠BHR+∠BER=360°,理由如下:
如图:分别过点E,H作AR的平行线PQ,MN,
∵AR∥CD,AR∥PQ,AR∥MN,
∴AR∥MN∥PQ∥CD,
设∠ABD=x,∠ABH=y,则∠HBD=x+y,
∴∠C=x,∠BHN=x+y,
∴∠ARC=180°﹣x,∠PER=x,
∵BH平分∠DBE,RH平分∠ARC,
∴,
∴,
∴∠BEP=∠CBE=180°﹣2x﹣2y,
∴∠BEP=∠CBE=180°﹣2x﹣2y
∴,
∵2∠BHR=180°+x+2y,
∴2∠BHR+∠BER=180°+x+2y+180°﹣x﹣2y=360°;
(3)解:设∠HBR=α,∠ABH=β,则∠ABR=α+β,
∵BR平分∠ABE,
∴∠EBR=∠ABR=α+β,
∴∠HBE=∠HBR+∠EBR=2α+β,
∵BH平分∠DBE,
∴∠DBH=∠HBE=2α+β,
∴∠ABD=∠DBH﹣∠ABH=2α,
∴∠C=∠ABD=2α,
∵∠HRC=5∠HBR,
∴∠HRC=5α,
∵RH平分∠ARC,
∴∠ARH=∠HRC=5α,
∴∠CRF=180°﹣10α,
∵AR∥CD,
∴∠C=∠CRF,即2α=180°﹣10α,
∴α=15°,
∴∠C=∠CRF=30°,∠ARH=∠HRC=5α=75°,∠CBE=180°﹣2∠DBH=180°﹣4α﹣2β=120°﹣2β,
∴∠C=∠CRF=30°,
如图,过点P作PK∥CD,过点H作ST∥CD,
∴∠DBH=∠THB=2α+β=30°+β,∠THR=∠ARH=75°,
∴∠BHR=∠DBH+∠ARH=7α+β=105°+β,
∵∠CBH=180°﹣∠DBH=180°﹣2α﹣β=150°﹣β,
∴∠KPB=∠CBH=150°﹣β,
∵FG⊥AF,
∴∠AFG=90°,
∵AR∥CD,
∴∠CBE=∠AFB=120°﹣2β,
∴∠BFG=∠AFG﹣∠AFB=90°﹣(120°﹣2β)=2β﹣30°,
∵FP平分∠BFG,
∴,
∵AR∥CD,PK∥CD,
∴AR∥PK,
∴∠KPF=∠AFP=∠AFB+∠PFB=105°﹣β,
∴∠HPF=∠KPB﹣∠KPF=45°,
∵∠BHR﹣2∠HPF=47°,
∴105°+β﹣2×45°=47°,
∴β=32°,
∴∠DBR=∠DBH+∠HBR=2α+β+α=77°,
∴∠ARB=180°﹣∠DBR=180°﹣77°=103°,
∵∠ARH=75°,
∴∠HRB=∠ARB﹣∠ARH=103°﹣75°=28°,
所以∠HRB的度数为28°.
21世纪教育网(www.21cnjy.com)
第一章相交线与平行线单元测试浙教版2024—2025学年七年级下册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题5分,满分40分)
题号 1 3 4 5 6 7 8
答案
1.在同一平面内有两条相交直线与另外一条直线,它们的交点的个数是( )
A.1 B.2 C.3或2 D.1或2或3
2.如图,直线AB,CD相交于点O.若∠1=40°,∠2=120°,则∠COM的度数为( )
A.70° B.80° C.90° D.100°
3.如图,推动水桶,以点O为支点,使其向右倾斜.若在点A处分别施加推力F1、F2,则F1的力臂OA大于F2的力臂OB.这一判断过程体现的数学依据是( )
A.垂线段最短
B.过一点有且只有一条直线与已知直线垂直
C.两点确定一条直线
D.过直线外一点有且只有一条直线与已知直线平行
4.如图,AB∥CD,AD平分∠BAC,∠1=30°,则∠2=( )
A.15° B.30° C.45° D.60°
5.把一块含30°角的直角三角板按如图方式放置于两条平行线间,若∠1=45°,则∠2=( )
A.10° B.15° C.20° D.30°
6.如图,直线a,b被直线c,d所截.下列条件能判定a∥b的是( )
A.∠1=∠3 B.∠2+∠4=180°
C.∠4=∠5 D.∠1=∠2
7.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
8.如图,若AB∥CD,∠B=120°,∠C=25°,则∠α的度数为( )
A.35° B.50° C.65° D.85°
二.填空题(每小题5分,满分20分)
9.用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
10.如图,一条公路两次转弯后,和原来的方向相同.第一次的拐角∠ABC是140°,第二次的拐角∠BCD是 °.
11.如图,△ABC的边BC长为4cm.将△ABC平移2cm得到△A'B'C',且BB'⊥BC,则阴影部分的面积为 cm2.
12.如图,AD∥CE,∠ABC=100°,则∠2﹣∠1的度数是 .
三.解答题(共6小题,每小题10分,每题须有必要的文字说明和解答过程)
13.如图,直线AB,CD相交于点O,∠BOM是直角.
(1)若∠1=20°,∠2=25°,则∠DON= .
(2)若∠1=∠2,求∠CON的度数.
(3)若,求∠AOC和∠MOD的度数.
14.已知:如图,∠1=∠2,∠B=∠C,求证:∠A=∠D.
15.已知直线AB∥CD,直线EF与AB,CD分别交于点E,F,∠EFC=α(0°<α<90°).将一个直角三角板OPQ按如图1所示放置,使点Q,O分别在直线AB,CD上,∠P=90°,∠POQ=60°,∠PQO=30°,OP∥EF.
(1)若α=80°,分别求∠QOF与∠AQP的度数;
(2)求∠POC+∠AQP的度数;
(3)将直角三角板OPQ沿AB向右平移.
①如图2,当点Q与点E重合时,若EO恰好平分∠AEF,求α的值;
②作∠FOQ的平分线OG,交直线AB于点G,在整个平移过程中,直接写出∠AGO的度数(用含α 的式子表示).
16.如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?
(2)若∠ABD=25°时,求∠DBE的度数;
(3)若平行移动AD,在平行移动AD的过程中,是否存在某一位置,使∠BEC=∠ADB?若存在,请直接写出∠ADB的度数;若不存在,请说明理由.
17.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
18.已知:如图,AR∥CD,点B为CD上一点,∠A=∠C.
(1)如图1,求证:AB∥CR;
(2)如图2,点E为线段CR上一点,∠DBE的角平分线与∠ARC的角平分线相交于点H,请直接写出∠BHR与∠BER的数量关系,不必写出证明过程;
(3)如图3,在(2)的条件下,连接BR,且BR平分∠ABE,延长BE交AR的延长线于点F,过点F作FG⊥AF交线段BC于点G,FP平分∠BFG交线段HB的延长线于点P,若∠HRC=5∠HBR,∠BHR﹣2∠HPF=47°,求∠HRB的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D B A B B D C D
二、填空题
9.【解答】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180°﹣∠ABC﹣∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20°,
∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.
故答案为:140°.
10.【解答】解:∵道路是平行的,
∴∠ABC=∠BCD=140°(两直线平行,内错角相等).
故答案为:140.
11.【解答】解:由平移可知,阴影部分的面积等于四边形BB'C'C的面积=BC×BB'=4×2=8(cm2),
故答案为:8.
12.【解答】解:作BF∥AD,
∵AD∥CE,
∴AD∥BF∥EC,
∴∠1=∠3,∠4+∠2=180°,∠3+∠4=100°,
∴∠1+∠4=100°,∠2+∠4=180°,
∴∠2﹣∠1=80°.
故答案为:80°.
三、解答题
13.【解答】解:(1)根据题意可知,∠BOM=90°,
∴∠AOM=90°,
∵∠1=20°,
∴∠AOC=90°﹣∠1=90°﹣20°=70°,
∵∠2=25°,
∴∠BON=180°﹣∠AOC﹣∠2=180°﹣70°﹣25°=85°;
故答案为:85°;
(2)∵∠1=∠2,∠AOM=90°,
∴∠CON=∠2+∠AOC=∠1+∠AOC=90°;
(3)∵,∠BOM=90°,
∴,
∴∠AOC=90°﹣∠1=75°,
∴∠BOD=75°,
∴∠MOD=∠BOM+∠BOD=165°.
14.【解答】证明:根据题意可知,∠1=∠3,∠1=∠2,
∴∠3=∠2(等量代换),
∴EC∥BF,
∴根据平行线的性质,∠AEC=∠B,
∵∠B=∠C,
∴∠AEC=∠C,
∴AB∥CD,
∴∠A=∠D.
15.【解答】解:(1)如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∴∠OPQ=∠OPM+∠QOM=90°,
∵OP∥EF,
∴∠EFC=∠POC=α=80°,
∴∠AQP=90°﹣80°=10°,
∵AB∥CD,
∴∠QOF=∠AQO=∠AQP+∠PQO=10°+30°=40°,
即∠QOF=40°,∠AQP=10°;
(2)∠POC+∠AQP=90°,
如图1,过点P作PM∥AB,
∵AB∥CD,
∴AB∥CD∥PM,
∴∠AQP=∠QPM,∠POC=∠MPO,
∵∠OPQ=∠OPM+∠QOM=90°,
∴∠POC+∠AQP=90°;
(3)①如图2,∵EO恰好平分∠AEF,
∴∠AEO=∠OEF,
∵AB∥CD,
∴∠AEO=∠EOF=∠OEF,
∵OP∥EF,
∴∠POC=∠EFC=α,
∴∠EOF=180°﹣60°﹣α,
在△EOF中,由内角和定理可得,
∠EOF+∠OEF+∠OFE=180°,
即2×(180°﹣60°﹣α)+α=180°,
解得α=60°;
②如图1,∠AGO=∠GOF∠FOQ,
∵∠FOQ=180°﹣60°﹣α=120°﹣α,
∴∠AGO(120°﹣α)=60°α;
如图3,∵PO∥EF,
∴∠POF=∠EFC=α,
∴∠QOF=60°+α,
∵OG平分∠QOF,
∴∠GOF∠QOF=30°α,
∵AB∥CD,
∴∠AGO=180°﹣∠GOF=150°α,
综上所述∠AGO=150°α或∠AGO=60°α.
16.【解答】解:(1)AD∥BC,理由如下:
∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE∠ABF∠CBF∠ABC=40°;
(3)存在,理由如下:
设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
17.【解答】解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
18.【解答】(1)证明:∵AR∥CD,
∴∠A=∠ABD,
∵∠A=∠C,
∴∠C=∠ABD,
∴AB∥CR;
(2)解:2∠BHR+∠BER=360°,理由如下:
如图:分别过点E,H作AR的平行线PQ,MN,
∵AR∥CD,AR∥PQ,AR∥MN,
∴AR∥MN∥PQ∥CD,
设∠ABD=x,∠ABH=y,则∠HBD=x+y,
∴∠C=x,∠BHN=x+y,
∴∠ARC=180°﹣x,∠PER=x,
∵BH平分∠DBE,RH平分∠ARC,
∴,
∴,
∴∠BEP=∠CBE=180°﹣2x﹣2y,
∴∠BEP=∠CBE=180°﹣2x﹣2y
∴,
∵2∠BHR=180°+x+2y,
∴2∠BHR+∠BER=180°+x+2y+180°﹣x﹣2y=360°;
(3)解:设∠HBR=α,∠ABH=β,则∠ABR=α+β,
∵BR平分∠ABE,
∴∠EBR=∠ABR=α+β,
∴∠HBE=∠HBR+∠EBR=2α+β,
∵BH平分∠DBE,
∴∠DBH=∠HBE=2α+β,
∴∠ABD=∠DBH﹣∠ABH=2α,
∴∠C=∠ABD=2α,
∵∠HRC=5∠HBR,
∴∠HRC=5α,
∵RH平分∠ARC,
∴∠ARH=∠HRC=5α,
∴∠CRF=180°﹣10α,
∵AR∥CD,
∴∠C=∠CRF,即2α=180°﹣10α,
∴α=15°,
∴∠C=∠CRF=30°,∠ARH=∠HRC=5α=75°,∠CBE=180°﹣2∠DBH=180°﹣4α﹣2β=120°﹣2β,
∴∠C=∠CRF=30°,
如图,过点P作PK∥CD,过点H作ST∥CD,
∴∠DBH=∠THB=2α+β=30°+β,∠THR=∠ARH=75°,
∴∠BHR=∠DBH+∠ARH=7α+β=105°+β,
∵∠CBH=180°﹣∠DBH=180°﹣2α﹣β=150°﹣β,
∴∠KPB=∠CBH=150°﹣β,
∵FG⊥AF,
∴∠AFG=90°,
∵AR∥CD,
∴∠CBE=∠AFB=120°﹣2β,
∴∠BFG=∠AFG﹣∠AFB=90°﹣(120°﹣2β)=2β﹣30°,
∵FP平分∠BFG,
∴,
∵AR∥CD,PK∥CD,
∴AR∥PK,
∴∠KPF=∠AFP=∠AFB+∠PFB=105°﹣β,
∴∠HPF=∠KPB﹣∠KPF=45°,
∵∠BHR﹣2∠HPF=47°,
∴105°+β﹣2×45°=47°,
∴β=32°,
∴∠DBR=∠DBH+∠HBR=2α+β+α=77°,
∴∠ARB=180°﹣∠DBR=180°﹣77°=103°,
∵∠ARH=75°,
∴∠HRB=∠ARB﹣∠ARH=103°﹣75°=28°,
所以∠HRB的度数为28°.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
