第三章整式的乘除单元测试（含答案）

中小学教育资源及组卷应用平台
第三章整式的乘除单元测试浙教版2024—2025学年七年级下册
总分：120分 时间：90分钟
姓名：________ 班级：_____________成绩：___________
一．单项选择题（每小题5分，满分40分）
题号 1 3 4 5 6 7 8
答案
1．计算的结果等于（　　）
A．﹣5 B．5 C． D．
2．若3m﹣n﹣2＝0，则8m÷2n的值是（　　）
A．0 B．1 C．2 D．4
3．已知（a+b）2＝9，ab，则（a﹣b）2的值为（　　）
A．9 B．3 C．12 D．6
4．如图①，从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后，将剩余的部分剪拼成一个长方形，如图②．通过计算阴影部分的面积可以得到（　　）
A．（a﹣2b）2＝a2﹣4ab+b2
B．（a﹣b）（a+2b）＝a2+ab﹣2b2
C．（a﹣2b）（a+2b）＝a2﹣4b2
D．（a+b）（a﹣b）＝a2﹣b2
5．若将（2x+a）（2x﹣b）展开的结果中不含有x项，则a，b满足的关系式是（　　）
A．ab＝1 B．ab＝0 C．a﹣b＝0 D．a+b＝0
6．已知xm＝6，xn＝4，则x2m﹣n的值为（　　）
A．8 B．9 C．10 D．12
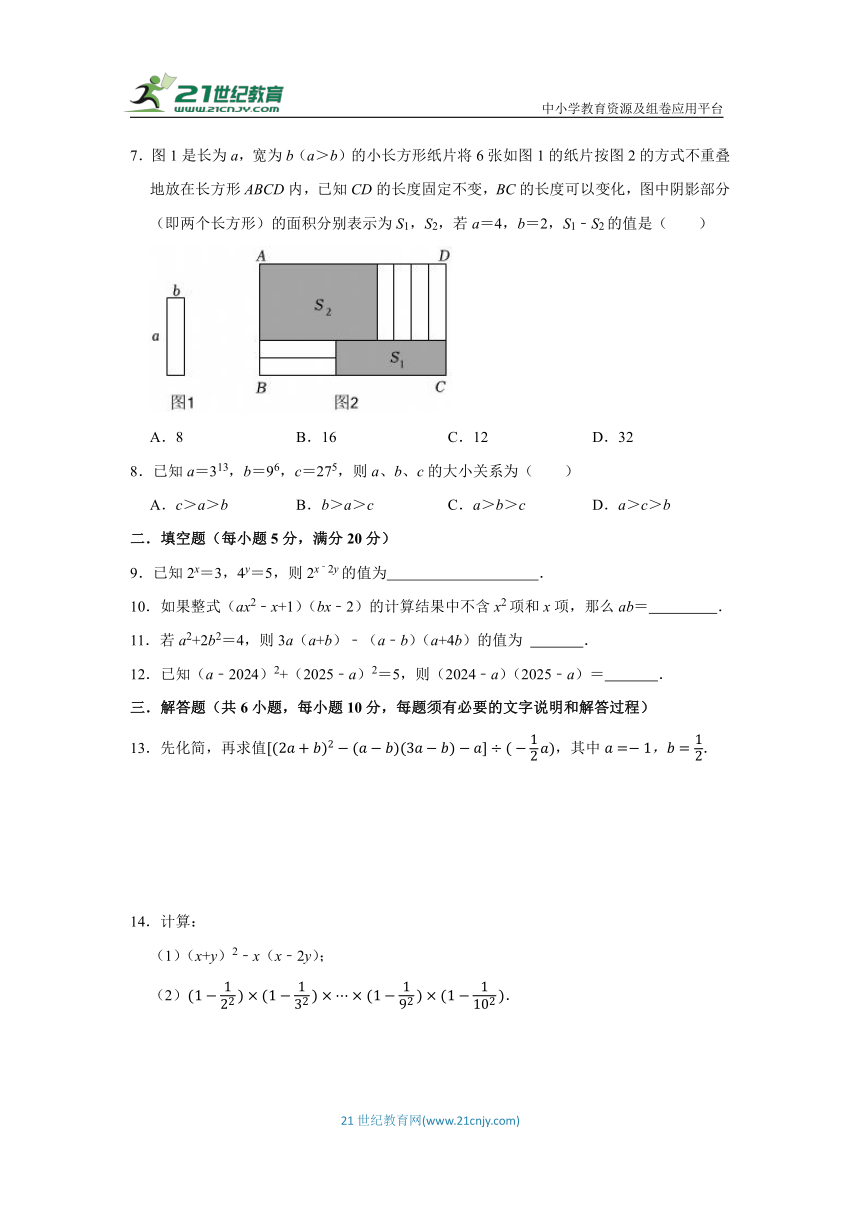
7．图1是长为a，宽为b（a＞b）的小长方形纸片将6张如图1的纸片按图2的方式不重叠地放在长方形ABCD内，已知CD的长度固定不变，BC的长度可以变化，图中阴影部分（即两个长方形）的面积分别表示为S1，S2，若a＝4，b＝2，S1﹣S2的值是（　　）
A．8 B．16 C．12 D．32
8．已知a＝313，b＝96，c＝275，则a、b、c的大小关系为（　　）
A．c＞a＞b B．b＞a＞c C．a＞b＞c D．a＞c＞b
二．填空题（每小题5分，满分20分）
9．已知2x＝3，4y＝5，则2x﹣2y的值为　 　．
10．如果整式（ax2﹣x+1）（bx﹣2）的计算结果中不含x2项和x项，那么ab＝　 　．
11．若a2+2b2＝4，则3a（a+b）﹣（a﹣b）（a+4b）的值为 　 　．
12．已知（a﹣2024）2+（2025﹣a）2＝5，则（2024﹣a）（2025﹣a）＝　 　．
三．解答题（共6小题，每小题10分，每题须有必要的文字说明和解答过程）
13．先化简，再求值，其中．
14．计算：
（1）（x+y）2﹣x（x﹣2y）；
（2）．
15．如图，正方形ABCD边长为a，正方形ECGF的边长为b，BC与CG在同一直线上，连接AG，EG．
（1）用含a，b的代数式表示图中阴影部分的面积；
（2）若a+b＝7，ab＝11，求出阴影部分的面积的值．
16．小亮学习多项式研究了多项式值为0的问题，发现当mx+n＝0或px+q＝0时，多项式A＝（mx+n）（px+q）＝mpx2+（mq+np）x+nq的值为0，把此时x的值称为多项式A的零点．
（1）已知多项式（3x﹣1）（x+2），则此多项式的零点为　 　；
（2）已知多项式B＝（x﹣2）（x+m）＝x2+（a﹣1）x﹣3a有一个零点为2，求多项式B的另一个零点；
（3）小亮继续研究（x﹣4）（x﹣2），x（x﹣6）及等，发现在x轴上表示这些多项式零点的两个点关于直线x＝3对称，他把这些多项式称为“3﹣系多项式”．若多项式M＝（2x﹣b）（cx﹣7c）＝ax2﹣（8a﹣4c）x+5b﹣4是“3﹣系多项式”，则a＝　 　，b＝　 　，c＝　 　．
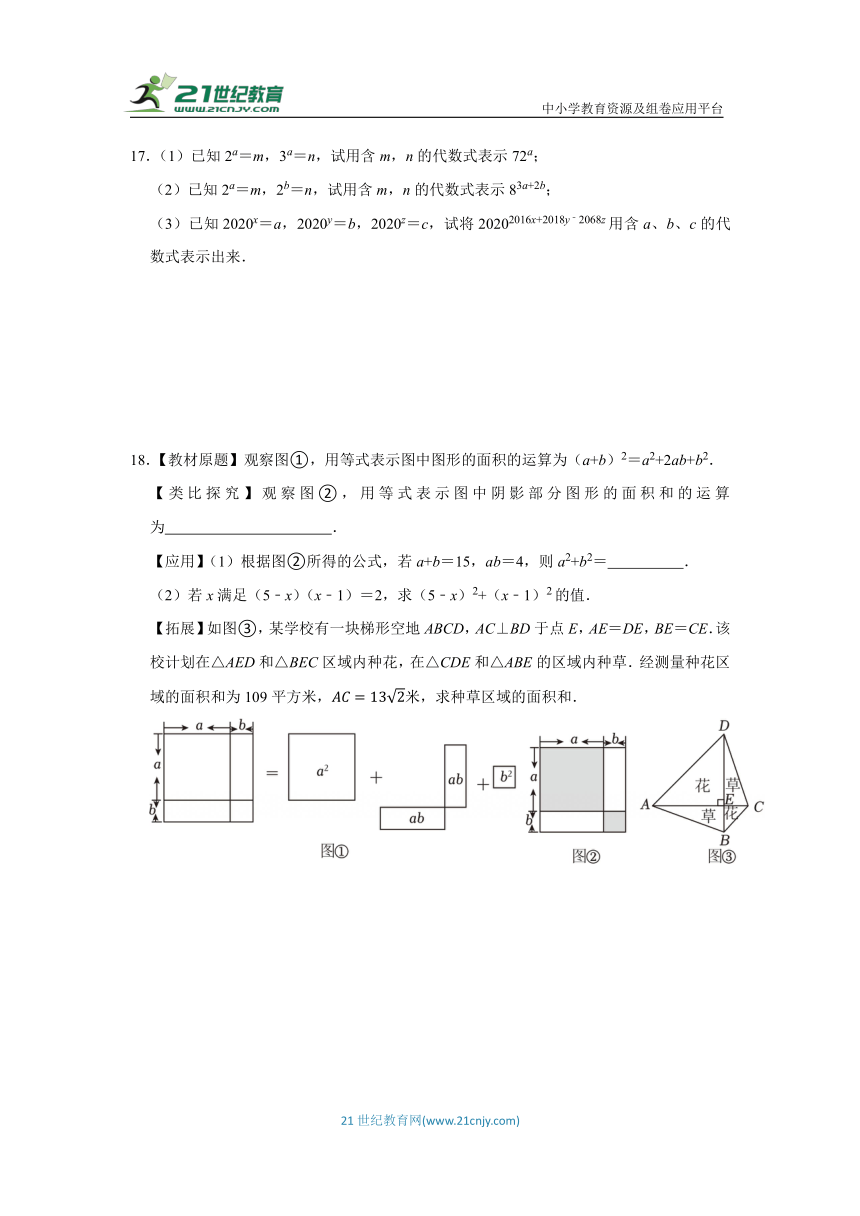
17．（1）已知2a＝m，3a＝n，试用含m，n的代数式表示72a；
（2）已知2a＝m，2b＝n，试用含m，n的代数式表示83a+2b；
（3）已知2020x＝a，2020y＝b，2020z＝c，试将20202016x+2018y﹣2068z用含a、b、c的代数式表示出来．
18．【教材原题】观察图①，用等式表示图中图形的面积的运算为（a+b）2＝a2+2ab+b2．
【类比探究】观察图②，用等式表示图中阴影部分图形的面积和的运算为　 　．
【应用】（1）根据图②所得的公式，若a+b＝15，ab＝4，则a2+b2＝　 　．
（2）若x满足（5﹣x）（x﹣1）＝2，求（5﹣x）2+（x﹣1）2的值．
【拓展】如图③，某学校有一块梯形空地ABCD，AC⊥BD于点E，AE＝DE，BE＝CE．该校计划在△AED和△BEC区域内种花，在△CDE和△ABE的区域内种草．经测量种花区域的面积和为109平方米，米，求种草区域的面积和．
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8
答案 B D B C C B B A
二、填空题
9．【解答】解：原式＝2x÷22y＝2x÷4y．
故答案为：．
10．【解答】解：∵多项式（ax2﹣x+1）（bx﹣2）＝abx3+（﹣2a﹣b）x2+（b+2）x﹣2不含x2项和x项，
∴﹣2a﹣b＝0且b+2＝0，
解得a＝1，b＝﹣2，
∴ab＝﹣2．
故答案为：﹣2．
11．【解答】解：3a（a+b）﹣（a﹣b）（a+4b）
＝3a2+3ab﹣（a2+4ab﹣ab﹣4b2）
＝3a2+3ab﹣a2﹣4ab+ab+4b2
＝2a2+4b2，
∵a2+2b2＝4，
∴2a2+4b2＝8，
则原式＝8，
故答案为：8．
12．【解答】解：设（2024﹣a）＝x，（2025﹣a）＝y，
∴x2+y2＝5，x﹣y＝2024﹣a﹣2025+a＝﹣1，
∴﹣2xy＝（x﹣y）2﹣（x2+y2）＝（﹣1）2﹣5＝﹣4，
∴xy＝2，
∴（2024﹣a）（2025﹣a）＝2，
故答案为：2．
三、解答题
13．【解答】解：
＝（4a2+4ab+b2﹣3a2+4ab﹣b2﹣a）÷（a）
＝（a2+8ab﹣a）÷（a）
＝﹣2a﹣16b+2，
当时，原式＝﹣2×（﹣1）﹣162
＝2﹣8+2
＝﹣4．
14．【解答】解：（1）（x+y）2﹣x（x﹣2y）
＝x2+2xy+y2﹣x2+2xy
＝4xy+y2；
（2）
．
15．【解答】解：（1）S阴影＝S正方形ABCD+S正方形CEFG﹣S△ABG﹣S△EFG
＝a2+b2a（a+b）b2
a2b2ab；
（2）∵a+b＝7，ab＝11，
∴）S阴影a2b2ab
（a2+b2﹣ab）
[（a+b）2﹣3ab]
（49﹣33）
16
＝8．
16．【解答】解：（1）令（3x﹣1）（x+2）＝0，
∴3x﹣1＝0或x+2＝0，
∴或x＝﹣2；
（2）把x＝2代入B，得B＝4+2（a﹣1）﹣3a＝0，
∴a＝2，
把a＝2代入B，得B＝x2+x﹣6＝（x﹣2）（x+3），
令x+3＝0，
∴x＝﹣3，
（3）∵M＝（2x﹣b）（cx﹣7c）＝0，
解得：或x＝7；
∴M的两个零点分别是或7，
根据“3﹣系多项式”的定义，有，
∴b＝﹣2，
把b＝﹣2代入M，
得M＝（2x﹣b）（cx﹣7c）
＝（2x+2）（cx﹣7c）
＝2cx2﹣12cx﹣14c
∵M＝ax2﹣（8a﹣4c）x+5b﹣4，
∴a＝2c，5b﹣4＝﹣14c，
∴c＝1，a＝2．
故答案为：2，﹣2，1．
17．【解答】解：（1）∵2a＝m，3a＝n，
∴原式＝（23×32）a
＝（2a）3 （3a）2
＝m3n2；
（2）∵2a＝m，2b＝n，
∴原式＝（23）3a﹣2b
＝29a+6b
＝（2a）9 （2b）6
＝m9n6；
（3）∵2020x＝a，2020y＝b，2020z＝c，
∴原式
．
18．【解答】解：【类比探究】观察图②，用等式表示图中阴影部分图形的面积和的运算为a2+b2＝（a+b）2﹣2ab，
故答案为：a2+b2＝（a+b）2﹣2ab；
（1）∵a+b＝15，ab＝4，a2+b2＝（a+b）2﹣2ab，
∴a2+b2＝152﹣2×4＝217，
故答案为：217；
（2）设m＝5﹣x，n＝x﹣1，则m+n＝4，mn＝（5﹣x）（x﹣1）＝2，
所以（5﹣x）2+（x﹣1）2
＝m2+n2
＝（m+n）2﹣2mn
＝16﹣4
＝12；
【拓展】设AE＝DE＝a，BE＝CE＝b，由题意得，a+b＝AE+CE＝AC＝13，S△AED+S△BECa2b2＝109，即a2+b2＝218，
S种草区域＝S△CDE+S△ABE
abab
＝ab
＝60，
即种草区域的面积和为60．
21世纪教育网(www.21cnjy.com)