3.4乘法公式培优练习（含答案）

中小学教育资源及组卷应用平台
3.4乘法公式培优练习浙教版2024—2025学年七年级下册
一、选择题
1．已知x2+y2＝13，xy＝﹣6，则x﹣y的值为（　　）
A．5 B．±5 C．1 D．±1
2．已知m﹣n＝3，则m2﹣n2﹣6n的值是（　　）
A．7 B．8 C．9 D．10
3．现有A，B两个正方形，将B放在A的内部如图甲所示；将A，B并列放置后构造新的正方形如图乙所示．若图甲和图乙中阴影部分的面积分别为6和17，则正方形A，B的面积之和为（　　）
A．11 B．9 C．21 D．23
4．我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图甲可以用来解释（a+b）2﹣（a﹣b）2＝4ab．那么通过图乙面积的计算，验证了一个恒等式，此等式是（　　）
A．a2﹣b2＝（a+b）（a﹣b）
B．（a﹣b）（a+2b）＝a2+ab﹣b2
C．（a﹣b）2＝a2﹣2ab+b2
D．（a+b）2＝a2+2ab+b2
5．已知（x﹣21）2+（x﹣25）2＝34，则（x﹣23）2的值是（　　）
A．10 B．13 C．26 D．34
二、填空题
6．若a＝2023×2024﹣1，b＝20232﹣2023×2024+20242，则a　 　b．（请用“＞”“＜”或“＝”表示）
7．某同学在计算4（5+1）（52+1）时，把4写成（5﹣1）后，发现可以连续运用平方差公式计算：4（5+1）（52+1）＝（5﹣1）（5+1）（52+1）＝（52﹣1）（52+1）＝252﹣1＝624．请借鉴该同学的经验，计算： 　 　．
8．若（2a+2b﹣1）（2a+2b+1）＝99，则a+b的值为 　 　．
9．如图，从边长为（a+5）的正方形纸片中剪去一个边长为（a+1）的正方形（a＞0），剩余部分沿虚线又剪拼成一个长方形（不重叠无缝隙），则这个长方形的周长为　 　．
10．若a+b＝8，ab＝15，a2+ab+b2的值为 　 　．
三、解答题
11．计算：
（1）（2x+3y）2﹣4（x+y）（x﹣y）；
（2）（x+y﹣6）（x﹣y+6）．
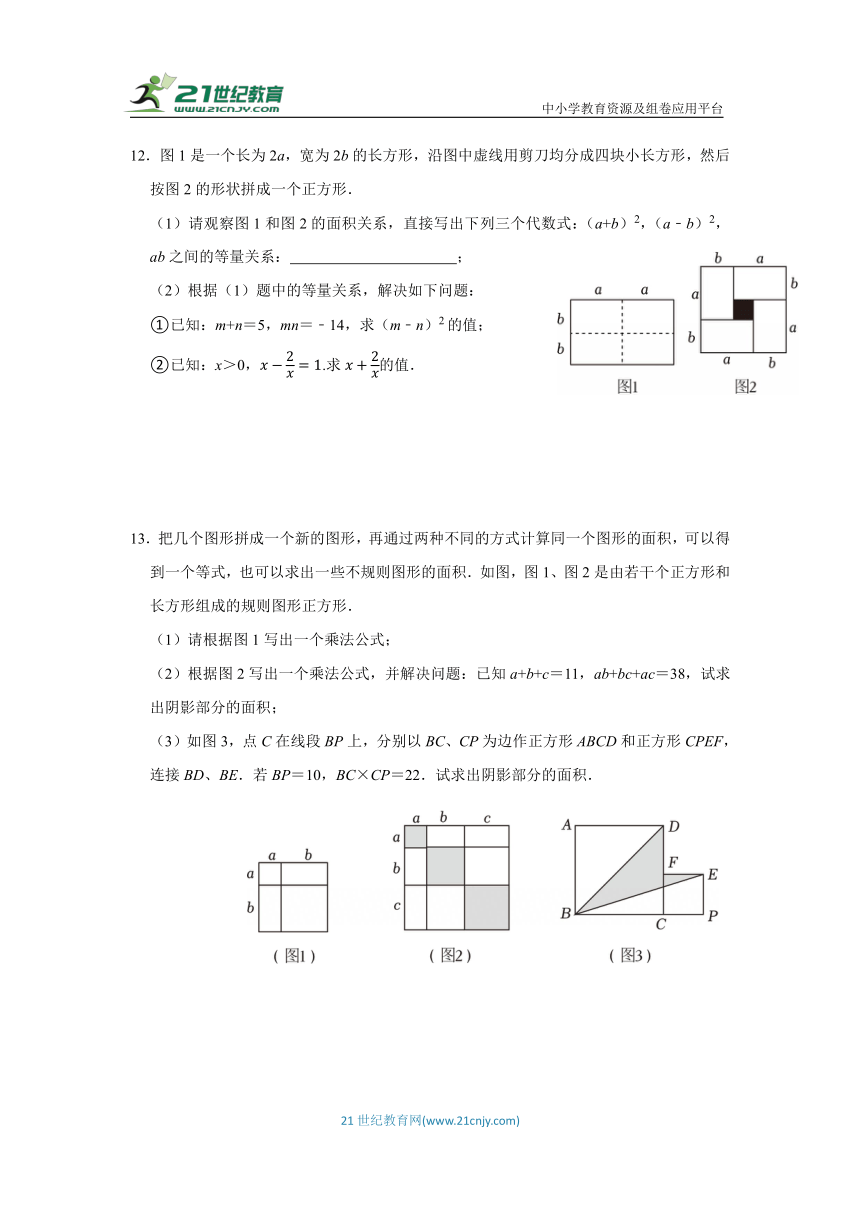
12．图1是一个长为2a，宽为2b的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
（1）请观察图1和图2的面积关系，直接写出下列三个代数式：（a+b）2，（a﹣b）2，ab之间的等量关系：　 　；
（2）根据（1）题中的等量关系，解决如下问题：
①已知：m+n＝5，mn＝﹣14，求（m﹣n）2的值；
②已知：x＞0，.求的值．
13．把几个图形拼成一个新的图形，再通过两种不同的方式计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．如图，图1、图2是由若干个正方形和长方形组成的规则图形正方形．
（1）请根据图1写出一个乘法公式；
（2）根据图2写出一个乘法公式，并解决问题：已知a+b+c＝11，ab+bc+ac＝38，试求出阴影部分的面积；
（3）如图3，点C在线段BP上，分别以BC、CP为边作正方形ABCD和正方形CPEF，连接BD、BE．若BP＝10，BC×CP＝22．试求出阴影部分的面积．
14．对于任意实数m，n，我们规定：F（m，n）＝m2+n2，H（m，n）＝mn，例如：F（1，2）＝12+22＝5，H（3，4）＝3×4＝12．
（1）填空：
①F（﹣1，3）＝　 　；
②若H（2，x）＝﹣6，则x＝　 　；
③若F（a，b）＝H（a，2b），则a﹣b　 　0．（填“＞”，“＜”或“＝”）；
（2）若x+2y＝5，且F（2x+3y，2x﹣3y）﹣H（7，x2+2y2）＝13，求xy与（x﹣2y）2的值．
15．如图1，将边长（a+b）的正方形剪出两个边长分别为a，b的正方形（阴影部分）和两个全等的长方形，观察图形，解答下列问题：
（1）用两种不同的方法表示图1阴影部分的面积，即用两个不同的代数式表示阴影部分的面积．方法1：　 　；方法2：　 　；从中你发现什么结论呢：　 　；
（2）根据上述结论，初步解决问题：已知a+b＝6，a2+b2＝20，求ab的值；
（3）解决问题：如图2，C是线段AB上一点，以AC，BC为边向两边作等腰直角三角形，记SRt△ACD＝S1，SRt△CBE＝S2，若AC+BC＝8，S1+S2＝25，求图中阴影部分的面积．
参考答案
一、选择题
题号 1 2 3 4 5
答案 B C D C B
二、填空题
6．【解答】解：∵a＝2023×2024﹣1，b＝20232﹣2023×2024+20242，
∴b﹣a＝20232﹣2023×2024+20242﹣2023×2024+1
＝20232﹣2×2023×2024+20242+1
＝（2023﹣2024）2+1
＝（﹣1）2+1
＝1+1
＝2＞0，
∴a＜b，
故答案为：＜．
7．【解答】解：
＝2
＝2，
故答案为：2．
8．【解答】解：∵（2a+2b﹣1）（2a+2b+1）＝99，
∴[（2a+2b）﹣1）][（2a+2b）+1]＝99，
∴（2a+2b）2﹣1＝99，
∴（2a+2b）2＝100，
∴2a+2b＝±10，
∴a+b＝5或﹣5．
故答案为：5或﹣5．
9．【解答】解：拼成的长方形的长为a+5+a+1＝2a+6，宽为a+5﹣（a+1）＝4，
所以周长为（2a+6+4）×2＝4a+20，
故答案为：4a+20．
10．【解答】解：∵a+b＝8，ab＝15，
∴a2+ab+b2
＝（a+b）2﹣ab
＝82﹣15
＝64﹣15
＝49，
故答案为：49．
三、解答题
11．【解答】解：（1）原式＝（4x2+12xy+9y2）﹣（4x2﹣4y2）
＝4x2+12xy+9y2﹣4x2+4y2
＝12xy+13y2．
（2）原式＝x2﹣（y﹣6）2
＝x2﹣y2+12y﹣36．
12．【解答】解：（1）图2，大正方形的边长为a+b，因此面积为（a+b）2，中间小正方形的边长为a﹣b，因此面积为（a﹣b）2，4个空白长方形的面积和为4ab，
所以有（a+b）2＝（a﹣b）2+4ab，
故答案为：（a+b）2＝（a﹣b）2+4ab；
（2）①（m﹣n）2＝（m+n）2﹣4mn＝25+56＝81；
②∵（x）2＝（x）2+8＝1+8＝9，而x＞0，
∴x3．
13．【解答】解：（1）图1整体上是边长为a+b的正方形，因此面积为（a+b）2，拼成图1的四个部分的面积和为a2+2ab+b2，
所以有（a+b）2＝a2+2ab+b2；
（2）图2整体上是边长为a+b+c的正方形，因此面积为（a+b+c）2，拼成图1的九个部分的面积和为a2+b2+c2+2ab+2bc+2ac，
所以有（a+b+c）2＝a2+b2+c2+2（ab+bc+ac），
∵a+b+c＝11，ab+bc+ac＝38，
∴112＝a2+b2+c2+2×38，
∴a2+b2+c2＝45，
答：阴影部分的面积为45；
（3）设 BC＝a，CP＝b，
∴S阴影＝S正方形ABCD+S正方形CPEF﹣S△ABD﹣S△BPE
＝a2+b2a2b（a+b）
[（a+b）2﹣3ab]；
∵BP＝10，BC×CP＝22，即a+b＝10，ab＝22，
∴S阴影（100﹣66）＝17，
答：阴影部分的面积为17．
14．【解答】解：（1）①F（﹣1，3）＝（﹣1）2+32＝10；
②若H（2，x）＝﹣6，
则2x＝﹣6，
则x＝﹣3；
③若F（a，b）＝H（a，2b），
则a2+b2＝2ab，
则（a﹣b）2＝0，
则a﹣b＝0，
故答案为：①10；②﹣3；③＝；
（2）∵F（2x+3y，2x﹣3y）﹣H（7，x2+2y2）＝13，
∴（2x+3y）2+（2x﹣3y）2﹣7（x2+2y2）＝13，
即x2+4y2＝13，
∵x+2y＝5，
∴x2+4y2+4xy＝25，
∴xy＝3，
∴（x﹣2y）2＝x2+4y2﹣4xy＝1．
15．【解答】解：（1）方法1：根据题意可知，阴影部分面积为边长为a和边长为b的正方形面积之和，
∴；
方法2：根据题意可知，阴影部分面积为边长为（a+b）的正方形面积减去长为a，宽为b的长方形面积×2，
∴，
根据阴影部分面积相等可知：a2+b2＝（a+b）2﹣2ab．
故答案为：a2+b2；（a+b）2﹣2ab；a2+b2＝（a+b）2﹣2ab；
（2）∵a+b＝6，a2+b2＝20，
由（1）得：a2+b2＝（a+b）2﹣2ab，
∴；
（3）设AC＝x，BC＝y，
∵AC+BC＝8，S1+S2＝25，
∴，
∴，
∴阴影部分的面积为．
21世纪教育网(www.21cnjy.com)