1.1直线的相交同步练习（含解析）

中小学教育资源及组卷应用平台
1.1直线的相交
学校:___________姓名：___________班级：___________考号：___________
一、单选题
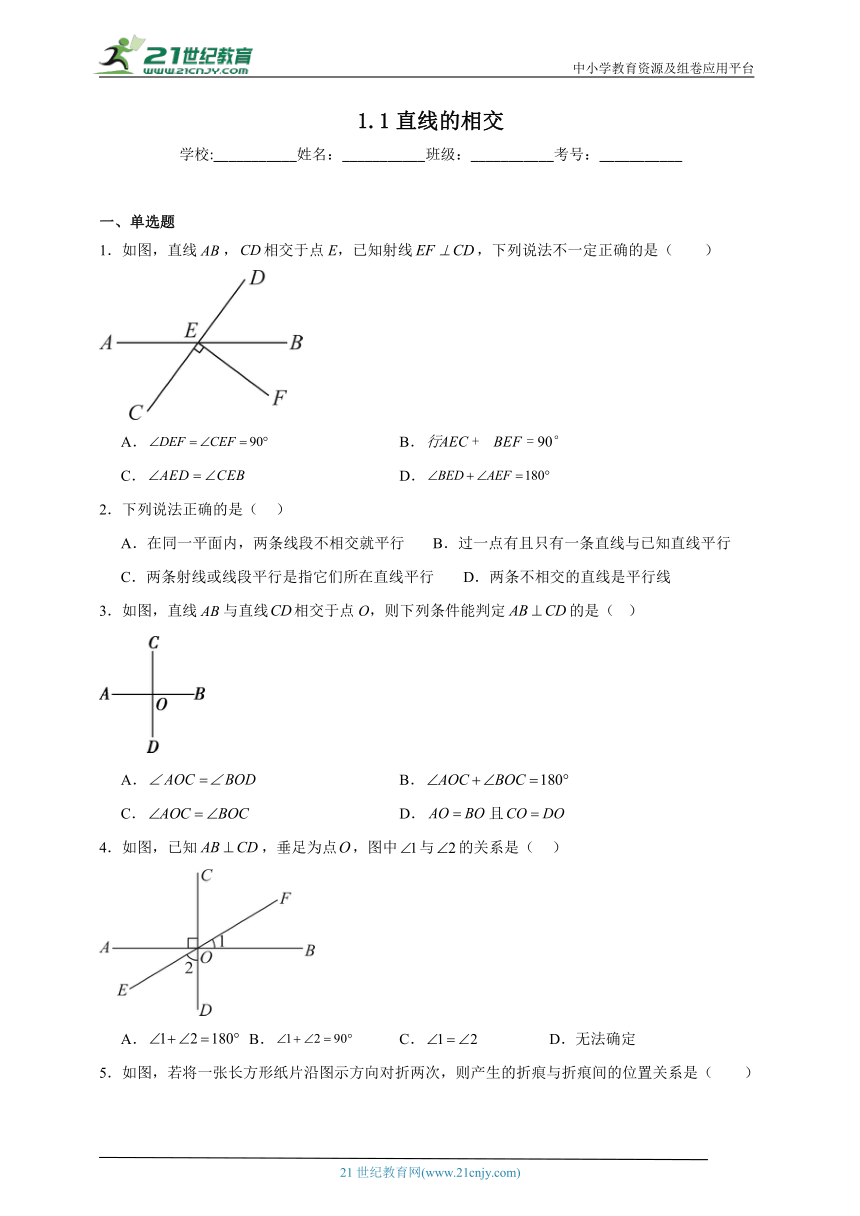
1．如图，直线，相交于点E，已知射线，下列说法不一定正确的是（　　）
A． B．
C． D．
2．下列说法正确的是（ ）
A．在同一平面内，两条线段不相交就平行 B．过一点有且只有一条直线与已知直线平行
C．两条射线或线段平行是指它们所在直线平行 D．两条不相交的直线是平行线
3．如图，直线与直线相交于点O，则下列条件能判定的是（ ）
A． B．
C． D．且
4．如图，已知，垂足为点，图中与的关系是（ ）
A． B． C． D．无法确定
5．如图，若将一张长方形纸片沿图示方向对折两次，则产生的折痕与折痕间的位置关系是（　　）
A．平行 B．垂直 C．平行或垂直 D．相交但不垂直
6．下列图形中和互为对顶角的是（ ）
A． B． C． D．
7．如图,直线∥，于E，交 于F，直线交于M，于N，于O，则直线和之间的距离是哪个线段的长（ ）
A． B． C． D．
8．小宁同学在体育课上进行跳远测试，体育老师在测量他的跳远成绩时，用到数学基本原理，最恰当的是两点之间（ ）
A．线段最短 B．垂线段最短
C．在同一平面内，过一点有且只有一条直线与已知直线垂直 D．经过直线外一点，有且只有一条直线与这条直线平行
9．如图，，且，则的度数是（　　）
A． B． C． D．
10．下面四个图形中，∠1与∠2是对顶角的是（　　）
A． B． C． D．
11．已知 与 是对顶角，且，则 的度数为（ ）
A． B． C． D．
12．下列说法正确的有（ ）
①不相交的两条直线是平行线；
②在同一平面内，两条不相交的线段是平行线；
③两条射线或线段平行，是指它们所在的直线平行；
④不相交的两条射线一定平行．
A．0个 B．1个 C．2个 D．3个
二、填空题
13．如图，为直线上一点，将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的上方．将三角板绕点以每秒3°的速度沿逆时针方向旋转一周．则经过 秒后，．
14．如图，三条直线相交于同一点．如果，那么的度数为 ．
15．在体育课上某同学跳远的情况如图所示，直线l表示起跳线，经测量，PB＝3.3米，PC＝3米，PD＝3.5米，则该同学的实际立定跳远成绩是 米．
16．已知直线相交于点O，平分，且，射线，则 ．
17．如图直线AB，CD相交于O，直线FE⊥AB于O，∠BOD＝75°，则∠COF的度数为 度．
三、解答题
18．如图，一辆汽车在直线形公路上由A向B行驶，点C，D分别是位于公路两侧的村庄，设汽车行驶到点E时，离村庄C最近，行驶到点F时，离村庄D最近．
(1)请你在上分别画出E，F两点的位置；
(2)如果在公路上有一个点P到村庄C和村庄D的距离之和最短，请在公路上画出点P．
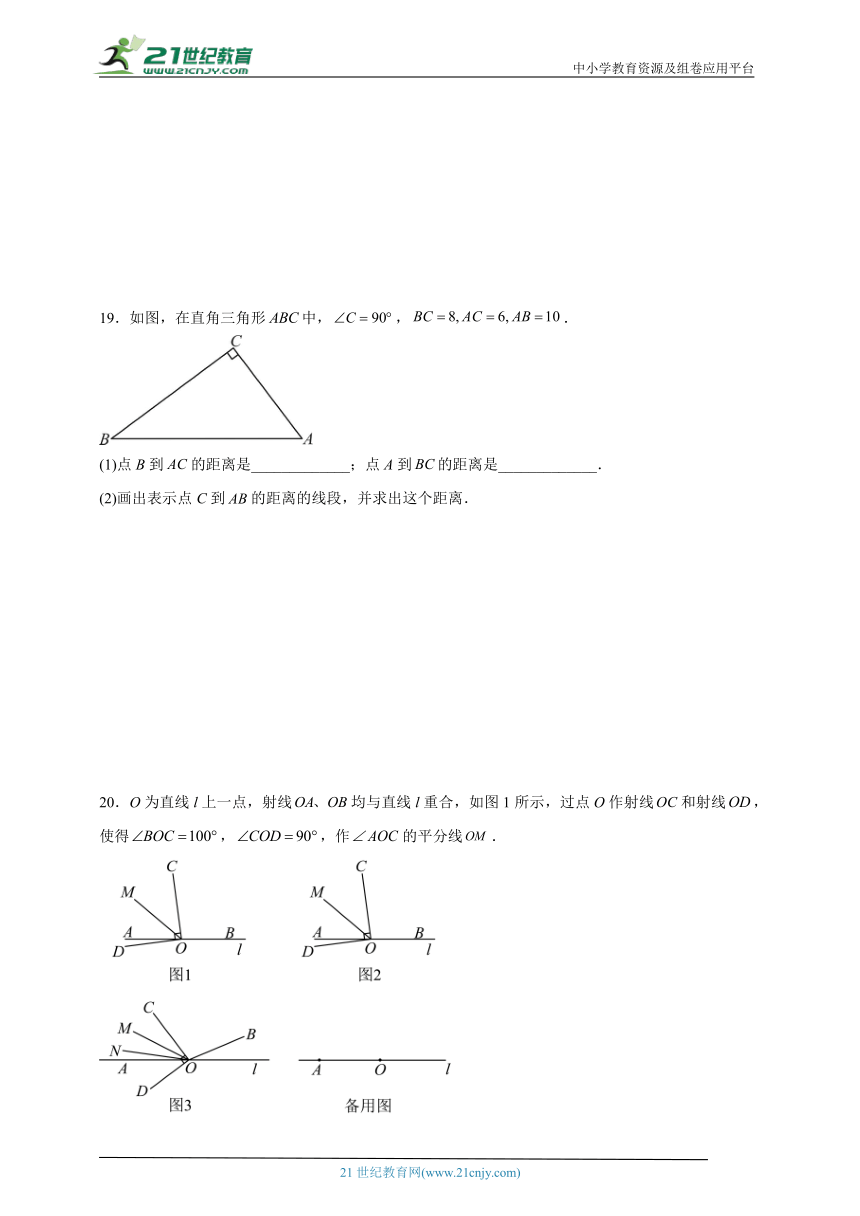
19．如图，在直角三角形中，，．
(1)点B到的距离是_____________；点A到的距离是_____________．
(2)画出表示点C到的距离的线段，并求出这个距离．
20．O为直线l上一点，射线均与直线l重合，如图1所示，过点O作射线和射线，使得，，作的平分线．
(1)求与的度数；
(2)作射线，使得，请在图2中画出图形，并求出的度数；
(3)如图3，将射线从图1位置开始，绕点O以每秒的速度逆时针旋转一周，作的平分线，当时，求旋转的时间．
21．如图，①过点Q作QD⊥AB，垂足为点D；
②过点P作PE⊥AB，垂足为点E；
③过点Q作QF⊥AC，垂足为点F；
④连P，Q两点；
⑤P，Q两点间的距离是线段______的长度；
⑥点Q到直线AB的距离是线段______的长度；
⑦点Q到直线AC的距离是线段______的长度；
⑧点P到直线AB的距离是线段______的长度．
22．如图，直线与交于点O，，直线经过点O，平分，、求，，的度数．
23．按下列要求画图并填空：如图，直线AB与CD相交于点O，P是CD上的一点．
(1)过点P画出CD的垂线，交直线AB于点E；
(2)过点P画PF⊥AB，垂足为点F；
(3)点O到直线PE的距离是线段　　的长；
(4)点P到直线CD的距离为　　．
24．如图，P是∠AOB的边OB上一点．
(1)过点P画OA的垂线，垂足为H；
(2)过点P画OB的垂线，交OA于点C；
(3)点O到直线PC的距离是线段________的长度；
(4)比较PH与PC的大小，并说明理由．
《1.1直线的相交》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C B A C B B B C
题号 11 12
答案 C B
1．D
【分析】本题考查垂线概念，对顶角性质，熟练掌握垂线概念与对顶角性质是解题的关键．
根据垂线概念与对顶角性质逐项判定即可．
【详解】解：A、因为，所以，故此选项正确不符合题意；
B、因为，所以，故此选项正确不符合题意；
C、由题图可得和为对顶角，所以，故此选项正确不符合题意；；
D、因为，而无法确定与相等，所以不一定正确，故此选项不一定正确，符合题意．
故选：D．
2．C
【分析】根据平面内两条直线的位置关系分别判断．
【详解】解：A、在同一平面内，两条线段不相交，也不一定平行，故错误，不合题意；
B、过直线外一点有且只有一条直线与已知直线平行，故错误，不合题意；
C、两条射线或线段平行是指它们所在的直线平行，故正确，符合题意；
D、平面内，两条不相交的直线是平行线，故错误，不合题意；
故选：C．
【点睛】本题考查了平面内两条直线的位置关系，解题的关键是掌握平行线的定义．
3．C
【分析】本题主要考查了垂线，对顶角，解答本题的关键是通过条件计算出其中一个角为．根据垂直定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直进行判定即可．
【详解】解：A、是对顶角，对顶角相等，不能判定垂直，故此选项不符合题意；
B、和是邻补角，邻补角的和是，所以不能得到，不能判定垂直，故此选项不符合题意；
C、和是邻补角，邻补角的和是，而，则，可以判定两直线垂直，故此选项符合题意；
D、且无法判定两直线垂直，故此选项不符合题意；
故选：C．
4．B
【分析】根据垂线的定义得出，然后由平角的定义即可得出与的关系．
【详解】解：，
，
，
，
故选：B．
【点睛】本题考查了垂线的定义，平角的定义，熟练掌握知识点是解题的关键．
5．A
【分析】本题考查平行线的知识，解题的关键是掌握平行线的性质，即可．
【详解】∵长方形对折两次，产生的折痕与折痕间的位置如下：

∴产生的折痕与折痕间的位置关系是平行，
故先：A．
6．C
【分析】根据对顶角的定义来判断，两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做对顶角．
【详解】解：根据对顶角的定义可知，只有C中属于对顶角，
故选C．
【点睛】本题主要考查了对顶角的识别，熟知对顶角的定义是解题的关键．
7．B
【分析】根据夹在两条平行线间的垂线段的长度即为两平行线的距离，即可判断．
【详解】因为直线∥，于E，交于F，
所以直线EF也垂直于直线CD，
则直线AB和CD之间的距离是线段EF的长．
故选B．
8．B
【分析】根据垂线段的性质解答即可，垂线段的性质：垂线段最短．
【详解】解：体育课上老师测量同学的跳远成绩，这里面蕴含的数学原理是垂线段最短．
故选：B．
【点睛】本题考查了垂线段的性质，垂线段：从直线外一点引一条直线的垂线，这点和垂足之间的线段叫做垂线段．垂线段的性质：垂线段最短．正确理解此性质，垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．
9．B
【分析】根据垂直的定义，由，得．由，根据角的和差关系得到．
【详解】解：∵，
∴．
∵，
∴．
故选：B．
【点睛】本题考查了垂线，余角的知识．要注意领会由垂直得直角这一要点．
10．C
【分析】一个角的两边是另一个角的两边的反向延长线，据此判断，A不是；B不是；C是的；D不是．
【详解】A、∠1与∠2不是对顶角，故此选项不符合题意；
B、∠1与∠2不是对顶角，故此选项不符合题意；
C、∠1与∠2是对顶角，故此选项符合题意；
D、∠1与∠2不是对顶角，故此选项不符合题意；
故选：C．
【点睛】本题考查了对顶角，解决此题的关键是熟练运用对顶角的定义判断.
11．C
【分析】根据对顶角相等，即，结合已知，即可求的度数．
【详解】解：∵ 与 是对顶角
∴，
∵，
∴，
故选：C．
【点睛】本题考查了对顶角相等，熟练掌握对顶角相等是解题的关键．
12．B
【分析】本题考查了平行线的认识，射线、线段、直线的认识，据此相关性质内容进行逐项分析，即可作答．
【详解】解：在同一平面内，不相交的两条直线是平行线，故①②是错误的；
两条射线或线段平行，是指它们所在的直线平行，故③是正确的；
不相交的两条射线不一定平行，故④是错误的；
故选：B．
13．10或70/70或10
【分析】分两种情况讨论，利用旋转的性质即可求解．
【详解】解：如图，，
∵，，
∴，，
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转，
∴(秒)；
如图，，
∵，，
∴，，
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转，
∴旋转角为，
∴(秒)；
故答案为：10或70．
【点睛】本题考查了垂直的定义、角的和差等知识，解题的关键是理解题意，画出图形，利用垂直的定义求解即可．
14．/90度
【分析】此题主要考查了对顶角，平角，关键是掌握对顶角相等，平角．首先设，则，进而得到方程，再解方程可得的值，即可算出，再根据对顶角相等可得答案．
【详解】解：设，则，
∴，
解得：，
∴，
∴，
故答案为：．
15．3
【分析】因为垂线段最短，所以点P到起跳线l的垂线段的长度即PC的长度就是立定跳远的成绩．
【详解】∵PC⊥BD，PC＝3米，
∴该同学的实际立定跳远成绩是3米．
故答案为：3．
【点睛】此题考查了点到直线的距离，解题的关键是知道立定跳远的成绩即为起跳线外一点到这条起跳线的垂线段的长度，即要知道直线外一点与直线上各点连接的所有线段中，垂线段最短．
16．或
【分析】分两种情况，由角平分线定义求出，由对顶角的性质得到，由垂直的定义得到，即可求出的度数．
【详解】解：如图①，
平分，，
，
，
射线，
，
；

如图②，
平分，，
，
，
射线，
，
，
或．
故答案为：或．
【点睛】本题考查垂线的意义，角平分线的定义，对顶角的性质，关键是画出图形，分两种情况讨论．
17．15
【分析】利用图中角与角的关系即可求得，即∠COF＝∠DOE＝90°﹣∠BOD．
【详解】解：∵直线FE⊥AB于O，
∴∠BOE＝90°，
∵∠DOE＝∠BOE﹣∠BOD，∠BOD＝75°，
∴∠DOE＝15°，
∴∠COF＝∠DOE＝15°．
故答案为：15．
【点睛】此题考查的知识点是垂线、角的计算及对顶角知识，关键是根据垂线、垂线定义得出所求角与已知角的关系转化求解．
18．(1)见解析
(2)见解析
【分析】本题考查了垂线段最短；两点之间，线段最短；
（1）根据垂线段最短，分别过点C、D向直线作垂线即可；
（2）根据两点之间，线段最短，连接与直线的交点即为点P．
【详解】（1）解：点E，F的位置如图所示：
（2）点P的位置如图所示．
19．(1)8； 6
(2)图见解析；点C到的距离是
【分析】本题考查了点到直线的距离，熟练掌握点到直线的距离的概念及等面积法是解题的关键，
（1）根据点到直线的距离的概念进行求解即可得到答案；
（2）过点作，则线段表示点C到的距离，再利用等面积法即可求得线段的长．
【详解】（1）解：∵三角形为直角三角形，，，
∵，
∴点B到的距离是的长度为8，
∵
∴点A到的距离是的长度为6．
故答案为：8；6．
（2）解：过点作，如图，线段即为所求．
，即，
，
∴点C到的距离是．
20．(1)，
(2)或
(3)6秒或秒
【分析】（1）根据，，即可得出的度数，根据角平分线的定义得出，然后根据得出的度数；
（2）根据题意得出的度数，然后分两种情况进行讨论：①当射线在内部时；②当射线在外部时；分别进行计算即可；
（3）根据平分得出，根据题意画出图形，计算的角度，然后计算时间即可．
【详解】（1）解：由题意可知，，
∵，
∴，
∵平分，
∴，
∴；
（2）由（1）知，，
∴，
①当射线在内部时，如图2（1），
；
②当射线在外部时，如图2（2），
，
综上所述，的度数为或；
（3）∵平分，
∴，
①如图3，
，
∵平分，
∴，
∴，
∴旋转的时间（秒）；
②如图3（1），
此时，，
∵平分，
∴，
∴，
∴，
∴旋转的时间（秒）；
综上所述，旋转的时间为6秒或秒．
【点睛】本题主要考查角度的计算，角平分线的定义等内容；第（2）问进行合适的分类讨论是解题的关键；第（3）问，搞清楚在射线旋转的过程中，和的相对位置在不断的变化，以此进行分类画图．
21．①②③④作图见解析；⑤PQ；⑥QD；⑦QF；⑧PE
【分析】由题意①②③④根据题目要求即可作出图示，⑤⑥⑦⑧根据两点之间距离及点到直线的距离的定义即可得出答案．
【详解】①②③④作图如图所示；
⑤根据两点之间距离即可得出P，Q两点间的距离是线段PQ的长度；
⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度；
⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度；
⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度.
【点睛】本题主要考查基本作图和两点之间距离及点到直线的距离，熟练掌握相关概念与作图方法是解题的关键．
22．，，
【分析】题主要考查了角平分线的定义，对顶角的性质等知识，熟练运用角的和差关系进行计算是解题的关键．
根据对顶角相等，得，再根据，则，再利用角平分线的定义得出的度数，然后由，可求得的度数．
【详解】解：根据对顶角相等，得．
，
，
平分，
，
，
，，．
23．(1)见解析
(2)见解析
(3)OP
(4)0
【分析】（1）根据垂线的定义，利用三角板的两条直角边画图即可；
（2）根据垂线的定义，利用三角板的两条直角边画图即可；
（3）根据直线外一点到这条直线的垂线段的长度是这点到直线的距离解答即可；
（3）根据直线上的点到这条直线的距离等于0解答即可．
【详解】（1）解：如图，直线PE即为所求；
（2）解：如图，直线PF即为所求；
（3）解：点O到直线PE的距离是线段OP的长．
故答案为：OP；
（4）解：由图可知，点P到直线CD的距离为0，
故答案为：0．
【点睛】本题考查了垂线的作法，点到直线的距离等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
24．(1)见解析
(2)见解析
(3)OP
(4)PH【分析】（1）根据垂线的画法，画出图形，即可求解；
（2）根据垂线的画法，画出图形，即可求解；
（3）根据线段OP的长是点C到直线OB的距离，即可求解；
（4）根据直线外一点到直线上各点连接的所有线中，垂线段最短，即可求解．
【详解】（1）解：如图，直线PH即为所求；
（2）解：如图，直线PC即为所求；
（3）解：点O到直线PC的距离是线段OP的长度；
故答案为：OP
（4）解：PH∵点到直线，垂线段最短，
∴PH【点睛】本题主要考查了画垂线，点到直线的距离，熟练掌握点到直线，垂线段最短是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)