1.3平行线同步练习（含解析）

中小学教育资源及组卷应用平台
1.3平行线
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，点P是直线AB外一点，过点P分别作，，则点C、P、D三个点必在同一条直线上，其依据是（　　）
A．两点确定一条直线
B．同位角相等，两直线平行
C．过直线外一点有且只有一条直线与这条直线平行
D．平行于同一条直线的两条直线平行
2．在同一平面内有a，b，c三条直线，若，且a与c相交，那么b与c的位置关系是（　　）
A．平行 B．相交
C．平行或相交 D．不能确定
3．下列说法中，正确的个数有（ ）
（1）若，，则；（2）过一点有且只有一条直线与已知直线平行；（3）两条直线不相交就平行；（4）两点之间，直线最短．
A．1个 B．2个 C．3个 D．4个
4．下列说法正确的有（ ）
①同位角相等；②过一点有且只有一条直线与已知直线垂直；③若，，则；④任何一个数都有平方根和立方根
A．个 B．个 C．个 D．个
5．给出下列说法：（1）过平面内一点有且只有一条直线与已知直线平行；（2）相等的两个角是对顶角；（3）从直线外一点到这条直线的垂线段，叫做这点到直线的距离；（4）不相交的两条直线叫做平行线；（5）垂直于同一条直线的两条直线平行．其中正确的有（ ）
A．0个 B．1个 C．2个 D．3个
6．小明与小刚在讨论数学问题时，有如下对话：
小明：在同一平面内，过一点A有且只有一条直线与已知直线m平行．
小刚：在同一平面内，过一点A有且只有一条直线与已知直线m垂直．
对于两个人的说法，正确的是（ ）
A．小明对 B．小刚对 C．两人均对 D．两人均不对
7．下列说法中不正确的有（ ）
①过任意一点可作已知直线的一条平行线
②同一平面内两条不相交的直线是平行线
③过已知直线外一点只能画一条直线与已知直线平行
④平行于同一直线的两直线平行．
A．0个 B．1个 C．2个 D．3个
8． 下列说法错误的是（　　）
A．对顶角相等 B．两点之间所有连线中，线段最短
C．等角的补角相等 D．过任意一点P，都能画一条直线与已知直线平行
9．如图，若，则与的位置关系是（ ）
A．平行 B．延长后才平行 C．垂直 D．无法确定
10．下面不能检验直线与平面垂直的工具是（　　）
A．铅垂线 B．三角尺 C．长方形纸片 D．合页型折纸
11．下列说法错误的是（ ）
A．对顶角相等
B．同角（等角）的余角相等
C．过一点有且只有一条直线与已知直线平行
D．过一点有且只有一条直线与已知直线垂直
12．已知是平面内任意一点，过点画一条直线与的边平行，则这样的直线（ ）
A．有一条 B．有两条 C．不存在 D．以上情况都有可能
二、填空题
13．如图，，，则点在同一直线上，理由是 ．
14．如图，过三角形的边的中点画平行于的直线，这样的直线能画 条．
15．如果两条直线都与第三条直线平行，那么这两条直线互相 ．
几何语言表示：
∵a∥c ， c∥b（已知）
∴ ∥ （如果两条直线都和第三条直线平行，那么这两条直线也互相平行）
16．三条直线，则 ，理由是 ．
17．下列说法中：
①过直线外一点有且只有一条直线与已知直线平行；
②已知直线a，b，c，若，则，
③相等的角是对顶角；
④直线外一点与直线上各点连接的所有线段中，垂线段最短．
其中正确的有 ．（填序号）
三、解答题
18．在如图所示的方格纸中，每个小正方形的顶点称为格点，每个小正方形的边长为1，已知四边形ABCD的四个顶点在格点上，利用格点和直尺按下列要求画图：
(1)过点C画AD的平行线CE；
(2)过点B画CD的垂线，垂足为F．
(3)线段CF表示点 到线段 的距离．
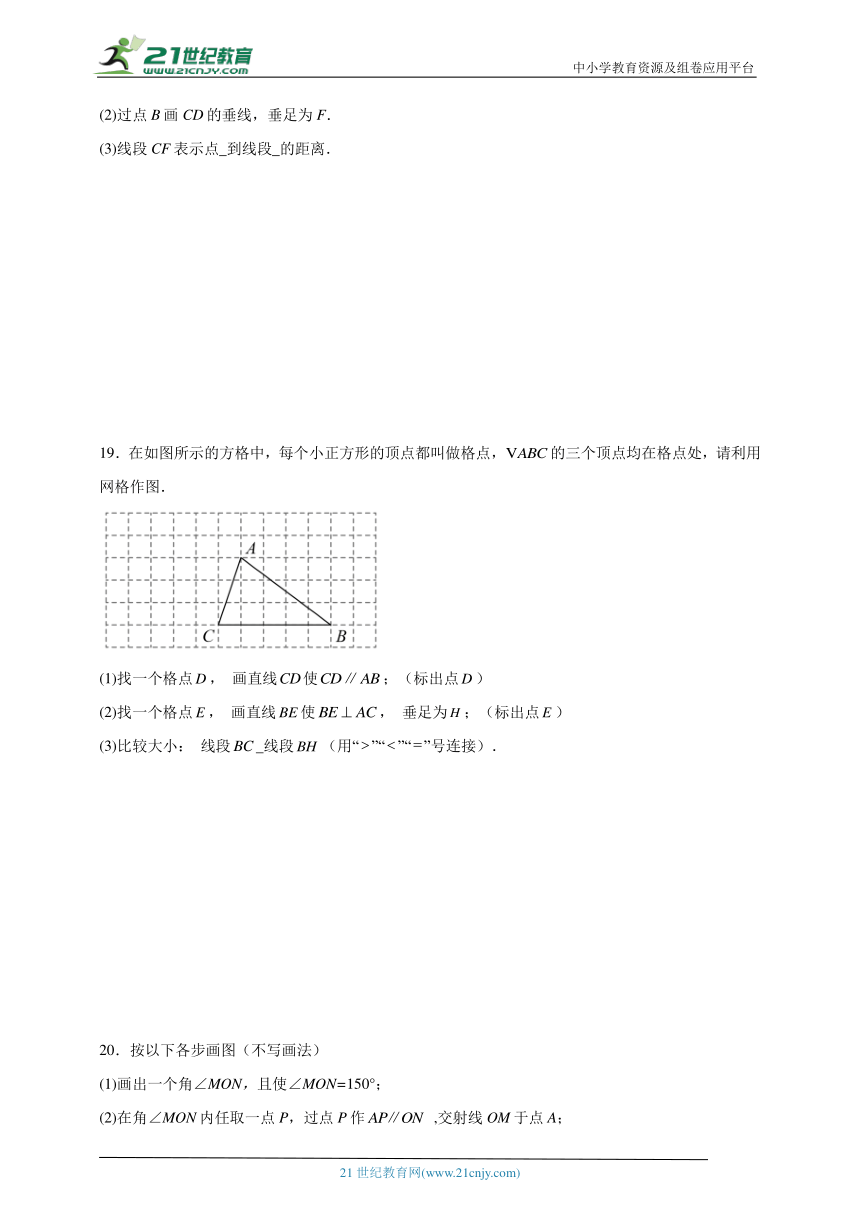
19．在如图所示的方格中，每个小正方形的顶点都叫做格点，的三个顶点均在格点处，请利用网格作图．
(1)找一个格点， 画直线使；（标出点）
(2)找一个格点， 画直线使， 垂足为；（标出点）
(3)比较大小： 线段 线段（用“”“”“”号连接）．
20．按以下各步画图（不写画法）
(1)画出一个角∠MON，且使∠MON=150°；
(2)在角∠MON内任取一点P，过点P作 ,交射线OM于点A；
(3)过点A作垂线AB，使AB⊥ON,垂足为点B；
(4)画射线PO(或反向延长射线PO)交垂线AB于点C
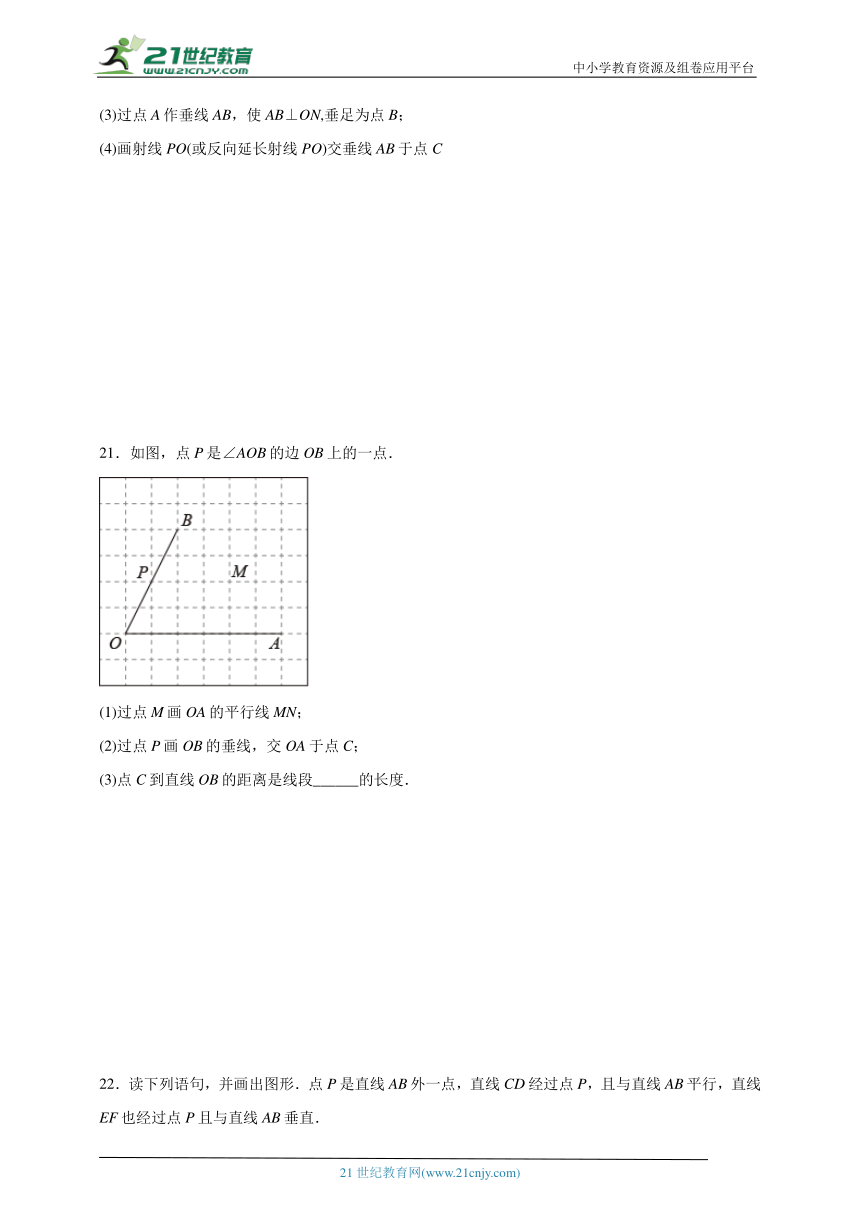
21．如图，点P是∠AOB的边OB上的一点．
(1)过点M画OA的平行线MN；
(2)过点P画OB的垂线，交OA于点C；
(3)点C到直线OB的距离是线段______的长度．
22．读下列语句，并画出图形．点P是直线AB外一点，直线CD经过点P，且与直线AB平行，直线EF也经过点P且与直线AB垂直．
23．如图，平面内有两条直线，点A在直线上，按要求画图并填空：
(1)过点A画直线的垂线，垂足为点B，点A到直线距离为线段______的长度；
(2)过点A画直线交直线于点于点C；
(3)过点A画直线；
24．如图，按要求作图并解答问题．
(1)过上一点D作的平行线，交于点；
(2)过点C作；
(3)直线的位置关系是什么？请说明理由．
《1.3平行线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B A A B B D A C
题号 11 12
答案 C D
1．C
【分析】根据过直线外一点有且只有一条直线与这条直线平行即可．
【详解】解：因为，
∴．
所以则点C、P、D三个点必在同一条直线上，理由：过直线外一点有且只有一条直线与这条直线平行
故选：C．
【点睛】本题考查过直线外一点有且只有一条直线与这条直线平行，熟练掌握性质定理解答此题的关键．
2．B
【分析】本题主要考查了平行线与相交线，根据平行于同一条直线的两条直线平行，进行判断即可．
【详解】解：若，且a与c相交，
∴b与c相交，
故选：B．
3．B
【分析】根据平行线的性质与判定，平行线公理，两直线的位置关系，两点之间线段最短，逐项分析判断即可求解．
【详解】（1）若，，则；故（1）正确，符合题意；
（2）过直线外一点有且只有一条直线与已知直线平行，故（2）不正确，不符合题意；
（3）两条直线不相交就平行，故（3）正确，符合题意；
（4）两点之间，线段最短．故（4）不正确，不符合题意；
故选：B．
【点睛】本题考查了平行线的性质与判定，平行线公理，两直线的位置关系，两点之间线段最短，熟练掌握以上知识是解题的关键．
4．A
【分析】根据同位角，两直线的位置关系，平行公理及其推论，平方根和立方根的概念判断各项即可．
【详解】解：①同位角不一定是两平行直线被截得到，故①错误；
②在同一平面内，过一点有且只有一条直线与已知直线垂直，故②错误；
③若，，则，故③正确．
④负数没有平方根，故④错误．
综上所述，正确的只有③，共个．
故选：A．
【点睛】本题考查了三线八角中的同位角，平行公理，直线的交点及平行线的性质，平方根和立方根的概念，熟练掌握定义和概念是解题的关键．
5．A
【分析】根据平行线的定义、平行公理、对顶角的概念以及点到直线的距离的概念进行判断即可．
【详解】解：（1）过已知直线外一点有且只有一条直线与已知直线平行，说法（1）错误；
（2）相等的两个角不一定是对顶角，对顶角是在两直线相交的前提条件下形成的，故说法（2）错误；
（3）直线外一点到这条直线的垂线段的长度，叫做这点到直线的距离，点到直线的距离是一个长度，而不是一个图形，故说法（3）错误；
（4）同一平面内，不相交的两条直线叫做平行线，故说法（4）错误；
（5）同一平面内，垂直于同一条直线的两条直线平行，故说法（5）错误．
故说法正确的有0个．
故选：A．
【点睛】本题主要考查了相交线与平行线的一些基本概念，解题时注意：对顶角是相对于两个角而言，是指两个角的一种位置关系；点到直线的距离只能量出或求出，而不能说画出；平行公理中要准确理解“有且只有”的含义．
6．B
【分析】根据平行公理，垂线的基本性质进行判断即可．
【详解】解：∵在同一平面内，过直线外一点有且只有一条直线与已知直线平行；过一点有且只有一条直线与已知直线垂直，
∴小明错，小刚对，
故选：B．
【点睛】本题考查了平行公理，垂线的基本性质，熟练掌握基础知识点是解题的关键．
7．B
【分析】本题主要考查平行线的定义及平行公理，根据平行线的定义及平行公理进行判断．
【详解】解：①过直线外任意一点可作已知直线的一条平行线，故①不正确，
②同一平面内两条不相交的直线是平行线，故②正确；
③过已知直线外一点只能画一条直线与已知直线平行，故③正确；
④平行于同一直线的两直线平行，故④正确．
不正确的有①，共1个，
故选：B．
8．D
【分析】根据对顶角的含义可判断A，根据两点之间，线段最短可判断B，根据等角的补角的性质可得C，根据过直线外一点画已知直线的平行线可判断D，从而可得答案．
【详解】解：A、对顶角相等，正确；
B、两点之间所有连线中，线段最短，正确；
C、等角的补角相等，正确；
D、过直线外一点P，都能画一条直线与已知直线平行，错误；
故选：D．
【点睛】本题考查的是对顶角的性质，两点之间，线段虽短，等角的补角的性质，过直线外一点画已知直线的平行线，熟记基本概念与性质是解本题的关键．
9．A
【分析】本题考查了平行公理的推论，根据平行于同一条直线的两直线平行解答即可．
【详解】解：∵，
∴（平行于同一条直线的两直线平行）．
故选A．
10．C
【分析】根据直线与平面垂直的意义进行判断即可．
【详解】解：铅垂线、三角尺、合页型折纸可以检验直线与平面垂直，而长方形纸片比较单薄，不适合支撑检测直线与面之间的垂直度，
故选：C．
【点睛】本题考查垂线，掌握直线与平面垂直的意义是正确判断的前提．
11．C
【分析】分别根据对顶角以及平行公理和垂线的性质等知识，分别分析得出即可．
【详解】解：A、对顶角相等，原说法正确，故本选项不符合题意；
B、同角（等角）的余角相等，原说法正确，故本选项不符合题意；
C、过直线外一点有且只有一条直线与已知直线平行，原说法错误，故本选项符合题意；
D、过一点有且只有一条直线与已知直线垂直，原说法正确，故本选项不符合题意；
故选：C
【点睛】此题主要考查了命题与定理，正确把握相关定义是解题关键．
12．D
【分析】本题考查平行公理，根据“经过直线外一点，有且只有一条直线与已知直线平行”，分四种情况“当点P在边上且不与点O重合时；当点P在边上且不与点O重合时；当点P不在边或边上时；当点P与点O重合时”分别讨论可得答案．
【详解】解：当点P在边上且不与点O重合时，过点可以画一条直线与边平行；
当点P在边上且不与点O重合时，过点可以画一条直线与边平行；
当点P不在边或边上时，过点可以画一条直线与边平行，一条直线与边平行，共两条；
当点P与点O重合时，不存在过点P的直线与的边平行；
故选：D．
13．过直线外一点有且只有一条直线与这条直线平行
【分析】本题考查了平行公理，根据过直线外一点有且只有一条直线与这条直线平行解答即可，掌握平行公理是解题的关键．
【详解】解：理由是过直线外一点有且只有一条直线与这条直线平行，
故答案为：过直线外一点有且只有一条直线与这条直线平行．
14．1
【分析】本题考查了平行公理的知识点，解题的关键是理解并运用平行公理．
根据平行公理，经过直线外一点，有且只有一条直线与这条直线平行，据此确定过中点作平行于的直线的条数．
【详解】解：设的中点为，因为点在直线外，根据平行公理：经过直线外一点，有且只有一条直线与这条直线平行，所以过点画平行于的直线，这样的直线能画1条．
故答案为：1．
15． 平行 a b
【解析】略
16． 平行于同一条直线的两条直线平行
【分析】根据平行于同一条直线的两条直线平行即可得到答案．
【详解】解：∵直线，
∴（平行于同一条直线的两条直线平行）．
即三条直线，则，理由是平行于同一条直线的两条直线平行．
故答案为：，平行于同一条直线的两条直线平行
【点睛】此题考查了平行公理，熟练掌握平行公理是解题的关键．
17．①②④
【分析】根据平行公理及推论，垂线段最短以及平行线的判定与性质解答．
【详解】解：①过直线外一点有且只有一条直线与已知直线平行，故正确；
②已知直线a，b，c，若a∥b，b∥c，则a∥c，故正确；
③相等的角不一定是对顶角，故错误；
④直线外一点与直线上各点连接的所有线段中，垂线段最短，故正确；
故答案为：①②④．
【点睛】本题考查了平行公理及推论，垂线段最短以及平行线的判定与性质，熟记公理、推论是解题关键．
18．(1)见解析
(2)见解析
(3)C，BF；
【分析】（1）根据平行线的判定画出图形即可；
（2）根据垂线的定义画出图形即可；
（3）根据点到直线的距离的定义，画出图形即可．
【详解】（1）解：如图，直线CE即为所求；
（2）解：如图，直线BF即为所求；
（3）解：线段CF的长表示点C到线段BF的距离．
故答案为：C，BF；
【点睛】本题考查画平行线，垂线，点到直线的距离，掌握平行线的性质，点到直线的距离的定义是解题的关键．
19．(1)见解析
(2)见解析
(3)
【分析】本题考查了画平行线，画垂线，点到直线的距离．
（1）根据平行线的判定画出对应的平行线即可得到答案；
（2）根据垂直的定义画出对应的图形即可；
（3）根据点到直线的距离垂线段最短求解即可．
【详解】（1）解：如图，点即为所求
（2）解：如图，点，即为所求．
（3）由垂线段最短可知，线段＞线段．
故答案为：．
20．(1)见详解
(2)见详解
(3)见详解
(4)见详解
【分析】（1）作等边三角形OJK，延长JO到M，作∠JOK的角平分线ON，∠NOM即为所求；
（2）根据平行线的定义画出图形即可；
（3）根据垂线的定义画出图形即可；
（4）根据射线的定义以及题目要求画出图形即可．
【详解】（1）如图，∠MON即为所求；
（2）如图，直线AP即为所求；
（3）如图，垂线AB即为所求；
（4）如图，射线PO，点C即为所求．
【点睛】本题考查作图﹣复杂作图，垂线，平行线的性质等知识，解题的关键是掌握直线，射线，垂线，平行线的定义，属于中考常考题型．
21．(1)见解析
(2)见解析
(3)CP
【分析】（1）根据网格线互相平行可知，作图即可；
（2）根据垂直定义作图即可；
（3）根据点到直线的距离是垂线段的长度可求．
【详解】（1） 解：如图所示，MN即为所求；
（2）解：如图，PC即为所求；
（3）解：根据点到直线的距离是垂线段的长度，可知点C到直线OB的距离为线段CP的长度
故答案为：CP．
【点睛】本题考查了复杂作图，掌握平行线和垂线的画法、点到直线的距离的概念是解题的关键．
22．见解析
【分析】根据题目的要求直接画图即可．
【详解】解：如图，直线CD和直线EF即为所求作．
【点睛】本题考查作平行线和垂线，主要是考查学生的理解能力和动手操作能力，读懂作图语句，弄清所作图形的要求，结合对应几何图形的性质和基本作图方法是解答的关键．
23．(1)见解析，AB
(2)见解析
(3)见解析
【分析】（1）根据垂线的定义画出图形即可；
（2）根据垂线的定义画出图形；
（3）根据平行线的定义画出图形即可．
【详解】（1）解：如图，直线AB即为所求，线段AB的长是点A到直线的距离．
故答案为：AB
（2）如图，直线AC即为所求
（3）如图，直线AD即为所求
【点睛】本题考查作图 复杂作图，点到直线的距离，平行线的性质等知识，理解题意，灵活运用所学知识是解本题的关键．
24．(1)见解析
(2)见解析
(3)，见解析
【分析】本题考查了平行线的作法，以及平行公理，关键是掌握平行于同一条直线的两直线平行．
（1）根据平行线的定义画出图形；
（2）根据平行线的定义画出图形；
（3）根据平行于同一条直线的两直线平行解答即可．
【详解】（1）解：如图，直线即为所求，
（2）解：如图，直线即为所求，
（3）解：∵，，
∴（平行于同一条直线的两直线平行）．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)