6.3扇形统计图同步练习（含解析）

中小学教育资源及组卷应用平台
6.3扇形统计图
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，甲、乙、丙、丁四个扇形的面积之比是1：2：3：4，则甲、乙、丙、丁四个扇形中圆心角度数最小的是（ ）度
A．36 B．72 C．144 D．156
2．为了了解学生课外体育活动的情况，某校随机抽取了部分学生进行调查，将调查的数据进行统计并绘制成如图所示的扇形统计图和条形统计图．则被抽测学生中参加羽毛球项目的人数是（ ）
A．15人 B．20人 C．30人 D．40人
3．某单位有5名司机，分别用A、B、C、D、E表示，某月各位司机的耗油费用如下表，根据表中的数据制作统计图，为了更清楚地比较每位司机的耗油费用，应选择（ ）
司机 A B C D E
耗油费用 110元 120元 102元 150元 98元
A．条形统计图 B．扇形统计图
C．折线统计图 D．以上都不对
4．某校九(1)班的全体同学最喜欢的球类运动用如图所示的统计图来表示，下面说法正确的是( )

A．从图中可以直接看出喜欢各种球类的具体人数
B．从图中可以直接看出全班的总人数
C．从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况
D．从图中可以直接看出全班同学现在最喜欢各种球类的人数的大小关系
5．如图是某市来源统计图，则根据统计图得出的下列判断中，正确的是（ ）
A．汽车尾气所占百分比约为建筑扬尘的3倍
B．建筑扬尘占
C．煤炭燃烧释放的所对应扇形统计图的圆心角度数是
D．煤炭燃烧对的影响最大
6．某市的中考各科试卷总分为600分，其中数学为120分，若用扇形统计图画出各科分数比例，则数学所占扇形圆心角为（　　）度．
A．90 B．45 C．120 D．72
7．要想更清楚地了解各部分数量同总数之间的关系，应该选用（ ）
A．条形统计图 B．折线统计图 C．扇形统计图 D．直方图
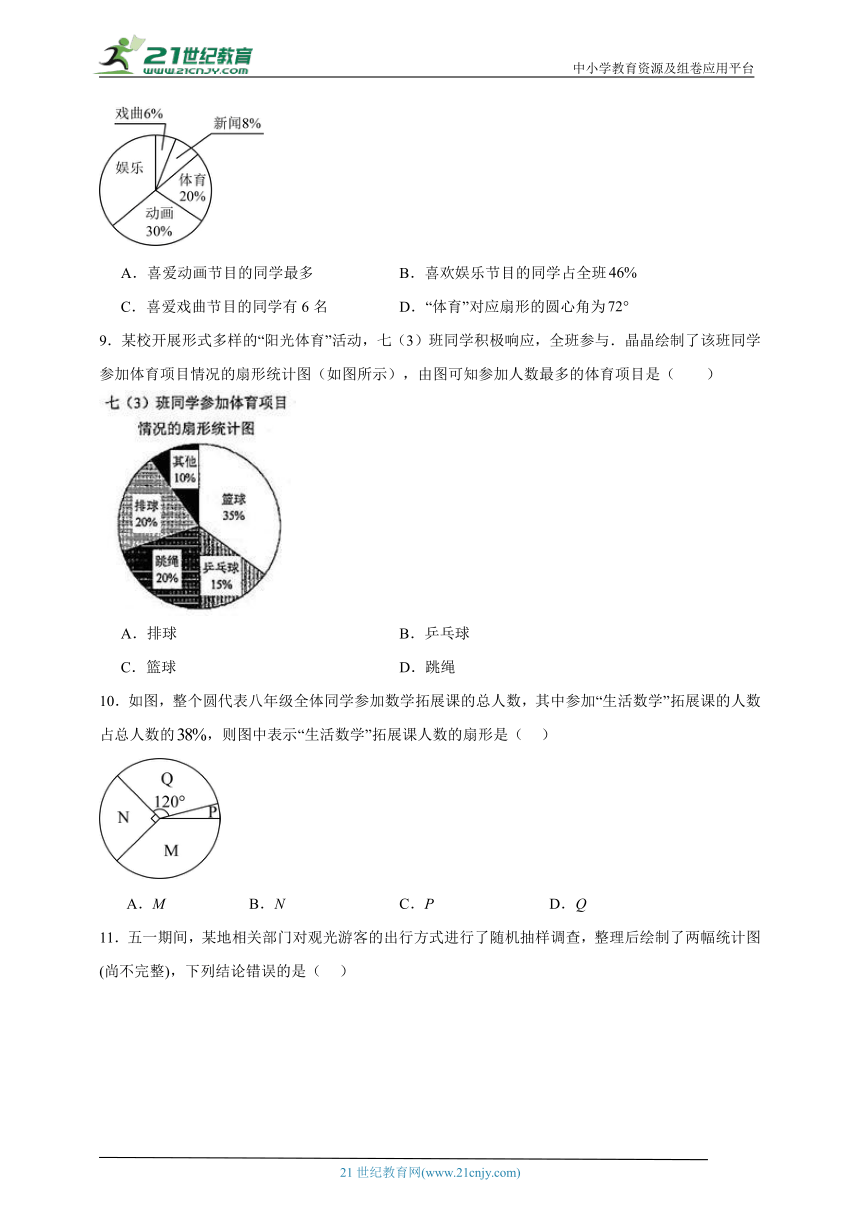
8．为了解全班同学对新闻，体育，动画，娱乐，戏曲五类节目的喜爱情况，班主任对全班50名同学进行了问卷调查（每名同学只选其中的一类），依据调查结果绘制了全班同学喜爱节目情况扇形统计图（如图所示）．下列说法正确的是（　　）
A．喜爱动画节目的同学最多 B．喜欢娱乐节目的同学占全班
C．喜爱戏曲节目的同学有6名 D．“体育”对应扇形的圆心角为
9．某校开展形式多样的“阳光体育”活动，七（3）班同学积极响应，全班参与．晶晶绘制了该班同学参加体育项目情况的扇形统计图（如图所示），由图可知参加人数最多的体育项目是（　　）
A．排球 B．乒乓球
C．篮球 D．跳绳
10．如图，整个圆代表八年级全体同学参加数学拓展课的总人数，其中参加“生活数学”拓展课的人数占总人数的，则图中表示“生活数学”拓展课人数的扇形是（ ）
A．M B．N C．P D．Q
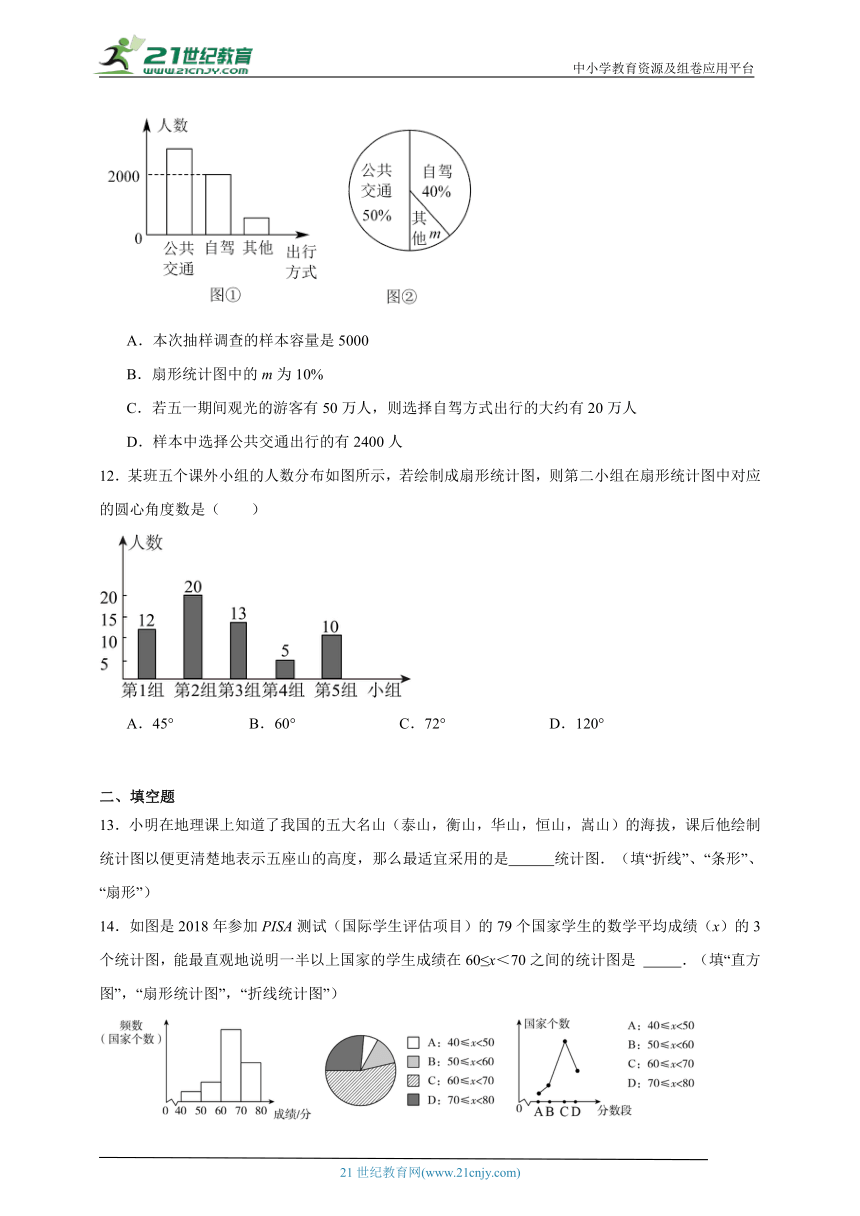
11．五一期间，某地相关部门对观光游客的出行方式进行了随机抽样调查，整理后绘制了两幅统计图(尚不完整)，下列结论错误的是（ ）
A．本次抽样调查的样本容量是5000
B．扇形统计图中的m为10%
C．若五一期间观光的游客有50万人，则选择自驾方式出行的大约有20万人
D．样本中选择公共交通出行的有2400人
12．某班五个课外小组的人数分布如图所示，若绘制成扇形统计图，则第二小组在扇形统计图中对应的圆心角度数是（　　）
A．45° B．60° C．72° D．120°
二、填空题
13．小明在地理课上知道了我国的五大名山（泰山，衡山，华山，恒山，嵩山）的海拔，课后他绘制统计图以便更清楚地表示五座山的高度，那么最适宜采用的是 统计图．（填“折线”、“条形”、“扇形”）
14．如图是2018年参加PISA测试（国际学生评估项目）的79个国家学生的数学平均成绩（x）的3个统计图，能最直观地说明一半以上国家的学生成绩在60≤x＜70之间的统计图是 ．（填“直方图”，“扇形统计图”，“折线统计图”）
15．为落实“五育并举”，某学校准备为学生打造第二课堂，有四类课程可供选择，分别是书画类，文艺类，社会实践类，体育类，现随机抽取了七年级部分学生对报名意向进行调查，并根据调查结果绘制了一幅不完整的扇形统计图，则在抽样的学生中，扇形所对应的圆心角的度数为 ．

16．期末考试后，小红将本班50名学生的数学成绩进行分类统计，得到如图的扇形统计图，则优生人数为 ．
17．如图是根据我县教育局网站上公布的某初中为玉树地震灾区捐款的情况而制作的统计图，已知该校在校学生有人，请根据统计图计算该校共捐款 元．
三、解答题
18．受疫情影响，2022年下半学期很多学校都纷纷响应了“停课不停学”的号召，开展线上教学活动，为了解学生上网课使用的设备类型，某校从“电脑，手机，电视，其他”四种类型的设备对学生进行了一次抽样调查；调查结果显示，每个学生只选择了以上四种设备类型中的一种，现将调查的结果绘制成如下两幅不完整的统计图：
请根据以上信息解答下列问题：
(1)本次调查抽取的总人数是________人，在扇形统计图中，“电视”所对应的扇形的圆心角的度数为________；
(2)补全条形统计图；
(3)该校九年级共有1200名学生，估计有多少名同学用电脑上课？
19．某校为满足学生的阅读需求，欲购进一批学生喜欢的图书，学校组织学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文史类”“社科类”“小说类”“生活类”中选择自己喜欢的一类．根据调查结果绘制了如图①②所示的统计图（未完成），请根据图中信息，解答下列问题：
(1)此次共调查了______名学生；
(2)将条形统计图补充完整；
(3)图②中“小说类”所在扇形的圆心角为______；
(4)若该校共有学生2000人，估计该校喜欢“社科类”图书的学生人数．
20．一块的菜地种植了4种蔬菜，分布情况如下图．若黄瓜的种植面积是450m2，则西红柿的面积比芹菜多多少平方米？
21．如图，这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图，但负责画此图的同学忘记了最喜爱篮球运动的人数．
(1)请你求出图中的x值；
(2)如果该年级最喜爱跳绳运动的同学有144人，那么这个年级共有多少人？
22．某校为了调查学生视力变化情况，从该校2010年入校的学生中抽取了部分学生进行连续三年的视力跟踪调查，将所得数据进行处理，制成折线统计图和扇形统计图（如图1、图2所示）．
（1）该校被抽查的学生共有多少名？
（2）现规定视力达到5.0及以上为合格，若被抽查年级共有500名学生，估计该年级在2012年有多少名学生视力合格．
23．某中学积极组织学生开展课外阅读活动，为了解本校学生每周课外阅读的时间量t（单位：小时），采用随机抽样的方法抽取部分学生进行了问卷调查，调查结果按0≤t＜2，2≤t＜3，3≤t＜4，t≥4分为四个等级，并分别用A、B、C、D表示，根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：
（1）求出x的值和抽取的学生人数;
（2）将不完整的条形统计图补充完整；
（3）若该校共有学生2500人，试估计每周课外阅读时间量满足2≤t＜4的人数.
24．如图，把一个圆分成四个扇形，求这四个扇形的圆心角的度数．
《6.3扇形统计图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C A D C D C D C A
题号 11 12
答案 D D
1．A
【分析】先设甲、乙、丙、丁的圆心角分别为α、β、γ、δ，根据扇形面积得出α：β：γ：δ=1：2：3：4，利用周角360°分别求出α=，β=2α=72°，γ=3α=108°，δ=4α=144°即可．
【详解】解；设甲、乙、丙、丁的圆心角分别为α、β、γ、δ，
∴S甲=，S乙=，S丙=，S丁=，
∵S甲：S乙：S丙：S丁=1：2：3：4，
∴：：：=1：2：3：4，
∴α：β：γ：δ=1：2：3：4，
∴α=，β=2α=72°，γ=3α=108°，δ=4α=144°，
故甲、乙、丙、丁四个扇形中圆心角度数最小的是36°．
故选A．
【点睛】本题主要考查了求扇形圆心角度数，解题的关键在于能够根据题意分别求出四个区域的圆心角度数．
2．C
【分析】本题考查的是条形统计图和扇形统计图的综合运用．结合参加足球的人数与其所占的百分比， 计算可得本次调查共抽取的学生数， 进而求出被抽测学生中参加羽毛球项目人数，即可．
【详解】解：根据题意得：被抽测学生总人数为人，
∴被抽测学生中参加羽毛球项目的人数是人．
故选：C
3．A
【分析】根据条形统计图可以清楚地表明各种数量的多少；扇形统计图可以比较清楚地反映出部分与部分、部分与整体之间的数量关系；折线统计图能够显示数据的变化趋势，反映事物的变化情况；进行判断即可．
【详解】解：由题意知，为了更清楚地比较每位司机的耗油费用的多少，应选择条形统计图
故选A．
【点睛】本题考查了统计图的特点．解题的关键在于熟练掌握统计图的特点．
4．D
【分析】利用扇形统计图的特点，可以得到各类所占的比例，但总数不确定，不能确定每类的具体人数．
【详解】解：因为扇形统计图直接反映部分占总体的百分比大小，不能反映具体数量的多少和变化情况，所以A、B、C都错误．
故答案为：D
【点睛】考点：扇形统计图．
5．C
【分析】本题主要考查扇形统计图，正确获取扇形统计图中的信息是解题关键．根据扇形统计图中的进行计算，然后再逐项判断即可．
【详解】解：A．建筑扬尘占，汽车尾气所占百分比约为建筑扬尘的5倍，故此选项不符合题意；
B．建筑扬尘占，故此选项不符合题意；
C.，即煤炭燃烧释放的所对应扇形统计图的圆心角度数是，故此选项符合题意；
D．汽车尾气排放对的影响最大，故此选项不符合题意．
故选：C．
6．D
【详解】试题解析：根据题意得：360°×=72°．
所以数学所占扇形圆心角为72度．
故选D．
7．C
【分析】根据题意的要求，结合统计图的特点，易得答案．
【详解】解：根据题意，要求能清楚地看出各部分数量与总数之间的关系，结合统计图的特点，易得应选用扇形统计图，
故选：C．
【点睛】本题考查的是统计图的选择，注意扇形统计图能清楚地看出各部分与总数之间的百分比关系．
8．D
【分析】本题考查了扇形统计图，从扇形统计图中正确获取信息是解题关键．根据全班共50名学生，班主任制作了50份问卷调查，可知班主任采用的是普查，由此可判断A；根据喜爱娱乐节目的同学所占的百分比最多，可判断B；用50乘以喜爱戏曲节目的同学所占的百分比计算出喜爱戏曲节目的同学的人数，可判断C；用乘以“体育”所占的百分比求出“体育”对应扇形的圆心角的度数，即可判断D．
【详解】解：全班共50名学生，班主任制作了50份问卷调查，所以班主任采用的是全面调查，喜爱娱乐的同学占比，所以喜爱娱乐节目的同学最多，故A、B选项错误；
喜爱戏曲节目的同学有名，故C选项错误；
“体育”对应扇形的圆心角为．故D选项正确．
故选：D．
9．C
【详解】考点：扇形统计图．
分析：因为总人数是一样的，所占的百分比越大，参加人数就越多，从图上可看出篮球的百分比最大，故参加篮球的人数最多．
解：∵篮球的百分比是35%，最大．
∴参加篮球的人数最多．
故选C．
10．A
【分析】首先根据扇形Q的圆心角为可得参加此类课的人数约占总数的，再根据，可得扇形的面积一定比Q大，根据图可选出答案．
【详解】解：∵扇形Q的圆心角为，
∴表示参加此类课的人数占总数的：，
∵，
∴扇形的面积一定比Q大，
∴图中表示“生活数学”拓展课人数的扇形是M，
故选：A．
【点睛】此题主要考查了扇形统计图，关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．用整个圆的面积表示总数（单位1），用圆的扇形面积表示各部分占总数的百分数．
11．D
【分析】结合条形图和扇形图，求出样本人数，进而进行解答．
【详解】解：A、本次抽样调查的样本容量是，正确，不符合题意；
B、 故扇形图中的m为10%，正确，不符合题意；
C、若“五一”期间观光的游客有50万人，则选择自驾方式出行的有50×40%=20万人，正确，不符合题意；
D、样本中选择公共交通出行的有5000×50%=2500人，错误，符合题意；
故选：D．
【点睛】本题考查了频数分布直方图、扇形统计图，熟悉样本、用样本估计总体是解题的关键，另外注意学会分析图表．
12．D
【分析】根据条形统计图即可得第二小组所占总体的比值，再乘以360°即可.
【详解】解：第二小组在扇形统计图中对应的圆心角度数是360°×＝120°，
故选D．
【点睛】本题考查的是条形统计图和扇形统计图的知识，难度不大，属于基础题型，明确求解的方法是解题的关键.
13．条形
【分析】根据条形统计图，扇形统计图和折线统计图的特点来判断即可．
【详解】解：为了便于清楚地表示五座山的高度，那么最适宜采用的是条形统计图，
故答案为：条形．
【点睛】本题考查统计图的选择，弄清统计图的特征是解题的关键．
14．扇形统计图
【分析】根据扇形统计图和频数分布直方图的意义选择．
【详解】解：根据扇形统计图直接反映部分占总体的百分比大小，
可知学生成绩在60≤x＜70之间的占一半以上，
所以能很好地说明一半以上国家的学生成绩在60≤x＜70之间的是扇形统计图；
故答案为：扇形统计图．
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力．利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
15．/144度
【分析】用乘以扇形统计图中D所占的百分比即可．
【详解】解：扇形所对应的圆心角的度数为；
故答案为：．
【点睛】本题考查了扇形统计图，属于应知应会题型，掌握求解的方法是关键．
16．10
【详解】试题解析：50×（1-16%-36%-28%）
=50×20%
=10（人）．
故优生人数为10人.
17．12590
【分析】根据扇形统计图中的数据求出各年级人数，再根据条形统计图中的数据求出各年级捐款数，各年级相加即可得到该校捐款总数．
【详解】解：1000×32%×15=4800元；
1000×33%×13=4290元；
1000×35%×10=3500元；
∴该校学生共捐款4800+4290+3500=12590元．
故答案为：12590．
【点睛】此题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
18．(1)100；；
(2)见解析；
(3)480名
【分析】（1）根据使用电脑的人数和所占的百分比即可求出总人数；用使用电视的人数所占的百分比乘以即可求出圆心角；
（2）利用总人数减去其他选项的人数，得到使用手机的人数，补全条形统计图即可；
（3）用九年级总人数乘以样本中使用电脑的人数所占的百分比，即可进行估算．
【详解】（1）解：本次调查抽取的总人数是（人），
“电视”所对应的扇形的圆心角的度数为，
故答案为：100；；
（2）解：使用手机的人数为（人），
补全条形统计图如下：
（3）解：（人），
即有480名同学用电脑上课．
【点睛】本题考查了条形统计图，扇形统计图，样本估计总体等知识，从图表中正确识别信息是解题关键．
19．(1)200
(2)图见解析
(3)126
(4)估计该校喜欢“社科类”图书的学生人数为240人
【分析】（1）根据选择“文史类”的学生的扇形统计图和条形统计图的信息即可得；
（2）先结合（1）的结果求出选择“生活类”的学生人数，再求出选择“小说类”的学生人数，据此补全条形统计图即可得；
（3）利用乘以选择“小说类”的学生所占百分比即可得；
（4）利用全校学生总人数乘以喜欢“社科类”图书的学生所占百分比即可得．
【详解】（1）解：此次调查的学生总人数为（名），
故答案为：200．
（2）解：选择“生活类”的学生人数为（名），
选择“小说类”的学生人数为（名），
则补全条形统计图如下：
（3）解：图②中“小说类”所在扇形的圆心角为，
故答案为：126．
（4）解：（人），
答：估计该校喜欢“社科类”图书的学生人数为240人．
【点睛】本题考查了条形统计图和扇形统计图的信息关联、利用样本估计总体等知识点，熟练掌握统计调查的相关知识是解题关键．
20．
【分析】根据黄瓜的种植面积和所占的百分比，求出菜地的总面积，再根据西红柿和芹菜种植面积的百分比求出种植西红柿和芹菜的面积，即可解答．
【详解】由图可知：黄瓜种植面积占菜地总面积的，西红柿种植面积占菜地总面积的，芹菜种植面积占菜地总面积的，
黄瓜的种植面积是
菜地的总面积为
西红柿种植面积为，芹菜种植面积为
答：西红柿的面积比芹菜的面积多
【点睛】本题考查了扇形统计图，以及求一个数的百分比，解题关键是读懂扇形统计图，正确计算．
21．(1)79°
(2)540
【分析】（1）用360°减去其他几项所对的圆心角的度数，即可求解；
（2）根据喜爱跳绳的同学除以跳绳的圆心角所占的比例，可得答案．
【详解】（1）解：x=360°﹣70°﹣65°﹣50°﹣96°=79°；
（2）解：这个年级共有144÷=540人．
【点睛】本题主要考查了扇形统计图，用样本估计总体，根据题意，能从统计图中获取准确信息是解题的关键．
22．（1）该校被抽查的学生共有300名；（2）估计该年级在2012年有300名学生视力合格．
【分析】（1）利用折线图中10年的视力为5.0以下人数120和扇形图中的百分比40%，即可求出总人数；
（2）用样本估计总体可直接求算结果．
【详解】解：（1）120÷40%=300人．
故该校被调查的学生共有300名．
（2）500×（10%+20%+30%）=300人．
估计该年级在2012年有300名视力合格．
【点睛】本题考查的是折线统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．
23．（1）30；200人；（2）作图见解析；（3）1000人.
【详解】试题分析：（1）根据所有等级的百分比的和为1，则可计算出x的值；由条形图可知A等级有90人，由扇形图可知对应的百分比为45%，那么抽查的学生总数=A等级的人数÷对应的百分比，计算即可求解；
（2）再求出B级与C级的人数，即可作图；
（3）利用每周课外阅读时间量满足2≤t＜4的人数=该校总人数×B级的与C级百分比的和计算即可．
试题解析：（1）∵x%+15%+10%+45%=1，
∴x=30；
调查的总人数=90÷45%=200（人）
（2）B等级人数=200×30%=60（人）；C等级人数=200×10%=20（人），
（3）2500×（10%+30%）=1000（人），
所以估计每周课外阅读时间量满足2≤t＜4的人数为1000人
【点睛】本题主要考查了条形统计图，扇形统计图及用样本估计总体．解题的关键是读懂统计图，能从条形统计图，扇形统计图中得到准确的信息．
24．扇形甲：；扇形乙：；扇形丙：；扇形丁：．
【分析】此题考查了扇形所占的百分比和扇形圆心角之间的关系，分别用360度乘以每个扇形中的百分数即可得答案.
【详解】解：扇形甲的圆心角度数为．
扇形乙的圆心角度数为．
扇形丙的圆心角度数为.
扇形丁的圆心角度数为：
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)