七下整式乘除复习优质课课件

课件14张PPT。诸暨荣怀学校初中部 王航燕整式的乘除
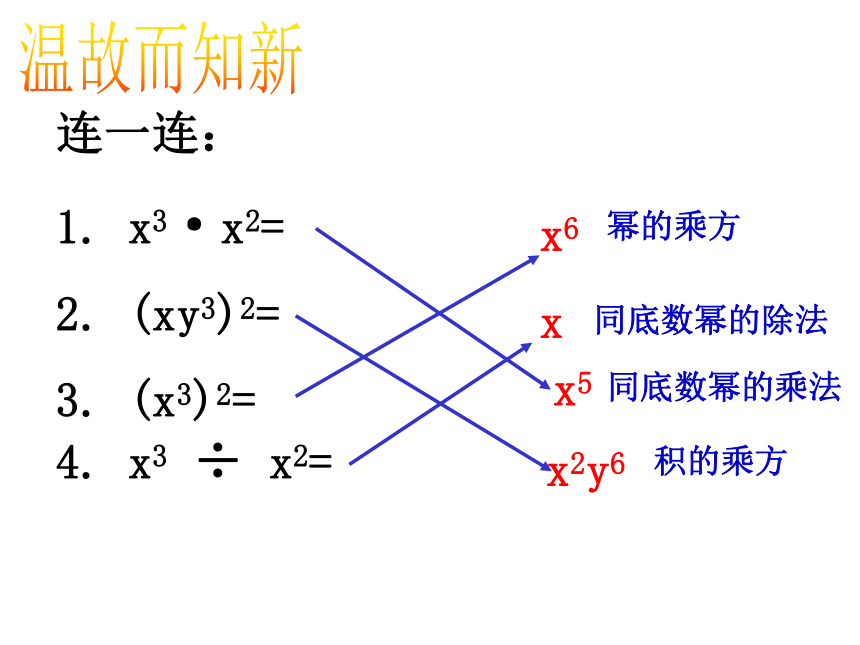
复习连一连：
1. x3·x2=
2. (xy3)2=
3. (x3)2= 4. x3 ÷ x2=x5x6xx2y6同底数幂的乘法幂的乘方同底数幂的除法积的乘方温故而知新计算：小试牛刀2、(a+2b)(a+2b)1、(2a3)2·a+2a 15÷(a 4) 21、下列各式中能否用公式计算，若能，则用什么公式？
(1)(2a＋3b)(3b－2a) (2)(x－y)(﹣x－y)
(3) (x＋y)(﹣x－y) (4)(2X－3Y)(2Y＋3X）
火眼金睛2.下列各式中,运算结果是x2－36y2的是( )A (﹣6y－x)(6y－x) B(﹣6y＋x)(6y－x)
C (x＋4y)(x－9y) D (-6y＋x)(﹣6y－x)A火眼金睛3.已知(x＋a)2 =x2－8x＋b,则（ ）
A、a=4 ， b=16 B、a=4， b=﹣16
C、a=﹣4 ，b=16 D、a= ﹣4 ，b= ﹣16C火眼金睛1、当x= 时，求代数式：
(2x＋5)2－(2x－1)(2x＋1)的值。夯实基础： 2 .已知a+b=5 ，ab= -2，求a2+b2 的值∴ a2+b2=(a+b)2-2ab=25 -（-4）=29完全平方公式 的变形应用
解：∵ (a+b)2 = a2+2ab+b2活用公式(a-b)2∵(a-b)2=(a+b)2-4ab∴(a-b)2=52-4×（-2）
=25+8
=33，求a2+b2 的值
变式：已知(a+b-5)2+ ab+2 =0，求(a-b)2的值整体代入3、活用公式4、已知(2016-a)(2014-a )=2015,
求(2016-a)2+(2014-a)2的值拓展思维变式： (3+1)(32+1)(34+1)···(364+1)的
值是 。 数(2-1) (2+1)(22+1)(24+1)···(264+1)的
值是 ________数构造平方差
公式(3-1)1/22128— 1已知x≠1，(1+x)(1-x)=1-x2
(1-x)(1+x+x2)=1-x3
(1-x)(1+x+x2+x3)=1-x4 利用平方差公式探究n次方差公式公式推广1-xn+1-632n+1-2x100-11、观察以上各式并猜想
(1-x)(1+x+x2+….+xn)= ; 2、根据你的猜想计算：
(1)(1-2)(1+2+22+23+24+25)= ; (2)2+22+23…+2n= ; (n为正整数)(3)(x-1)(x99+x98+x97…+x2+x+1)= ; Thank You!课 堂 小 结今天这堂课我们主要复习了哪几部分知识？
通过这次复习你有什么新的收获？具体是什么？
相比之前的学习你哪些方面得到了提高？
已知x≠1，(1+x)(1-x)=1-x2
(1-x)(1+x+x2)=1-x3
(1-x)(1+x+x2+x3)=1-x4 1、观察以上各式并猜想
(1-x)(1+x+x2+….+xn)= ; 2、根据你的猜想计算：
(1)(1-2)(1+2+22+23+24+25)= ; (2)2+22+23…+2n= ; (n为正整数)(3)(x-1)(x99+x98+x97…+x2+x+1)= ; 公式推广利用平方差公式探究n次方差公式我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如下图）
1
1 1
1 2 1
1 3 3 1
…(从第三行开始，每行的首尾两个数以外的各数都等于它上方两个数的和）此图揭示了(a+b) n(n为非负整数）展开式的项数及各项系数的有关规律，例如：
(a+b) 0=1,它只有一项，系数为1
(a+b) 1=a+b,它有两项，系数为1,1，系数和为2
(a+b) 2 =a2+2ab+b2，它有三项，系数为1,2,1，系数和为4
(a+b) 3=a3+3a2b+3ab2+b3,它有四项，系数为1,3,3,1，系数和为8….
利用完全平方公式探究n次方展开式根据以上规律，解答下列问题：
（1）(a+b) 4展开式共有 项，系数分别为 ；
（2）(a+b) n展开式共有 项，系数和为 ；
（3）计算(x-2y) 5
公式推广