浙教版七年级下册 3.1 同底数幂的乘法 课件(共17张PPT)
文档属性
| 名称 | 浙教版七年级下册 3.1 同底数幂的乘法 课件(共17张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-11 00:00:00 | ||
图片预览







文档简介
(共17张PPT)
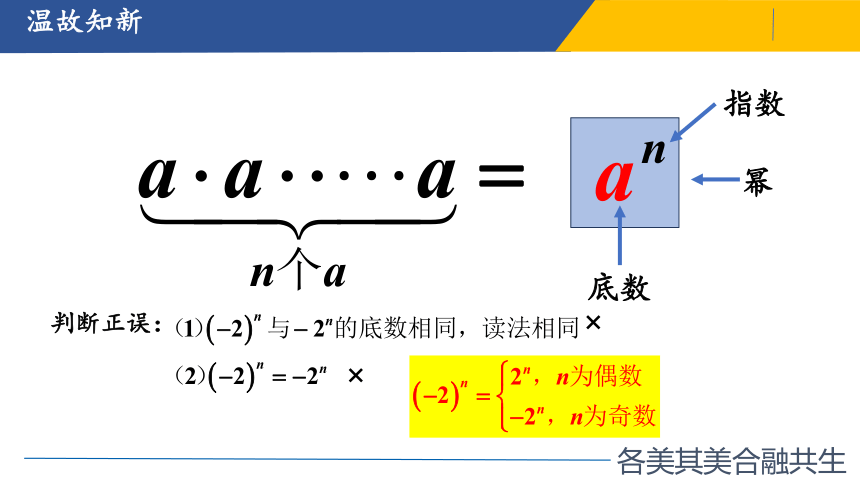
温故知新
幂
底数
指数
判断正误:
探究新知
2024年5月10日,记者从中国科学院国家天文台获悉,“中国天眼”FAST近期发现了6个距离地球约50亿光年的中性氢星系,这是人类迄今直接探测到的最远的一批中性氢星系.
光年是长度单位,1光年是是光在真空中传播一年所经过的距离.若1年以秒计算,则1光年大约多少米?(光的速度大约是米/秒,结果用科学计数法表示)
探究新知
底数相同
同底数幂
3.1 同底数幂的乘法(1)
浙教版七下数学
探究新知
(乘方的定义)
(乘法结合律)
(乘方的定义)
下列各式中,属于同底数幂相乘的有哪些?
探究新知
探究新知
其中,都是正整数
同底数幂的乘法法则
同底数幂相乘,底数不变,指数相加。
例题讲解
例1:计算,结果用幂的形式表示.
⑴(-8)×(-8)15;
⑵221 ×(-2)79;
⑶(x-y)·(y-x)5;
⑷125 × 53m ×(-5)2m-1(m是正整数);
方法总结:
1、单独的数字或字母的指数是1;
2、底数互为相反数时,先尝试转化再应用法则;
3、法则中的底数既可以是单项式,也可以是多项式。
当堂练习
计算,结果用幂的形式表示.
⑴() ×()2 ×()3····()99 ×()100;
⑵-22 ×(-2)3 × 25;
⑶(a-2b)·(2b-a)2·(2b-a)3;
⑷-62m ×(-6)2m+1;(m是正整数)
(5) (a+b-c)·(c-a-b)3
例题讲解
例2:我国“神威太湖之光”超级计算机是全球第一台运行速度超过10亿亿次/秒的超级计算机,峰值性能高达12.54亿亿次/秒,持续性能达到9.3亿亿次/秒.这套系统1分钟的计算能力,相当于全球72亿人同时用计算器不间断计算32年。如果按10亿亿次/秒速度工作一整天,那么它能运算多少次 (结果用科学计数法表示)
例题讲解
例2:如果按10亿亿次/秒速度工作一整天,那么它能运算多少次 (结果用科学计数法表示)
分析:
答:它一天能运算 次.
解:
当堂练习
宁波市约有400万户居民,平均每户有两个水龙头,估计其中有的水龙头漏水,若每个漏水水龙头1秒钟漏一滴水,10滴水约重1克,试问该城市一天约漏掉多少克水?(结果用科学计数法表示)
解:
答:该城市一天约漏掉 克.
高阶思维
逆用法则: am+n = am · an (m、n都是正整数)
1、已知4x=8,4y=2,则4x+y的值是________;
2、若a3=m,a5=n,用含m,n的整式表示a11为_________;
3、已知xa=2,xb=4,xc=8(a,b,c为正整数),请和你的同桌交流并提出要一个数学问题 。
(1)已知a+b-2=0,则3a·3b的值为______;
(2)已知3a·32b =27,且为非负整数,则的值为______;
(3) 若2m+2m+2m+2m=128,则m=__________;
高阶思维
课堂小结
同底数幂的乘法
一个
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
推广:am·an·ap=am+n+p (m,n,p都是正整数)
直接应用法则
底数相同时
底数不相同时
先变成同底数,再应用法则
三种思想
整体思想
从特殊到一般,再从一般到特殊
方程思想
作业
1. 作业本1:3.1同底数幂的乘法(1)
再见
温故知新
幂
底数
指数
判断正误:
探究新知
2024年5月10日,记者从中国科学院国家天文台获悉,“中国天眼”FAST近期发现了6个距离地球约50亿光年的中性氢星系,这是人类迄今直接探测到的最远的一批中性氢星系.
光年是长度单位,1光年是是光在真空中传播一年所经过的距离.若1年以秒计算,则1光年大约多少米?(光的速度大约是米/秒,结果用科学计数法表示)
探究新知
底数相同
同底数幂
3.1 同底数幂的乘法(1)
浙教版七下数学
探究新知
(乘方的定义)
(乘法结合律)
(乘方的定义)
下列各式中,属于同底数幂相乘的有哪些?
探究新知
探究新知
其中,都是正整数
同底数幂的乘法法则
同底数幂相乘,底数不变,指数相加。
例题讲解
例1:计算,结果用幂的形式表示.
⑴(-8)×(-8)15;
⑵221 ×(-2)79;
⑶(x-y)·(y-x)5;
⑷125 × 53m ×(-5)2m-1(m是正整数);
方法总结:
1、单独的数字或字母的指数是1;
2、底数互为相反数时,先尝试转化再应用法则;
3、法则中的底数既可以是单项式,也可以是多项式。
当堂练习
计算,结果用幂的形式表示.
⑴() ×()2 ×()3····()99 ×()100;
⑵-22 ×(-2)3 × 25;
⑶(a-2b)·(2b-a)2·(2b-a)3;
⑷-62m ×(-6)2m+1;(m是正整数)
(5) (a+b-c)·(c-a-b)3
例题讲解
例2:我国“神威太湖之光”超级计算机是全球第一台运行速度超过10亿亿次/秒的超级计算机,峰值性能高达12.54亿亿次/秒,持续性能达到9.3亿亿次/秒.这套系统1分钟的计算能力,相当于全球72亿人同时用计算器不间断计算32年。如果按10亿亿次/秒速度工作一整天,那么它能运算多少次 (结果用科学计数法表示)
例题讲解
例2:如果按10亿亿次/秒速度工作一整天,那么它能运算多少次 (结果用科学计数法表示)
分析:
答:它一天能运算 次.
解:
当堂练习
宁波市约有400万户居民,平均每户有两个水龙头,估计其中有的水龙头漏水,若每个漏水水龙头1秒钟漏一滴水,10滴水约重1克,试问该城市一天约漏掉多少克水?(结果用科学计数法表示)
解:
答:该城市一天约漏掉 克.
高阶思维
逆用法则: am+n = am · an (m、n都是正整数)
1、已知4x=8,4y=2,则4x+y的值是________;
2、若a3=m,a5=n,用含m,n的整式表示a11为_________;
3、已知xa=2,xb=4,xc=8(a,b,c为正整数),请和你的同桌交流并提出要一个数学问题 。
(1)已知a+b-2=0,则3a·3b的值为______;
(2)已知3a·32b =27,且为非负整数,则的值为______;
(3) 若2m+2m+2m+2m=128,则m=__________;
高阶思维
课堂小结
同底数幂的乘法
一个
法则
am·an=am+n (m,n都是正整数)
注意
同底数幂相乘,底数不变,指数相加
推广:am·an·ap=am+n+p (m,n,p都是正整数)
直接应用法则
底数相同时
底数不相同时
先变成同底数,再应用法则
三种思想
整体思想
从特殊到一般,再从一般到特殊
方程思想
作业
1. 作业本1:3.1同底数幂的乘法(1)
再见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
