第五章 分式 单元复习课件(共36张PPT)
文档属性
| 名称 | 第五章 分式 单元复习课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:15:34 | ||
图片预览









文档简介
(共36张PPT)
(浙教版)七年级
下
单元复习
分式
第5章
“五”
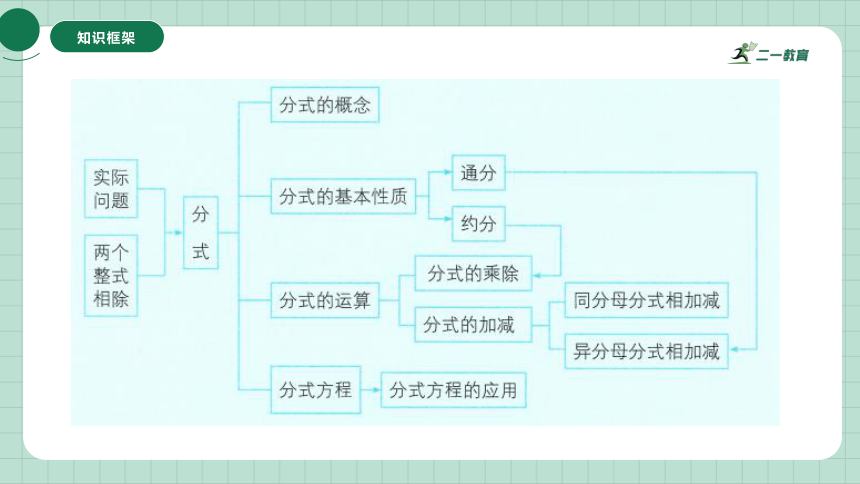
知识框架
知识点1 分式
1.分式:
这些代数式都表示两个整式相除,且除式中含有字母。像这样的代数式叫作分式。
分式必须满足三个条件:
①具备的形式;, 都是整式;③分母中含有字母。三个条件缺一不可。
知识梳理
知识点1 分式
2.分式有无意义的条件:
知识梳理
分式中字母的取值不能使分母为零。当分母的值为零时,分式就没有意义。
分类 条件
. .
典例精练
B
D
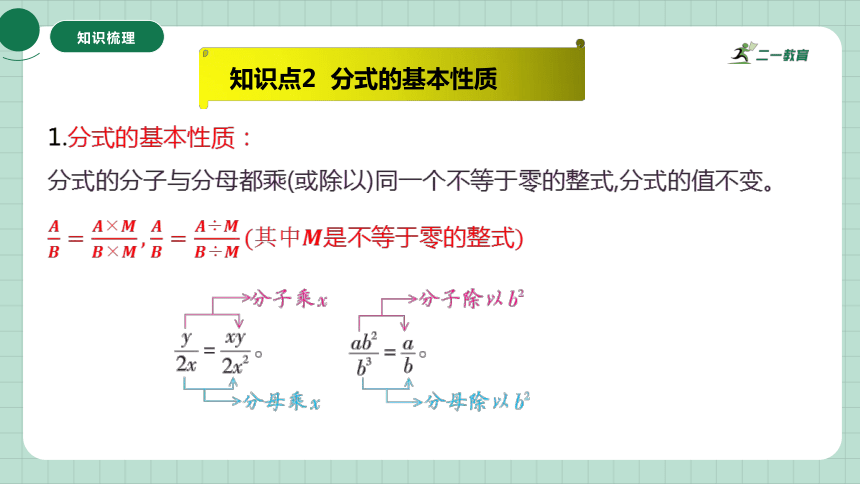
知识点2 分式的基本性质
1.分式的基本性质:
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变。
知识梳理
知识点2 分式的基本性质
2.分式的符号法则:
分式的分子、分母及分式的本身,任意改变其中的两个符号,分式的值不变;若只改变其中的一个或三个全变号,则分式的值变成原分式值的相反数.
, 。
知识梳理
知识点2 分式的基本性质
3.分式的约分:
把一个分式的分子和分母的公因式约去,叫做分式的约分.
注意:要约去分子、分母的所有公因式.
最简分式:分子分母没有公因式的分式,叫做最简分式.
知识梳理
知识点2 分式的基本性质
3.分式的约分:
约分的方法:(1)若分子、分母都是单项式,则约去分子、分母系数的最大公因数和相同字母的最低次幂(公因式);
(2)若分子或分母中含有多项式,则先将多项式分解因式,然后
约去分子、分母所有的公因式。
注意:约分的最后结果是最简分式或整式。
知识梳理
知识点2 分式的基本性质
3.多项式除以多项式:
多项式除以多项式可转化为分式的约分,其依据是分式的意义和等
式的基本性质。最后的结果要用整式(整除时)或最简分式
(不整除时)表示。
知识梳理
典例精练
1.下列分式中,属于最简分式的是 ( )
A. B. C. D.
2.下列各式从左到右的变形正确的是( )
A. = B. = C. -= D. =
C
A
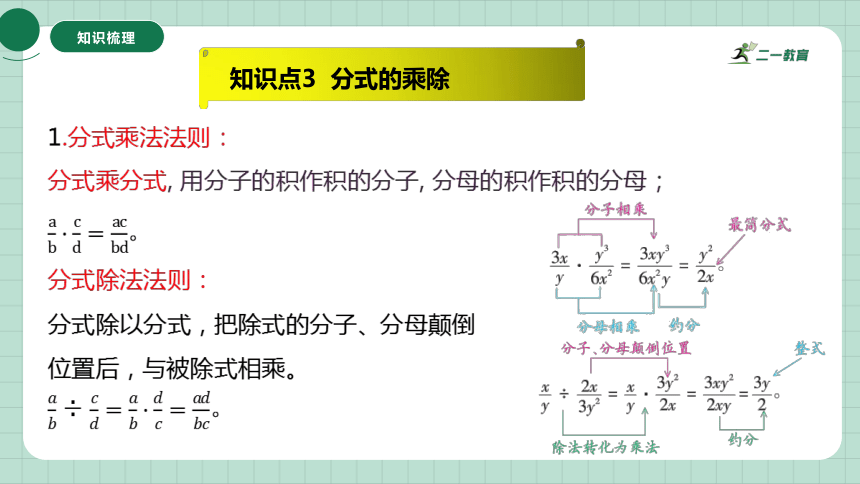
知识点3 分式的乘除
1.分式乘法法则:
分式乘分式, 用分子的积作积的分子, 分母的积作积的分母;
。
分式除法法则:
分式除以分式,把除式的分子、分母颠倒
位置后,与被除式相乘。
。
知识梳理
知识点3 分式的乘除
1.分式的乘方法则:
分式的乘方等于分子分母分别乘方.
是正整数 。
知识梳理
典例精练
C
D
知识点4 分式的加减
1.同分母分式的加减法:
同分母分式相加减,分母不变,把分子相加减。
。
同分母分式加减的基本步骤
1. 分母不变,把分子相加减.
(1)如果分式的分子是多项式,一定要加上括号;
(2)如果是分子式单项式,可以不加括号.
2. 分子相加减时,应先去括号,再合并同类项;
3. 最后的结果,应化为最简分式或者整式.
知识梳理
知识点4 分式的加减
2.分式的通分:
把分母不相同的几个分式化成分母
相同的分式,叫作通分。
确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
知识梳理
定系数
定因式
定指数
知识点4 分式的加减
3.异分母分式的加减法:
异分母分式的加减,先通分,变为同分母的分式,再加减.
。
异分母分式加减法的一般步骤:
(1)通分:将异分母分式化为同分母分式;
(2)加减:按同分母分式的加减法则进行加减运算;
(3)约分:把结果化成最简分式或整式。
知识梳理
典例精练
A
B
知识点5 分式方程
1.分式方程:
只含分式,或分式和整式,并且分母里含有未知数的方程叫作分式方程。
分式方程必须满足的条件(三者缺一不可)
(1) 是方程(含有未知数的等式);
(2) 含有分母;
(3) 分母中含有未知数.
知识梳理
知识点5 分式方程
2.分式方程的解法:
解分式方程的基本思路:将分式方程化为整式方程,具体做法是“去分母” 即方程两边同乘最简公分母.这也是解分式方程的一般方法.
解分式方程的一般步骤:
知识梳理
知识点5 分式方程
3.增根:
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解.我们称它为原方程的增根.
知识梳理
分式方程解的检验方法:
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
知识点5 分式方程
4.列分式方程解应用题的步骤 :
(1)审:审清题意;
(2)找:找出等量关系;
(3)设:设出未知数(直接设法、间接设法);
(4)列:用代数式表示等量关系,列出分式方程;
(5)解:解分式方程;
(6)检:必须检验根的正确性与合理性;
(7)答:写出答案.
知识梳理
典例精练
D
B
典例精练
D
A
典例精练
6.端午节,“味美早餐店”的粽子打9折出售,小红的妈妈去该店买粽子花了54元,比平时多买了3个,则平时每个粽子卖多少元?设平时每个粽子卖x元,则所列方程是____________.
D
提升训练
1. 已知=+,则下列变形正确的是( )
A. R= B. R=
C. R= D. R=R1+R2
2. 若m+n=1,则代数式·(m2-n2)的值为( )
A. -3 B. -1 C. 1 D. 3
B
D
提升训练
C
A
提升训练
5. 已知实数a,b互为倒数,则代数式的值为 .
6. 若x+=3,则的值为 .
7. 已知+=3,+=4,+=5,则= .
1
提升训练
提升训练
提升训练
解:根据题意得 a=1,b=-2,
∵|c+1|=3,∴c+1=3或c+1=-3,
解得c=2或c=-4,
又∵ac<0,∴c=-4,
提升训练
提升训练
11. 某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务,选派甲、乙两人分别用A,B两种外墙漆各完成总粉刷任务的一半.据测算需要A,B两种外墙漆各300千克,购买外墙漆总费用为15000元,已知A种外墙漆每千克的价格比B种外墙漆每千克的价格多2元.
(1) 求A,B两种外墙漆每千克的价格各是多少元.
(1) 设A种外墙漆每千克的价格是x元,B种外墙漆每千克的价格是y元.根据题意,得解得所以A种外墙漆每千克的价格是26元,B种外墙漆每千克的价格是24元
提升训练
(2) 已知乙每小时粉刷外墙的面积是甲每小时粉刷外墙的面积的,乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时.问:甲每小时粉刷外墙的面积是多少平方米
(2) 设甲每小时粉刷外墙的面积是m平方米,则乙每小时粉刷外墙的面积是m平方米.根据题意,得-=5,解得m=25.经检验,m=25是分式方程的解,且符合题意.所以甲每小时粉刷外墙的面积是25平方米
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(浙教版)七年级
下
单元复习
分式
第5章
“五”
知识框架
知识点1 分式
1.分式:
这些代数式都表示两个整式相除,且除式中含有字母。像这样的代数式叫作分式。
分式必须满足三个条件:
①具备的形式;, 都是整式;③分母中含有字母。三个条件缺一不可。
知识梳理
知识点1 分式
2.分式有无意义的条件:
知识梳理
分式中字母的取值不能使分母为零。当分母的值为零时,分式就没有意义。
分类 条件
. .
典例精练
B
D
知识点2 分式的基本性质
1.分式的基本性质:
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变。
知识梳理
知识点2 分式的基本性质
2.分式的符号法则:
分式的分子、分母及分式的本身,任意改变其中的两个符号,分式的值不变;若只改变其中的一个或三个全变号,则分式的值变成原分式值的相反数.
, 。
知识梳理
知识点2 分式的基本性质
3.分式的约分:
把一个分式的分子和分母的公因式约去,叫做分式的约分.
注意:要约去分子、分母的所有公因式.
最简分式:分子分母没有公因式的分式,叫做最简分式.
知识梳理
知识点2 分式的基本性质
3.分式的约分:
约分的方法:(1)若分子、分母都是单项式,则约去分子、分母系数的最大公因数和相同字母的最低次幂(公因式);
(2)若分子或分母中含有多项式,则先将多项式分解因式,然后
约去分子、分母所有的公因式。
注意:约分的最后结果是最简分式或整式。
知识梳理
知识点2 分式的基本性质
3.多项式除以多项式:
多项式除以多项式可转化为分式的约分,其依据是分式的意义和等
式的基本性质。最后的结果要用整式(整除时)或最简分式
(不整除时)表示。
知识梳理
典例精练
1.下列分式中,属于最简分式的是 ( )
A. B. C. D.
2.下列各式从左到右的变形正确的是( )
A. = B. = C. -= D. =
C
A
知识点3 分式的乘除
1.分式乘法法则:
分式乘分式, 用分子的积作积的分子, 分母的积作积的分母;
。
分式除法法则:
分式除以分式,把除式的分子、分母颠倒
位置后,与被除式相乘。
。
知识梳理
知识点3 分式的乘除
1.分式的乘方法则:
分式的乘方等于分子分母分别乘方.
是正整数 。
知识梳理
典例精练
C
D
知识点4 分式的加减
1.同分母分式的加减法:
同分母分式相加减,分母不变,把分子相加减。
。
同分母分式加减的基本步骤
1. 分母不变,把分子相加减.
(1)如果分式的分子是多项式,一定要加上括号;
(2)如果是分子式单项式,可以不加括号.
2. 分子相加减时,应先去括号,再合并同类项;
3. 最后的结果,应化为最简分式或者整式.
知识梳理
知识点4 分式的加减
2.分式的通分:
把分母不相同的几个分式化成分母
相同的分式,叫作通分。
确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.
知识梳理
定系数
定因式
定指数
知识点4 分式的加减
3.异分母分式的加减法:
异分母分式的加减,先通分,变为同分母的分式,再加减.
。
异分母分式加减法的一般步骤:
(1)通分:将异分母分式化为同分母分式;
(2)加减:按同分母分式的加减法则进行加减运算;
(3)约分:把结果化成最简分式或整式。
知识梳理
典例精练
A
B
知识点5 分式方程
1.分式方程:
只含分式,或分式和整式,并且分母里含有未知数的方程叫作分式方程。
分式方程必须满足的条件(三者缺一不可)
(1) 是方程(含有未知数的等式);
(2) 含有分母;
(3) 分母中含有未知数.
知识梳理
知识点5 分式方程
2.分式方程的解法:
解分式方程的基本思路:将分式方程化为整式方程,具体做法是“去分母” 即方程两边同乘最简公分母.这也是解分式方程的一般方法.
解分式方程的一般步骤:
知识梳理
知识点5 分式方程
3.增根:
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解.我们称它为原方程的增根.
知识梳理
分式方程解的检验方法:
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
知识点5 分式方程
4.列分式方程解应用题的步骤 :
(1)审:审清题意;
(2)找:找出等量关系;
(3)设:设出未知数(直接设法、间接设法);
(4)列:用代数式表示等量关系,列出分式方程;
(5)解:解分式方程;
(6)检:必须检验根的正确性与合理性;
(7)答:写出答案.
知识梳理
典例精练
D
B
典例精练
D
A
典例精练
6.端午节,“味美早餐店”的粽子打9折出售,小红的妈妈去该店买粽子花了54元,比平时多买了3个,则平时每个粽子卖多少元?设平时每个粽子卖x元,则所列方程是____________.
D
提升训练
1. 已知=+,则下列变形正确的是( )
A. R= B. R=
C. R= D. R=R1+R2
2. 若m+n=1,则代数式·(m2-n2)的值为( )
A. -3 B. -1 C. 1 D. 3
B
D
提升训练
C
A
提升训练
5. 已知实数a,b互为倒数,则代数式的值为 .
6. 若x+=3,则的值为 .
7. 已知+=3,+=4,+=5,则= .
1
提升训练
提升训练
提升训练
解:根据题意得 a=1,b=-2,
∵|c+1|=3,∴c+1=3或c+1=-3,
解得c=2或c=-4,
又∵ac<0,∴c=-4,
提升训练
提升训练
11. 某工程队承接了老旧小区改造工程中1000平方米的外墙粉刷任务,选派甲、乙两人分别用A,B两种外墙漆各完成总粉刷任务的一半.据测算需要A,B两种外墙漆各300千克,购买外墙漆总费用为15000元,已知A种外墙漆每千克的价格比B种外墙漆每千克的价格多2元.
(1) 求A,B两种外墙漆每千克的价格各是多少元.
(1) 设A种外墙漆每千克的价格是x元,B种外墙漆每千克的价格是y元.根据题意,得解得所以A种外墙漆每千克的价格是26元,B种外墙漆每千克的价格是24元
提升训练
(2) 已知乙每小时粉刷外墙的面积是甲每小时粉刷外墙的面积的,乙完成粉刷任务所需时间比甲完成粉刷任务所需时间多5小时.问:甲每小时粉刷外墙的面积是多少平方米
(2) 设甲每小时粉刷外墙的面积是m平方米,则乙每小时粉刷外墙的面积是m平方米.根据题意,得-=5,解得m=25.经检验,m=25是分式方程的解,且符合题意.所以甲每小时粉刷外墙的面积是25平方米
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
