第2章 《二元一次方程组》章节检测卷(含解析)七年级数学下册浙教版
文档属性
| 名称 | 第2章 《二元一次方程组》章节检测卷(含解析)七年级数学下册浙教版 |  | |
| 格式 | docx | ||
| 文件大小 | 798.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:42:40 | ||
图片预览




文档简介
第2章 《二元一次方程组》章节检测卷
一、选择题(10小题,每小题3分,共30分)
1.下列方程中,属于二元一次方程的是( )
A. B. C.X+ =2 D.
2.用加减法解方程组,由②①消去未知数y,所得到的一元一次方程是( )
A. B. C. D.
3.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有人,物品的价格为钱,可列方程组为( )
A. B. C. D.
4.已知,用含x的代数式表示y可得( )
A. B. C. D.
5.如果表中给出的每一对,的值都是二元一次方程的解,则表中的值为( )
0 1 2 5
3 1
B. C.0 D.7
6.某校购买体育器材,第一次购买篮球7个,排球5个,足球3个,共花费450元,第二次又购买同样的篮球3个,排球2个,足球1个,共花费175元,则购买同样的篮球、排球、足球各1个,共需花费( )
A.100元 B.105元 C.110元 D.125元
7.已知关于x,y的方程组,若,则k的值为( )
A. B. C. D.
8.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2.图中各行从左到右列出的算筹数分别表示未知数的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是,在图2所示的算筹图中有一个图形被墨水覆盖了,如果图2所表示的方程组中的值为3,则被墨水所覆盖的图形为( )
A.| B.|| C.||| D.||||
9.已知关于x、y的二元一次方程组,给出下列结论:①当这个方程组的解x,y的值互为相反数时,;②当时,方程组的解也是方程的解;③无论取什么实数.的值始终不变;④若用表示,则.其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
10.有五张写有数字的卡片,分别记为①,②,③,④,⑤,将它们按如图所示放置在桌上.下表记录了相邻两张卡片上的数的和.
卡片编号 ①② ②③ ③④ ④⑤ ①⑤
两数的和
则写有最大数卡片的编号是( )
A.② B.③ C.④ D.⑤
二、填空题(6小题,每小题4分,共24分)
11.写出一个二元一次方程,使这个方程与所组成的方程组的解为,这个方程可以是 .
12.“鸡兔同笼”是我国古代的数学名题,《孙子算经》中这样叙述:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?若设雉只,兔只,则可列方程组为 .
13.已知关于的二元一次方程组的解为,小强因看错了系数,得到的解为,则 .
14.代数式(k≠0,且k、b为常数)的值随x取值的变化而变化,下表是当x取不同值时代数式对应的值,则关于x的方程的解为 .
x 0 4 8
4 6 8 10 12
15.对于实数,我们定义如下运算:若为非负数,则;若为负数,则.例如:,.则方程组的解为 .
16.某乐高创客小组自制了一台“滑轮塔吊”装置,如图,是平衡杆,点O处装有滑轮组,以的速度在平衡杆上滑动.现要将置于地面且距离障碍物的物体A搬运到障碍物后的置物台上,障碍物高为,置物台高为,两者宽度均为.在搬运过程中,滑轮滑动的同时,吊绳匀速收放.(物体体积、装置和滑轮组重力及摩擦力均忽略不计)
(1)物体在上升过程中,随着滑轮组向右滑动,吊绳匀速收起,若物体恰好能越过障碍物,则此时装置的收绳速度为 ;
(2)在(1)的基础上,物体缓缓上升,在到达某一高度后装置开始放绳,通过调整放绳速度,使物体顺利运至置物台.在搬运过程中,若物体恰好能以最小速度运至置物台,物体离地面最大高度为 .
三、解答题(8小题,共66分)
17.解方程组:
(1) (2)
18.已知关于、的二元一次方程组 的解为
(1)求,的值;
(2)求的立方根.
19.若等式 中的x,y满足方程组 ,求 的值.
20.已知关于x,y的方程组与有相同的解.
(1)求这个相同的解;
(2)求m、n的值;
(3)小明同学说:“无论a取何值,(1)中的解都是关于x,y的方程的解.”这句话对吗?请你说明理由.
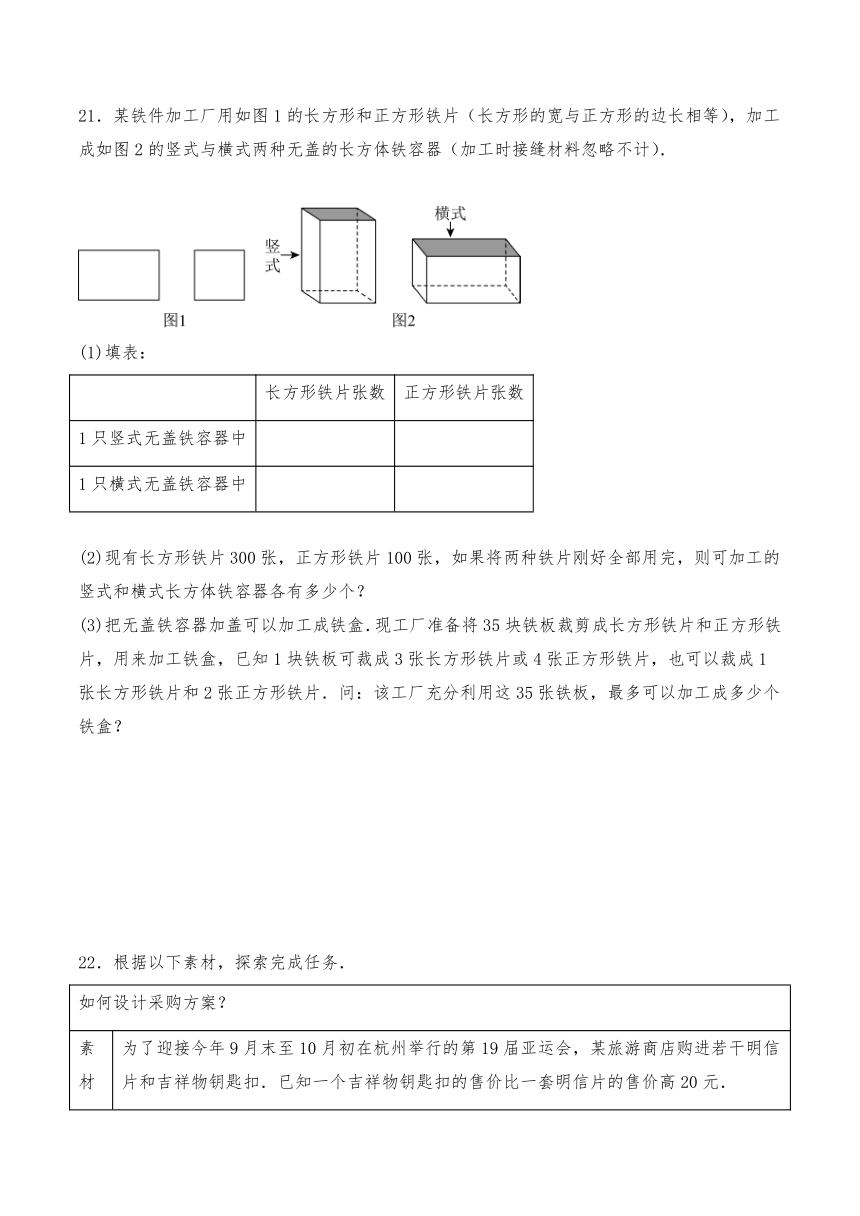
21.某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等),加工成如图2的竖式与横式两种无盖的长方体铁容器(加工时接缝材料忽略不计).
(1)填表:
长方形铁片张数 正方形铁片张数
1只竖式无盖铁容器中
1只横式无盖铁容器中
(2)现有长方形铁片300张,正方形铁片100张,如果将两种铁片刚好全部用完,则可加工的竖式和横式长方体铁容器各有多少个?
(3)把无盖铁容器加盖可以加工成铁盒.现工厂准备将35块铁板裁剪成长方形铁片和正方形铁片,用来加工铁盒,已知1块铁板可裁成3张长方形铁片或4张正方形铁片,也可以裁成1张长方形铁片和2张正方形铁片.问:该工厂充分利用这35张铁板,最多可以加工成多少个铁盒?
22.根据以下素材,探索完成任务.
如何设计采购方案?
素材1 为了迎接今年9月末至10月初在杭州举行的第19届亚运会,某旅游商店购进若干明信片和吉祥物钥匙扣.已知一个吉祥物钥匙扣的售价比一套明信片的售价高20元.
素材2 小明在本店购买了1套明信片与4个吉祥物钥匙扣与共花费130元.
素材3 已知明信片的进价为5元/套,吉祥物钥匙扣的进价为18元/个.为了促销,商店对吉祥物钥匙扣进行8折销售.临近期中考试,某老师打算提前给学生准备奖品,在本店同时购买吉祥物钥匙扣和明信片两种商品若干件,本次交易商家一共获得600元的销售额.
问题解决
任务1 假设明信片的售价为x元/套,钥匙扣的售价为y元/个,请协助解决右边问题. 问:___________(用含x的代数式表示)
任务2 基于任务1的假设和素材2的条件,请尝试求出吉祥物钥匙扣和明信片的售价.
任务3 【拟定设计方案】 请结合素材3中的信息,帮助该老师完成此次促销活动中可行的购买方案.在这些购买方案中,哪种方案商家获利最高.
23.对于关于x,y的二元一次方程组(其中,,,,,是常数),给出如下定义:若该方程组的解满足,则称这个方程组为“美好”方程组.
(1)下列方程组是“美好”方程组的是______(只填写序号);
①;②;③;④.
(2)若关于x,y的方程组是“美好”方程组,求a的值;
(3)若对于任意的有理数m,关于x,y的方程组都是“美好”方程组,求的值.
24.已知关于的方程组,其中,为整数.
(1)若方程组有无穷多组解,求实数与的值;
(2)当时,方程组是否有整数解?如有,求出整数解;若没有,请说明理由.
参考答案
一、选择题
1.B
【分析】本题考查二元一次方程,根据二元一次方程的定义判断即可.
【详解】解:根据二元一次方程的定义:方程中含有两个未知数,且含未知数的项的次数是1.可得:方程是二元一次方程.
故选:B
2.B
【分析】本题考查了加减法解一元二次方程,由②①即可求解;掌握解法是解题的关键.
【详解】解:②①得:
,
故选:B.
3.D
【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
根据题意可以找出题目中的等量关系,列出相应的方程组,从而可以解答本题.
【详解】解:由题意可得,
,
故选:D.
4.C
【分析】本题主要考查了解二元一次方程.根据已知条件,把含有x的项和常数项移到等号右边即可.
【详解】解:∵,
∴,
故选:C.
5.A
【分析】本题考查了二元一次方程的解,能熟记方程的解的定义(使方程左右两边相等的未知数的值,叫方程的解)是解此题的关键.
将代入中求出,再把代入求出,再将代入方程即可求出m.
【详解】解:把代入,得,
∴,
则,
把代入,得,
∴,
∴二元一次方程为:,
把代入,得,
∴,
∴.
故选:A.
6.A
7.A
【分析】本题考查了二元一次方程组的特殊解法,解一元一次方程,熟练掌握方程组的解法是解题关键.先利用方程组中的第二个方程减去第一个方程得,再根据得到的一元一次方程,解方程即可.
【详解】解:
由得,,即
解得:.
故选:A.
8.B
【分析】本题主要考查了二元一次方程组的应用.设被墨水所覆盖的图形表示的数据为,根据题意列出方程组,把代入,求得的值便可.
【详解】解:设被墨水所覆盖的图形表示的数据为,根据题意得,
,
把代入,得
由③得,,
把代入④得,,
,
故选:B.
9.C
【分析】本题考查二元一次方程组的解法和应用,正确的解出方程组的解是解决问题的关键.根据方程组的解法可以得到,①令,即可求出a的值,验证即可;②由①得,而,将代入验证得出答案;③根据方程组的解得到,即可判断;④用含有x的代数式表示a,代入得出x、y的关系.
【详解】解:①,
解得:,
∵x,y的值互为相反数,
∴,
解得:,故正确;
②原方程组的解满足,
当时,,
而方程的解不满足,故错误;
③∵,
∴,
即的值始终不变,故正确;
④∵,
∴,代入,
得:,即,故正确;
故选:C.
10.A
【分析】本题考查了等式的性质,由题意得关于①②③④⑤的方程,利用等式的性质求出它们的值,最后根据题意得结论.
【详解】解:①②,②③,③④,④⑤,①⑤ ,
,得③①,,得⑤③ .
,得⑤①.
,得⑤,,得①.
⑤,①.
把⑤①的值代入、、、得②,③,④.
故选:A.
二、填空题
11.(答案不唯一)
【分析】本题考查二元一次方程的定义及二元一次方程组解的定义,
根据二元一次方程的解的定义求得的值,然后写出一个符合题意的方程即可.
【详解】解:∵的一组解为,
∴,
解得:,
则它的解为,
那么所组成的方程组的解为的二元一次方程为,
故答案为:(答案不唯一).
12.
【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,找出等量关系,列出相应的方程组.根据“雉的数量兔的数量,雉的脚的数量兔子的脚的数量”可列方程组.
【详解】解:根据题意可得:,
故答案为:.
13.
【分析】本题考查了二元一次方程组的解.根据题意把代入二元一次方程组可得的值,根据小强看错系数得到解为,由此可得新的方程组,运用加减消元法可求出的值,代入计算即可求解.
【详解】解:把代入二元一次方程组得,
,
∴由得,,
∵小强看错了系数得到,
∴,
∴,
①②得,,
解得,,
把代入②得,,
解得,,
∴,
故答案为:11.
14.
【分析】本题考查解方程和方程组.根据表中和,得到关于和的二元一次方程并求解,将和的值代入解方程即可.
【详解】解:由和,
得,
解得,
将代入,
解得,
故答案为:.
15.或
【分析】此题考查了解二元一次方程组,实数的新定义运算,分类讨论与分别为非负数和负数四种情况考虑,方程组利用题中的新定义化简求出与的值,即可作出判断.
【详解】解:当,,即,时,
解得:
当,,即,时,
解得:,
当,,即,时,
解得: (舍去)
当,,即,时,
解得:(舍去)
综上所述,或
故答案为:或.
16. 3 50
【分析】本题考查了有理数的加减法、除法,以及二元一次方程组,熟练掌握知识点,正确理解题意是解题的关键.
(1)根据题意得滑轮组向右滑动的距离为,时间为秒,吊绳匀速收起,障碍物高为,故装置的收绳速度为:;
(2)设从点A到最高点的时间为,则,设为两个矩形的顶点,由题意得,只有贴着障碍物右侧P点滑下来,滑到平台的最右侧Q点,物体恰好能以最小速度运至置物台,从点P到点Q分析,水平方向是匀速的,即,从点P到点Q,即水平方向从点C到点E,距离为,则时间为,而竖直方向的时间也为,点P与点Q的竖直高度差为,故从点P到点Q的竖直速度为,设从点F到点Q的时间为,则竖直下落的高度,由,而水平方向从点A到点E的距离为,,故,可得,解得:,故.
【详解】解:(1)根据题意得滑轮组向右滑动的距离为,
时间为秒,
吊绳匀速收起,障碍物高为,
∴装置的收绳速度为:,
故答案为:3;
(2)由(1),设从点A到最高点的时间为,则,如图:
设为两个矩形的顶点,由题意得,只有贴着障碍物右侧P点滑下来,滑到平台的最右侧Q点,物体恰好能以最小速度运至置物台,
∵从点P到点Q分析,水平方向是匀速的,即,从点P到点Q,即水平方向从点C到点E,距离为,则时间为,而竖直方向的时间也为,
∵点P与点Q的竖直高度差为,
∴从点P到点Q的竖直速度为,
设从点F到点Q的时间为,
∴竖直下落的高度,
∵,
∵水平方向从点A到点E的距离为,
∴,
∴,
解得:,
∴,
故答案为:50.
三、解答题
17.(1)解:,
得,
解得,
将代入得,
解得,
∴方程组的解为:;
(2)解:,
原方程组化简为:,
得:,
解得,
将代入得,
解得,
∴方程组的解为:.
18.(1)解:根据题意得:,
解得:,
,;
(2),,
,
的立方根为.
19.解:∵
∴
解得
将 代入方程组 得 解得
∴原式
20.(1)解:由题意可得:,
解得;
(2)解:将代入含有m、n的方程得:,
解得:;
(3)解:将代入,得:
,
化简得:,
该说法错误.
21.(1)解:根据图2可知:1只竖式无盖铁容器中长方形铁片4张,正方形铁片1张;1只横式无盖铁容器中长方形铁片3张,正方形铁片2张;
填表:
长方形铁片张数 正方形铁片张数
1只竖式无盖铁容器中 4 1
1只横式无盖铁容器中 3 2
(2)解:设可以加工竖式长方体铁容器x个,横式长方体铁容器y个,
依题意,得:,
解得:.
答:可以加工竖式长方体铁容器60个,横式长方体铁容器20个.
(3)解:设用m块铁板裁成长方形铁片,n块铁板裁成正方形铁片,则用块铁板裁成长方形铁片和正方形铁片,依题意,得:
,
∴,
∵m,n,均为非负整数,
∴或,
当,时,;
当,时,;
∵,
∴最多可以加工成19个铁盒.
22.解:任务1:
由题意可知,一个吉祥物钥匙扣的售价比一套明信片的售价高20元,
设明信片的售价为x元/套,钥匙扣的售价为y元/个,
则,
故答案为:;
任务2:
∵小明在本店购买了1套明信片与4个吉祥物钥匙扣与共花费130元,
,
解得,
,
答:吉祥物钥匙扣的售价为30元,明信片的售价为10元;
任务3:
设购买吉祥物钥匙扣m个,明信片n张,
根据题意得:,
,
是非负整数,
或或或或或,
∵吉祥物钥匙扣每件利润为(元),明信片每张利润为(元),
∴购买吉祥物钥匙扣0个,明信片60张,商家获利300元;
购买吉祥物钥匙扣5个,明信片48张,商家获利270元;
购买吉祥物钥匙扣10个,明信片36张,商家获利240元;
购买吉祥物钥匙扣15个,明信片24张,商家获利210元;
购买吉祥物钥匙扣20个,明信片12张,商家获利180元;
购买吉祥物钥匙扣25个,明信片0张,商家获利150元;
答:可行的购买方案有:购买吉祥物钥匙扣0个,明信片60张或购买吉祥物钥匙扣5个,明信片48张,或购买吉祥物钥匙扣10个,明信片36张或购买吉祥物钥匙扣15个,明信片24张或购买吉祥物钥匙扣20个,明信片12张或购买吉祥物钥匙扣25个,明信片0张;其中购买吉祥物钥匙扣0个,明信片60张商家获利最高.
23.(1)解:①,解得:,此时;
②,解得:,此时;
③,解得:,此时;
④,解得:,此时;
故答案为:②③;
(2)解:,
由得:,
解得:,
把代入①得:,
解得:,
∵关于x,y的方程组是“美好”方程组,
∴,
∴,
解得:;
(3)解:∵关于x,y的方程组都是“美好”方程组,
∴,
联立得:,
解得:或,
把代入得:
,
∴,
∵m为任意有理数,
∴,解得:,
∴;
把代入得:
,
∴,
∵m为任意有理数,
∴,解得:,
∴;
综上所述,得值为或.
24.(1)解:依题意,
由①得,,③
将③代入②得,
整理得出,④
∵方程组有无穷多组解
∴且时,
即,则,
∴,
(2)解:没有,理由如下:
由(1)得
∵
∴
整理得
①当时,即,
∵
∴此时方程组为
则
∵为整数
∴原方程没有整数解
②当时,即,此时,
若时,显然无解,
若时,,代入得
∵a为整数,
∴不可能为整数,
∴原方程无整数解;
综上:原方程没有整数解
一、选择题(10小题,每小题3分,共30分)
1.下列方程中,属于二元一次方程的是( )
A. B. C.X+ =2 D.
2.用加减法解方程组,由②①消去未知数y,所得到的一元一次方程是( )
A. B. C. D.
3.我国古代数学名著《九章算术》中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”大意是:现在有数人一起去买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问共有多少人,物品的价格是多少钱?若设人数共有人,物品的价格为钱,可列方程组为( )
A. B. C. D.
4.已知,用含x的代数式表示y可得( )
A. B. C. D.
5.如果表中给出的每一对,的值都是二元一次方程的解,则表中的值为( )
0 1 2 5
3 1
B. C.0 D.7
6.某校购买体育器材,第一次购买篮球7个,排球5个,足球3个,共花费450元,第二次又购买同样的篮球3个,排球2个,足球1个,共花费175元,则购买同样的篮球、排球、足球各1个,共需花费( )
A.100元 B.105元 C.110元 D.125元
7.已知关于x,y的方程组,若,则k的值为( )
A. B. C. D.
8.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2.图中各行从左到右列出的算筹数分别表示未知数的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是,在图2所示的算筹图中有一个图形被墨水覆盖了,如果图2所表示的方程组中的值为3,则被墨水所覆盖的图形为( )
A.| B.|| C.||| D.||||
9.已知关于x、y的二元一次方程组,给出下列结论:①当这个方程组的解x,y的值互为相反数时,;②当时,方程组的解也是方程的解;③无论取什么实数.的值始终不变;④若用表示,则.其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.②③④
10.有五张写有数字的卡片,分别记为①,②,③,④,⑤,将它们按如图所示放置在桌上.下表记录了相邻两张卡片上的数的和.
卡片编号 ①② ②③ ③④ ④⑤ ①⑤
两数的和
则写有最大数卡片的编号是( )
A.② B.③ C.④ D.⑤
二、填空题(6小题,每小题4分,共24分)
11.写出一个二元一次方程,使这个方程与所组成的方程组的解为,这个方程可以是 .
12.“鸡兔同笼”是我国古代的数学名题,《孙子算经》中这样叙述:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?若设雉只,兔只,则可列方程组为 .
13.已知关于的二元一次方程组的解为,小强因看错了系数,得到的解为,则 .
14.代数式(k≠0,且k、b为常数)的值随x取值的变化而变化,下表是当x取不同值时代数式对应的值,则关于x的方程的解为 .
x 0 4 8
4 6 8 10 12
15.对于实数,我们定义如下运算:若为非负数,则;若为负数,则.例如:,.则方程组的解为 .
16.某乐高创客小组自制了一台“滑轮塔吊”装置,如图,是平衡杆,点O处装有滑轮组,以的速度在平衡杆上滑动.现要将置于地面且距离障碍物的物体A搬运到障碍物后的置物台上,障碍物高为,置物台高为,两者宽度均为.在搬运过程中,滑轮滑动的同时,吊绳匀速收放.(物体体积、装置和滑轮组重力及摩擦力均忽略不计)
(1)物体在上升过程中,随着滑轮组向右滑动,吊绳匀速收起,若物体恰好能越过障碍物,则此时装置的收绳速度为 ;
(2)在(1)的基础上,物体缓缓上升,在到达某一高度后装置开始放绳,通过调整放绳速度,使物体顺利运至置物台.在搬运过程中,若物体恰好能以最小速度运至置物台,物体离地面最大高度为 .
三、解答题(8小题,共66分)
17.解方程组:
(1) (2)
18.已知关于、的二元一次方程组 的解为
(1)求,的值;
(2)求的立方根.
19.若等式 中的x,y满足方程组 ,求 的值.
20.已知关于x,y的方程组与有相同的解.
(1)求这个相同的解;
(2)求m、n的值;
(3)小明同学说:“无论a取何值,(1)中的解都是关于x,y的方程的解.”这句话对吗?请你说明理由.
21.某铁件加工厂用如图1的长方形和正方形铁片(长方形的宽与正方形的边长相等),加工成如图2的竖式与横式两种无盖的长方体铁容器(加工时接缝材料忽略不计).
(1)填表:
长方形铁片张数 正方形铁片张数
1只竖式无盖铁容器中
1只横式无盖铁容器中
(2)现有长方形铁片300张,正方形铁片100张,如果将两种铁片刚好全部用完,则可加工的竖式和横式长方体铁容器各有多少个?
(3)把无盖铁容器加盖可以加工成铁盒.现工厂准备将35块铁板裁剪成长方形铁片和正方形铁片,用来加工铁盒,已知1块铁板可裁成3张长方形铁片或4张正方形铁片,也可以裁成1张长方形铁片和2张正方形铁片.问:该工厂充分利用这35张铁板,最多可以加工成多少个铁盒?
22.根据以下素材,探索完成任务.
如何设计采购方案?
素材1 为了迎接今年9月末至10月初在杭州举行的第19届亚运会,某旅游商店购进若干明信片和吉祥物钥匙扣.已知一个吉祥物钥匙扣的售价比一套明信片的售价高20元.
素材2 小明在本店购买了1套明信片与4个吉祥物钥匙扣与共花费130元.
素材3 已知明信片的进价为5元/套,吉祥物钥匙扣的进价为18元/个.为了促销,商店对吉祥物钥匙扣进行8折销售.临近期中考试,某老师打算提前给学生准备奖品,在本店同时购买吉祥物钥匙扣和明信片两种商品若干件,本次交易商家一共获得600元的销售额.
问题解决
任务1 假设明信片的售价为x元/套,钥匙扣的售价为y元/个,请协助解决右边问题. 问:___________(用含x的代数式表示)
任务2 基于任务1的假设和素材2的条件,请尝试求出吉祥物钥匙扣和明信片的售价.
任务3 【拟定设计方案】 请结合素材3中的信息,帮助该老师完成此次促销活动中可行的购买方案.在这些购买方案中,哪种方案商家获利最高.
23.对于关于x,y的二元一次方程组(其中,,,,,是常数),给出如下定义:若该方程组的解满足,则称这个方程组为“美好”方程组.
(1)下列方程组是“美好”方程组的是______(只填写序号);
①;②;③;④.
(2)若关于x,y的方程组是“美好”方程组,求a的值;
(3)若对于任意的有理数m,关于x,y的方程组都是“美好”方程组,求的值.
24.已知关于的方程组,其中,为整数.
(1)若方程组有无穷多组解,求实数与的值;
(2)当时,方程组是否有整数解?如有,求出整数解;若没有,请说明理由.
参考答案
一、选择题
1.B
【分析】本题考查二元一次方程,根据二元一次方程的定义判断即可.
【详解】解:根据二元一次方程的定义:方程中含有两个未知数,且含未知数的项的次数是1.可得:方程是二元一次方程.
故选:B
2.B
【分析】本题考查了加减法解一元二次方程,由②①即可求解;掌握解法是解题的关键.
【详解】解:②①得:
,
故选:B.
3.D
【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,列出相应的方程组.
根据题意可以找出题目中的等量关系,列出相应的方程组,从而可以解答本题.
【详解】解:由题意可得,
,
故选:D.
4.C
【分析】本题主要考查了解二元一次方程.根据已知条件,把含有x的项和常数项移到等号右边即可.
【详解】解:∵,
∴,
故选:C.
5.A
【分析】本题考查了二元一次方程的解,能熟记方程的解的定义(使方程左右两边相等的未知数的值,叫方程的解)是解此题的关键.
将代入中求出,再把代入求出,再将代入方程即可求出m.
【详解】解:把代入,得,
∴,
则,
把代入,得,
∴,
∴二元一次方程为:,
把代入,得,
∴,
∴.
故选:A.
6.A
7.A
【分析】本题考查了二元一次方程组的特殊解法,解一元一次方程,熟练掌握方程组的解法是解题关键.先利用方程组中的第二个方程减去第一个方程得,再根据得到的一元一次方程,解方程即可.
【详解】解:
由得,,即
解得:.
故选:A.
8.B
【分析】本题主要考查了二元一次方程组的应用.设被墨水所覆盖的图形表示的数据为,根据题意列出方程组,把代入,求得的值便可.
【详解】解:设被墨水所覆盖的图形表示的数据为,根据题意得,
,
把代入,得
由③得,,
把代入④得,,
,
故选:B.
9.C
【分析】本题考查二元一次方程组的解法和应用,正确的解出方程组的解是解决问题的关键.根据方程组的解法可以得到,①令,即可求出a的值,验证即可;②由①得,而,将代入验证得出答案;③根据方程组的解得到,即可判断;④用含有x的代数式表示a,代入得出x、y的关系.
【详解】解:①,
解得:,
∵x,y的值互为相反数,
∴,
解得:,故正确;
②原方程组的解满足,
当时,,
而方程的解不满足,故错误;
③∵,
∴,
即的值始终不变,故正确;
④∵,
∴,代入,
得:,即,故正确;
故选:C.
10.A
【分析】本题考查了等式的性质,由题意得关于①②③④⑤的方程,利用等式的性质求出它们的值,最后根据题意得结论.
【详解】解:①②,②③,③④,④⑤,①⑤ ,
,得③①,,得⑤③ .
,得⑤①.
,得⑤,,得①.
⑤,①.
把⑤①的值代入、、、得②,③,④.
故选:A.
二、填空题
11.(答案不唯一)
【分析】本题考查二元一次方程的定义及二元一次方程组解的定义,
根据二元一次方程的解的定义求得的值,然后写出一个符合题意的方程即可.
【详解】解:∵的一组解为,
∴,
解得:,
则它的解为,
那么所组成的方程组的解为的二元一次方程为,
故答案为:(答案不唯一).
12.
【分析】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,找出等量关系,列出相应的方程组.根据“雉的数量兔的数量,雉的脚的数量兔子的脚的数量”可列方程组.
【详解】解:根据题意可得:,
故答案为:.
13.
【分析】本题考查了二元一次方程组的解.根据题意把代入二元一次方程组可得的值,根据小强看错系数得到解为,由此可得新的方程组,运用加减消元法可求出的值,代入计算即可求解.
【详解】解:把代入二元一次方程组得,
,
∴由得,,
∵小强看错了系数得到,
∴,
∴,
①②得,,
解得,,
把代入②得,,
解得,,
∴,
故答案为:11.
14.
【分析】本题考查解方程和方程组.根据表中和,得到关于和的二元一次方程并求解,将和的值代入解方程即可.
【详解】解:由和,
得,
解得,
将代入,
解得,
故答案为:.
15.或
【分析】此题考查了解二元一次方程组,实数的新定义运算,分类讨论与分别为非负数和负数四种情况考虑,方程组利用题中的新定义化简求出与的值,即可作出判断.
【详解】解:当,,即,时,
解得:
当,,即,时,
解得:,
当,,即,时,
解得: (舍去)
当,,即,时,
解得:(舍去)
综上所述,或
故答案为:或.
16. 3 50
【分析】本题考查了有理数的加减法、除法,以及二元一次方程组,熟练掌握知识点,正确理解题意是解题的关键.
(1)根据题意得滑轮组向右滑动的距离为,时间为秒,吊绳匀速收起,障碍物高为,故装置的收绳速度为:;
(2)设从点A到最高点的时间为,则,设为两个矩形的顶点,由题意得,只有贴着障碍物右侧P点滑下来,滑到平台的最右侧Q点,物体恰好能以最小速度运至置物台,从点P到点Q分析,水平方向是匀速的,即,从点P到点Q,即水平方向从点C到点E,距离为,则时间为,而竖直方向的时间也为,点P与点Q的竖直高度差为,故从点P到点Q的竖直速度为,设从点F到点Q的时间为,则竖直下落的高度,由,而水平方向从点A到点E的距离为,,故,可得,解得:,故.
【详解】解:(1)根据题意得滑轮组向右滑动的距离为,
时间为秒,
吊绳匀速收起,障碍物高为,
∴装置的收绳速度为:,
故答案为:3;
(2)由(1),设从点A到最高点的时间为,则,如图:
设为两个矩形的顶点,由题意得,只有贴着障碍物右侧P点滑下来,滑到平台的最右侧Q点,物体恰好能以最小速度运至置物台,
∵从点P到点Q分析,水平方向是匀速的,即,从点P到点Q,即水平方向从点C到点E,距离为,则时间为,而竖直方向的时间也为,
∵点P与点Q的竖直高度差为,
∴从点P到点Q的竖直速度为,
设从点F到点Q的时间为,
∴竖直下落的高度,
∵,
∵水平方向从点A到点E的距离为,
∴,
∴,
解得:,
∴,
故答案为:50.
三、解答题
17.(1)解:,
得,
解得,
将代入得,
解得,
∴方程组的解为:;
(2)解:,
原方程组化简为:,
得:,
解得,
将代入得,
解得,
∴方程组的解为:.
18.(1)解:根据题意得:,
解得:,
,;
(2),,
,
的立方根为.
19.解:∵
∴
解得
将 代入方程组 得 解得
∴原式
20.(1)解:由题意可得:,
解得;
(2)解:将代入含有m、n的方程得:,
解得:;
(3)解:将代入,得:
,
化简得:,
该说法错误.
21.(1)解:根据图2可知:1只竖式无盖铁容器中长方形铁片4张,正方形铁片1张;1只横式无盖铁容器中长方形铁片3张,正方形铁片2张;
填表:
长方形铁片张数 正方形铁片张数
1只竖式无盖铁容器中 4 1
1只横式无盖铁容器中 3 2
(2)解:设可以加工竖式长方体铁容器x个,横式长方体铁容器y个,
依题意,得:,
解得:.
答:可以加工竖式长方体铁容器60个,横式长方体铁容器20个.
(3)解:设用m块铁板裁成长方形铁片,n块铁板裁成正方形铁片,则用块铁板裁成长方形铁片和正方形铁片,依题意,得:
,
∴,
∵m,n,均为非负整数,
∴或,
当,时,;
当,时,;
∵,
∴最多可以加工成19个铁盒.
22.解:任务1:
由题意可知,一个吉祥物钥匙扣的售价比一套明信片的售价高20元,
设明信片的售价为x元/套,钥匙扣的售价为y元/个,
则,
故答案为:;
任务2:
∵小明在本店购买了1套明信片与4个吉祥物钥匙扣与共花费130元,
,
解得,
,
答:吉祥物钥匙扣的售价为30元,明信片的售价为10元;
任务3:
设购买吉祥物钥匙扣m个,明信片n张,
根据题意得:,
,
是非负整数,
或或或或或,
∵吉祥物钥匙扣每件利润为(元),明信片每张利润为(元),
∴购买吉祥物钥匙扣0个,明信片60张,商家获利300元;
购买吉祥物钥匙扣5个,明信片48张,商家获利270元;
购买吉祥物钥匙扣10个,明信片36张,商家获利240元;
购买吉祥物钥匙扣15个,明信片24张,商家获利210元;
购买吉祥物钥匙扣20个,明信片12张,商家获利180元;
购买吉祥物钥匙扣25个,明信片0张,商家获利150元;
答:可行的购买方案有:购买吉祥物钥匙扣0个,明信片60张或购买吉祥物钥匙扣5个,明信片48张,或购买吉祥物钥匙扣10个,明信片36张或购买吉祥物钥匙扣15个,明信片24张或购买吉祥物钥匙扣20个,明信片12张或购买吉祥物钥匙扣25个,明信片0张;其中购买吉祥物钥匙扣0个,明信片60张商家获利最高.
23.(1)解:①,解得:,此时;
②,解得:,此时;
③,解得:,此时;
④,解得:,此时;
故答案为:②③;
(2)解:,
由得:,
解得:,
把代入①得:,
解得:,
∵关于x,y的方程组是“美好”方程组,
∴,
∴,
解得:;
(3)解:∵关于x,y的方程组都是“美好”方程组,
∴,
联立得:,
解得:或,
把代入得:
,
∴,
∵m为任意有理数,
∴,解得:,
∴;
把代入得:
,
∴,
∵m为任意有理数,
∴,解得:,
∴;
综上所述,得值为或.
24.(1)解:依题意,
由①得,,③
将③代入②得,
整理得出,④
∵方程组有无穷多组解
∴且时,
即,则,
∴,
(2)解:没有,理由如下:
由(1)得
∵
∴
整理得
①当时,即,
∵
∴此时方程组为
则
∵为整数
∴原方程没有整数解
②当时,即,此时,
若时,显然无解,
若时,,代入得
∵a为整数,
∴不可能为整数,
∴原方程无整数解;
综上:原方程没有整数解
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
