七年级数学下册浙教版 1.4《平行线的判定》小节复习题(含答案)
文档属性
| 名称 | 七年级数学下册浙教版 1.4《平行线的判定》小节复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 21:14:52 | ||
图片预览

文档简介
1.4《平行线的判定》小节复习题
题型01 同位角相等两直线平行
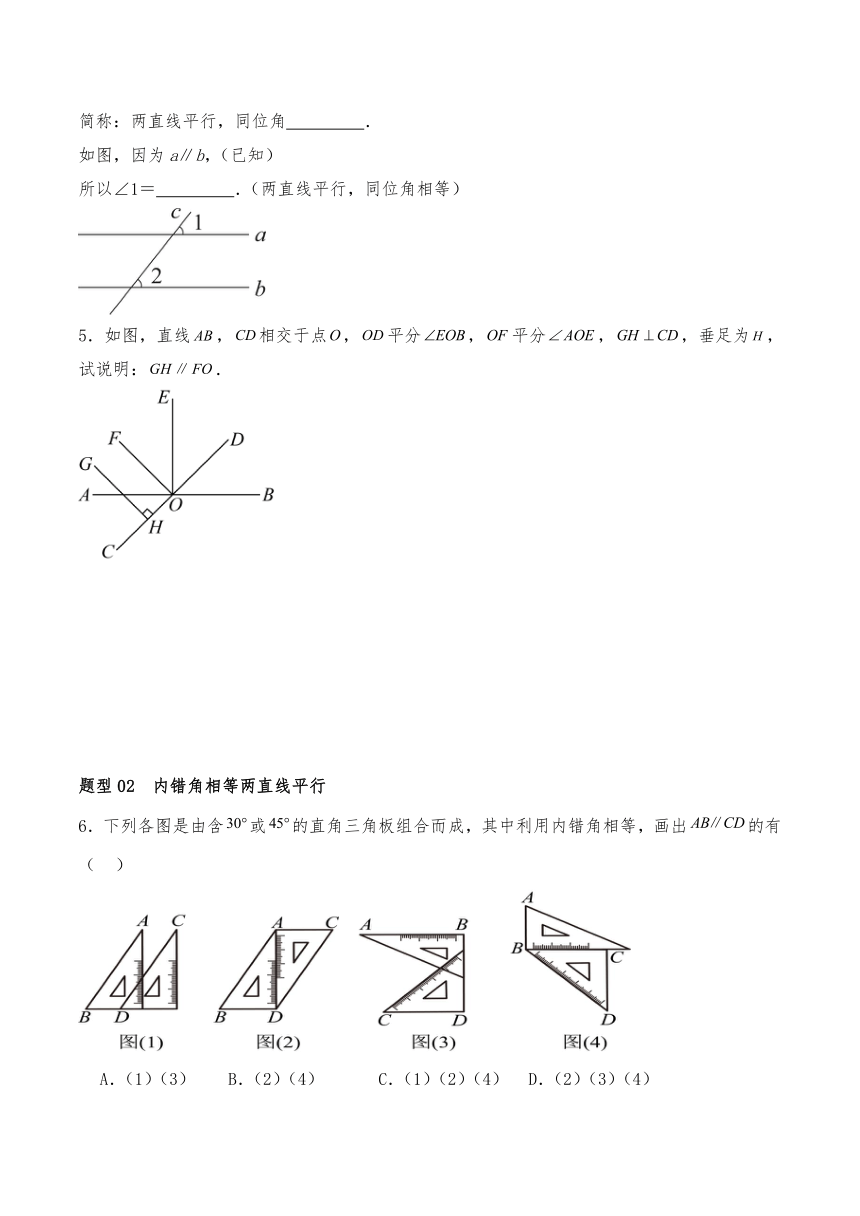
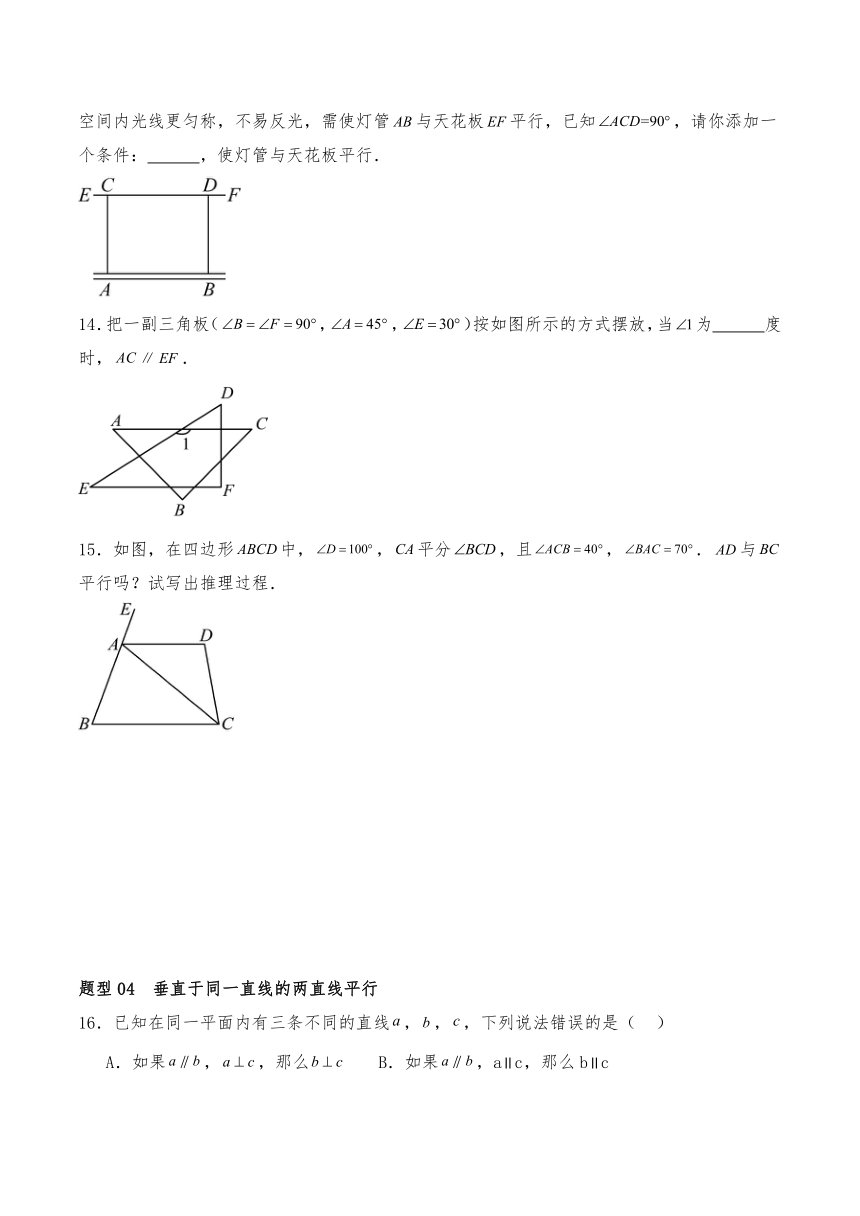
1.如图,木工师傅用图中的角尺画平行线的依据是( )
A.同位角相等,两直线平行
B.平行于同一条直线的两条直线平行
C.经过直线外一点,有且只有一条直线与这条直线平行两直线平行,同位角相等
D.两直线平行,同位角相等
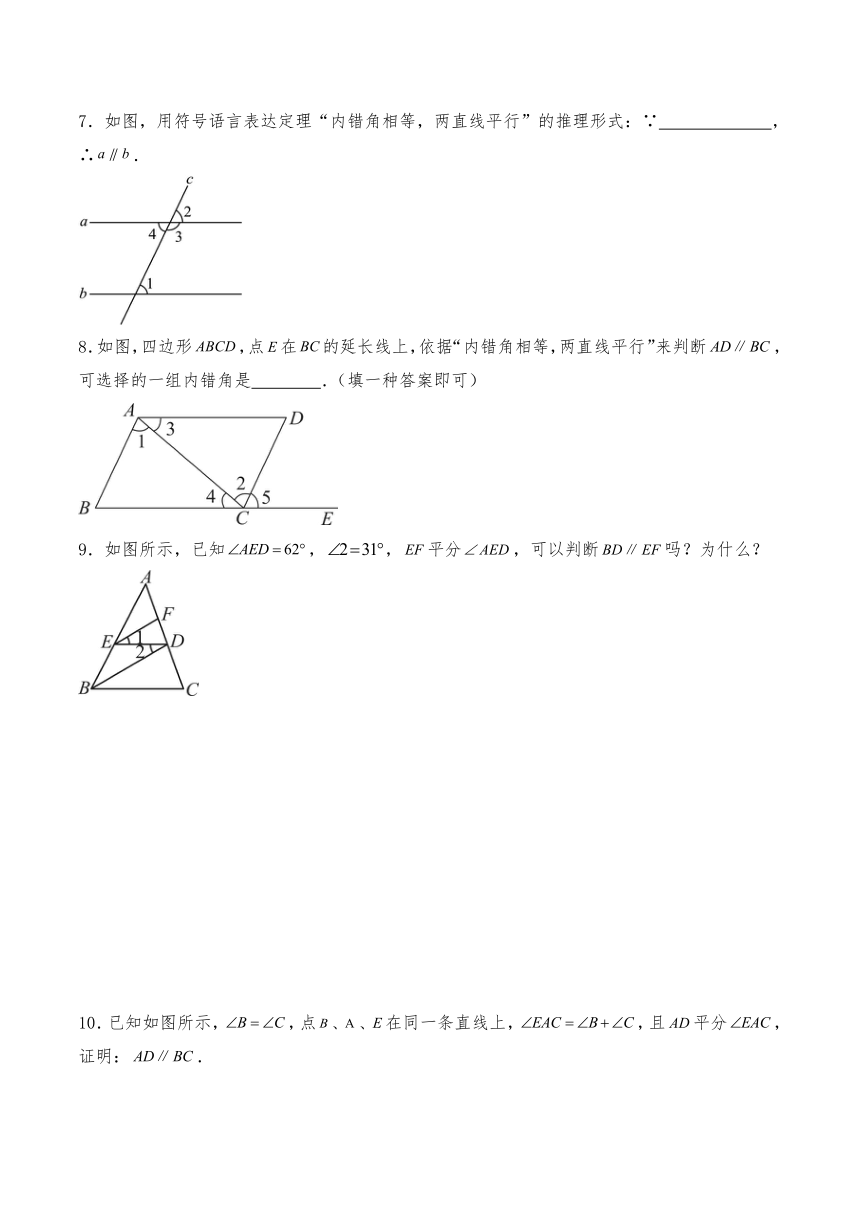
2.下列各图中,的依据是“同位角相等,两直线平行”的是( )
A.①③ B.①②④ C.③④ D.①②③④
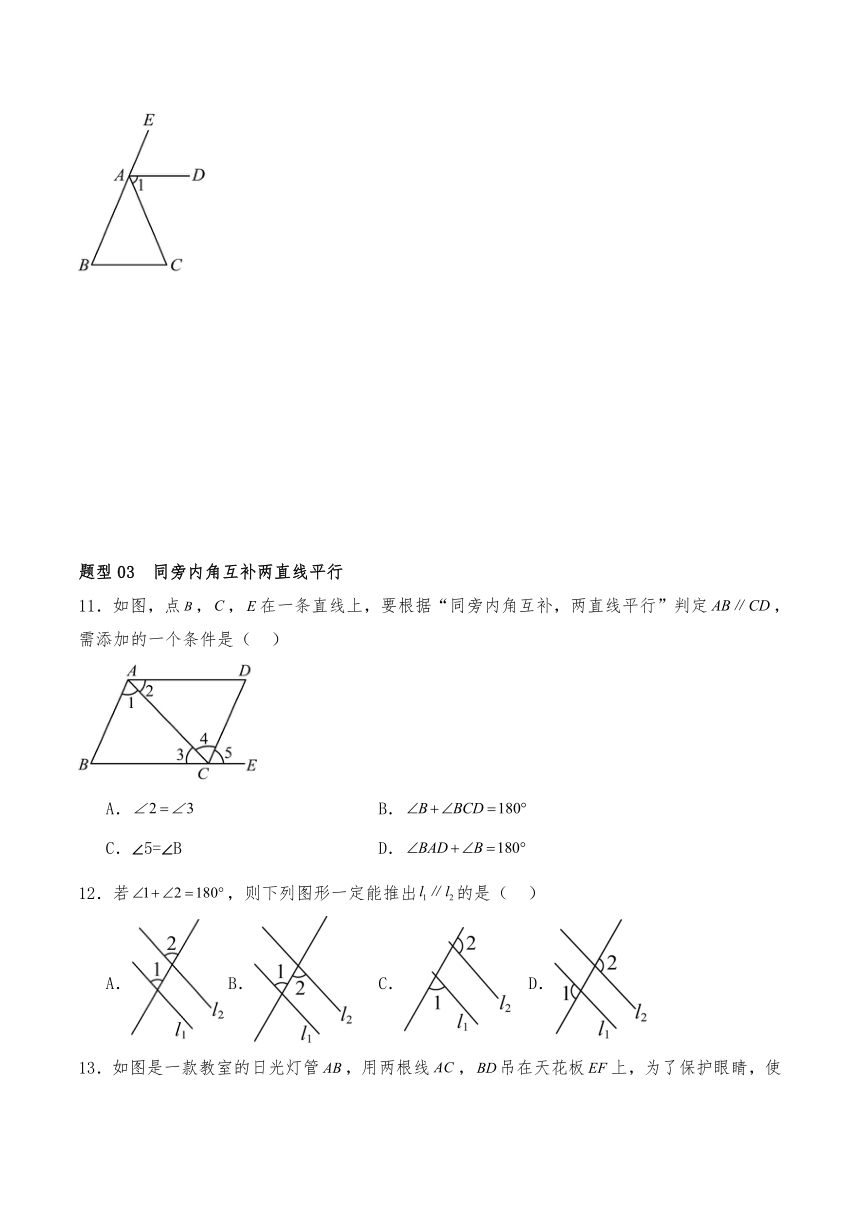
3.结合下图,用符号语言表达定理“同位角相等,两直线平行”的推理形式:∵ ,∴.
4.两条平行直线被第三条直线所截,同位角相等.
简称:两直线平行,同位角 .
如图,因为a∥b,(已知)
所以∠1= .(两直线平行,同位角相等)
5.如图,直线,相交于点,平分,平分,,垂足为,试说明:.
题型02 内错角相等两直线平行
6.下列各图是由含或的直角三角板组合而成,其中利用内错角相等,画出的有( )
A.(1)(3) B.(2)(4) C.(1)(2)(4) D.(2)(3)(4)
7.如图,用符号语言表达定理“内错角相等,两直线平行”的推理形式:∵ ,∴.
8.如图,四边形,点在的延长线上,依据“内错角相等,两直线平行”来判断,可选择的一组内错角是 .(填一种答案即可)
9.如图所示,已知,,平分,可以判断吗?为什么?
10.已知如图所示,,点、、在同一条直线上,,且平分,证明:.
题型03 同旁内角互补两直线平行
11.如图,点,,在一条直线上,要根据“同旁内角互补,两直线平行”判定,需添加的一个条件是( )
A. B.
C.∠5=∠B D.
12.若,则下列图形一定能推出的是( )
A. B. C. D.
13.如图是一款教室的日光灯管,用两根线,吊在天花板上,为了保护眼睛,使空间内光线更匀称,不易反光,需使灯管与天花板平行,已知,请你添加一个条件: ,使灯管与天花板平行.
14.把一副三角板(,,)按如图所示的方式摆放,当为 度时,.
15.如图,在四边形中,,平分,且,.与平行吗?试写出推理过程.
题型04 垂直于同一直线的两直线平行
16.已知在同一平面内有三条不同的直线,,,下列说法错误的是( )
A.如果,,那么 B.如果,a∥c,那么b∥c
C.如果a⊥b,,那么 D.如果a⊥b,,那么b∥c
17.a,b,c为平面内不同的三条直线,若要,条件不符合的是( )
A., B.a⊥b,
C., D.c截a,b所得的内错角的邻补角相等
18.下列命题中的真命题是( )
A.若,,则 B.若a⊥b,,则
C.若a⊥b,,则 D.若a⊥b,,则
19.在同一平面内有2021条直线a1,a2,a3,…,a2021,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a5的位置关系是 ;a1与a2021的位置关系是 .
20.对于同一平面内三条直线、、有以下论断:
①;②;③;④;⑤.
请以其中两个论断为条件,一个论断为结论,组成一个真命题.
题型05 平行线判定方法的结合问题
21.如图,下列能判定的条件的个数是( )
①;②;③;④
A.1个 B.2个 C.3个 D.4个
22.如图,点在的延长线上,下列条件中不能判断的是( )
A. B.
C. D.
23.如图,点在的延长线上,给出下列条件:
①;②;③;④,⑤,⑥
一定能判定的条件有( )
A.个 B.个 C.个 D.个
24.如图,直线a、b都与直线c相交,给出下列条件:①;②;③;④.其中能判断的条件是( )
A.①② B.③④ C.①③④ D.①②③
25.如图,点E在的延长线上,给出下列条件:
(1);(2);(3);(4);(5);(6),能判断出的条件有 .(填序号)
题型06 平行线的判定(填空型大题)
26.请完善下列题目的解答过程,并在括号内填写相应的理论依据.
已知:如图,,且,求证:.
解:∵,,
∴( )
∴,,
又∵(已知)
∴______=______( )
∴( )
27.如图1,在数学活动课上,同学们探究过直线外一点P画的方法,其中王玲是通过折纸的方式完成:
第一步:如图2,过点P进行第一次折叠,使点B的对称点B 落在上,折痕与相交于点Q,打开纸张铺平;
第二步:如图3,过点P进行第二次折叠,使折痕,打开纸张铺平(如图4);
王玲就说,你能用几何推理说说其中的道理吗?
(请完成下面的证明,并填上对应的推理根据)
证明:∵∠AQB=180°
∴∠ ∠AQB= .理由是:(角平分线的定义).
∵,
∴∠ .理由是:( ).
∴ ,
∴.理由是:( ).
28.完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( )
∵平分(已知),
∴_________( )
∴( )
∵(已知),
∴_________( )
∴( )
29.完成下面推理及填空:
已知:如图,在 ABC中,于点是上一点,且,求证:.
证明:(已知).
_______( )
______.
.( ).
______(______).
∴______( ).
30.完成下面的证明:
已知:如图,,,.求证:.
证明:(________)
________(________)
,(已知)
________
即________
(________)
题型07 平行线的判定综合
31.如图,已知平分,平分,且.
(1)与平行吗? 为什么?
(2)请判断与的位置关系,并说明理由.
32.如图,,,.
(1)与有怎样的位置关系?为什么?
(2)与平行吗?若平行,请说明理由;若不平行,那么再加上什么条件就平行了呢?
33.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
34.如图,台球运动中母球击中桌边的点,经桌边反弹后击中相邻的另一桌边的点,再次反弹经过点,其中,.
(1)若∠PAD=32°,求的度数;
(2)已知,求证:.
35.如图,直线与直线,分别相交于点M,O,,分别平分和,与交于点P,Q,已知.
(1)若,求的度数;
(2)对说明理由.
参考答案
题型01 同位角相等两直线平行
1.A
【分析】本题考查了平行线的判定.解题的关键在于对知识的熟练掌握与灵活运用.根据平行线的判定进行解答即可.
【详解】解:由题意知,木工用图中的角尺画平行线的依据是:同位角相等,两直线平行,
故选:A.
2.A
【分析】本题考查平行直线的判断、同位角和内错角的识别,依次对四个图形中的角进行识别即可得到答案.
【详解】解:①的依据是“同位角相等,两直线平行”;
②的依据是“内错角相等,两直线平行”;
③的依据是“同位角相等,两直线平行”;
④的依据是“内错角相等,两直线平行”;
故选:A.
3.
【分析】根据题意找到同位角,,即可求解.
【详解】解:∵,
∴.
故答案为:.
4. 相等 ∠2
5.解:∵平分,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴.
题型02 内错角相等两直线平行
6.B
【分析】本题考查平行线的判定,掌握平行线的判定条件:同位角相等、内错角相等、同旁内角互补是解题关键.结合三角板的特点,根据平行线的判定条件逐一判断即可.
【详解】解:图(1),根据同位角相等,两直线平行得出,不符合题意;
图(2),,,符合题意;
图(3),,根据同旁内角互补两直线平行得到,不符合题意;
图(4),,,符合题意;
即能得出的是(2)(4),
故选:B.
7.
【分析】本题考查了三线八角,以及平行线的判定,根据“内错角相等,两直线平行”解答即可.
【详解】解:∵,
∴.
故答案为:.
8.(答案不唯一)
9.解:可以判断,理由如下:
∵,平分,
∴.
∵,
∴,
∴.
10.证明:∵,,
∴,
∵平分,
∴,
∴,
∴.
题型03 同旁内角互补两直线平行
11.B
【分析】本题考查了平行线的判定方法:①两同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行.根据平行线的判定方法逐项分析即可.
【详解】解:A.,根据内错角相等,两直线平行可得,故不符合题意;
B.,根据同旁内角互补,两直线平行可得,故符合题意;
C.∠5=∠B,根据两同位角相等,两直线平行可得,故不符合题意;
D.,根据同旁内角互补,两直线平行可得,故不符合题意;
故选B.
12.C
【分析】此题考查了平行线的判定,根据平行线的判定定理求解即可.
【详解】A.∵和是同位角,
∴无法推出,不符合题意;
B.∵和是内错角,
∴无法推出,不符合题意;
C.如图所示,
∵,
∵
∴
∴,符合题意;
D.如图所示,
∵,
∴
∵和是同位角,
∴无法推出,故不符合题意;
故选:C.
13.(答案不唯一)
【分析】本题主要考查了平行线的判定,熟练掌握平行线的判定方法是解决问题的关键.根据平行线的判定即可得到结论.
【详解】解:添加:,
,,
,
,
故答案为:(答案不唯一).
14.
【分析】本题主要考查了三角板中的角度计算,平行线的判定,根据,利用同旁内角互补,两直线平行直接求出结论.
【详解】解:,
当时,,
即当时,,
故答案为:
15.解:与平行,理由如下:
平分,,
,
,
,
.
题型04 垂直于同一直线的两直线平行
16.C
【分析】根据平行公理的推论进行分析判断即可.
【详解】解:A.如果,,那么,故A正确,不符合题意;
B.如果,a∥c,那么b∥c,故B正确,不符合题意;
CD.如果a⊥b,,那么,而不是,故C错误,符合题意,D正确不符合题意.
故选:C.
17.C
【分析】根据平行公理,平行线的判定方法逐一分析判断即可.
【详解】解:A据平行于同一条直线的两直线互相平行,可得,不符合题意;
B据同一平面内,垂直于同一条直线两直线平行,可得,不符合题意;
C中据垂直于两平行线中一条的直线必与另一条垂直,可得,符合题意;
D中内错角的邻补角相等即内错角相等,可得,不符合题意;
故选C.
18.D
【分析】根据平行公理,平行线的判定定理及性质定理与垂直的性质,逐项进行分析,即可找到答案.
【详解】解:A、由,,不能得到,原命题是假命题,不符合题意;
B、同一平面内,a⊥b,,则a∥c,原命题是假命题,不符合题意;
C、同一平面内,a⊥b,,则,原命题是假命题,不符合题意;
D、若a⊥b,,则,原命题是真命题,符合题意;
故选D.
19. 平行 平行
【分析】根据平行线的性质和规律得到:4条直线的位置关系为一个循环.
【详解】如图,a1⊥a2,a2∥a3,
∴a1⊥a3,
∵a3⊥a4,
∴a1∥a4,
∵a4∥a5,
∴a1∥a5,
…,
依此类推,a1⊥a6,a1⊥a7,a1∥a8,a1∥a9,连续4条直线的位置关系为一个循环.
∴2021=505×4+1,
∴a1∥a2021.
故答案是:平行;平行.
20.解:、、为同一平面内三条直线,
根据平行于同一条直线的两条直线平行即可由①②得到⑤.
(或者是根据垂直于同一直线的两直线平行也能得出正确答案.)
故答案为: ,(或,或a⊥b,等).
题型05 平行线判定方法的结合问题
21.B
【分析】本题主要考查了平行线的判定定理,根据平行线的判定定理分别进行判断即可.
【详解】解:①当,可以根据同旁内角互补两直线平行得到,故①正确;
②当时,不可以推出,故②错误;
③当时,不可以推出,故③错误;
④当时,可以根据同位角相等,两直线平行得到,故④正确.
∴正确的有2个.
故选:B.
22.B
【分析】本题考查了平行线的判定,掌握平行线的判定定理是解题关键.根据内错角相等,同旁内角互补逐一判断平行即可.
【详解】解:A、,由“内错角相等,两直线平行”可判断,不符合题意;
B、,由“内错角相等,两直线平行”可判断,不能判断,符合题意;
C、,由“内错角相等,两直线平行”可判断,不符合题意;
D、,由“同旁内角互补,两直线平行”可判断,不符合题意;
故选:B.
23.A
【分析】本题主要考查了平行线的判定定理,熟知同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,两直线平行是解题的关键.
【详解】解:由,可以根据同旁内角互补,两直线平行得到,故①符合题意;
由,可以根据同位角相等,两直线平行得到,故②符合题意;
由,可以根据内错角相等,两直线平行得到,不可以得到,故③不符合题意;
由,可以根据内错角相等,两直线平行得到,故④符合题意;
由,可以根据内错角相等,两直线平行得到,不可以得到,故⑤不符合题意;
由,可以根据同旁内角互补,两直线平行得到,不可以得到,故⑥不符合题意;
故选:A.
24.D
【分析】本题考查了平行线的判定、对顶角相等.根据同位角相等两直线平行,即可判断①;根据内错角相等两直线平行,即可判断②;根据对顶角相等和同旁内角互补两直线平行,即可判断③;根据对顶角相等和同旁内角互补两直线平行,即可判断④,综合即可得出答案.
【详解】解:∵,
∴,故①正确;
∵,
∴,故②正确;
∵,
又∵,
∴,
∴,故③正确;
∵,,
又∵,
∴,
∴不能推出,故④不正确,
综上可得:能判断的条件是①②③.
故选:D.
25.(2)(4)(5)
【分析】本题主要考查了平行线的判定.根据平行线的判定定理,逐项判断即可求解.
【详解】解:(1),则;
(2),则;
(3),则;
(4),则;
(5),则;
(6),则,
所以能判断出的条件有(2)(4)(5).
故答案为:(2)(4)(5)
题型06 平行线的判定(填空型大题)
26.证明:∵,,
∴(垂直的定义),
∴,,
又∵(已知),
∴(等角的余角相等),
∴(内错角相等,两直线平行).
故答案为:垂直的定义;;;;等角的余角相等;内错角相等,两直线平行.
27.证明:∵∠AQB=180°
∴∠AQP=∠AQB=90°.理由是:(角平分线的定义).
∵,
∴.理由是:(垂直定义).
∴∠AQP+∠CPQ=180°,
∴.理由是:(同旁内角互补,两直线平行).
故答案为:;90;;垂直定义;∠AQP+∠CPQ=180°;同旁内角互补,两直线平行.
28.证明:∵平分(已知),
∴(角平分线的定义)
∵平分(已知),
∴(角平分线的定义)
∴(等量代换)
∵(已知),
∴(等量代换)
∴(同旁内角互补,两直线平行)
29.证明:(已知).
(垂直的定义)
.
.(已知).
(同角的余角相等).
∴(内错角相等,两直线平行).
30.证明:(已知),
∴(垂直的定义),
,(已知),
,
即,
(同旁内角互补,两直线平行).
题型07 平行线的判定综合
31.(1)解:平行,理由如下:
∵平分,平分,
∴,
∵,
∴,
∴;
(2),理由如下:
∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
∴.
32.(1)解:与的位置关系是:,理由如下:
,
,
,
,
又,
,
;
(2)与不平行,添加条件或时,,理由如下:
当时,
,
,
;
当时,
,
,
;
当时,
,
,
,
,
.
33.解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
34.(1)解:∵∠PAD=32°,
∴,
∵,
∴∠PAB=180°-32°-32°=116°;
(2)证明:∵,,,
∴,
∵,,
∴,
∴,
∴.
35.(1)解:∵平分,
∴,
∵,
∴设,则,
∴,
解得:,
∴;
(2)证明:∵,分别平分和,
∴,,
∴,
∵,
∴,
∴.
题型01 同位角相等两直线平行
1.如图,木工师傅用图中的角尺画平行线的依据是( )
A.同位角相等,两直线平行
B.平行于同一条直线的两条直线平行
C.经过直线外一点,有且只有一条直线与这条直线平行两直线平行,同位角相等
D.两直线平行,同位角相等
2.下列各图中,的依据是“同位角相等,两直线平行”的是( )
A.①③ B.①②④ C.③④ D.①②③④
3.结合下图,用符号语言表达定理“同位角相等,两直线平行”的推理形式:∵ ,∴.
4.两条平行直线被第三条直线所截,同位角相等.
简称:两直线平行,同位角 .
如图,因为a∥b,(已知)
所以∠1= .(两直线平行,同位角相等)
5.如图,直线,相交于点,平分,平分,,垂足为,试说明:.
题型02 内错角相等两直线平行
6.下列各图是由含或的直角三角板组合而成,其中利用内错角相等,画出的有( )
A.(1)(3) B.(2)(4) C.(1)(2)(4) D.(2)(3)(4)
7.如图,用符号语言表达定理“内错角相等,两直线平行”的推理形式:∵ ,∴.
8.如图,四边形,点在的延长线上,依据“内错角相等,两直线平行”来判断,可选择的一组内错角是 .(填一种答案即可)
9.如图所示,已知,,平分,可以判断吗?为什么?
10.已知如图所示,,点、、在同一条直线上,,且平分,证明:.
题型03 同旁内角互补两直线平行
11.如图,点,,在一条直线上,要根据“同旁内角互补,两直线平行”判定,需添加的一个条件是( )
A. B.
C.∠5=∠B D.
12.若,则下列图形一定能推出的是( )
A. B. C. D.
13.如图是一款教室的日光灯管,用两根线,吊在天花板上,为了保护眼睛,使空间内光线更匀称,不易反光,需使灯管与天花板平行,已知,请你添加一个条件: ,使灯管与天花板平行.
14.把一副三角板(,,)按如图所示的方式摆放,当为 度时,.
15.如图,在四边形中,,平分,且,.与平行吗?试写出推理过程.
题型04 垂直于同一直线的两直线平行
16.已知在同一平面内有三条不同的直线,,,下列说法错误的是( )
A.如果,,那么 B.如果,a∥c,那么b∥c
C.如果a⊥b,,那么 D.如果a⊥b,,那么b∥c
17.a,b,c为平面内不同的三条直线,若要,条件不符合的是( )
A., B.a⊥b,
C., D.c截a,b所得的内错角的邻补角相等
18.下列命题中的真命题是( )
A.若,,则 B.若a⊥b,,则
C.若a⊥b,,则 D.若a⊥b,,则
19.在同一平面内有2021条直线a1,a2,a3,…,a2021,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,那么a1与a5的位置关系是 ;a1与a2021的位置关系是 .
20.对于同一平面内三条直线、、有以下论断:
①;②;③;④;⑤.
请以其中两个论断为条件,一个论断为结论,组成一个真命题.
题型05 平行线判定方法的结合问题
21.如图,下列能判定的条件的个数是( )
①;②;③;④
A.1个 B.2个 C.3个 D.4个
22.如图,点在的延长线上,下列条件中不能判断的是( )
A. B.
C. D.
23.如图,点在的延长线上,给出下列条件:
①;②;③;④,⑤,⑥
一定能判定的条件有( )
A.个 B.个 C.个 D.个
24.如图,直线a、b都与直线c相交,给出下列条件:①;②;③;④.其中能判断的条件是( )
A.①② B.③④ C.①③④ D.①②③
25.如图,点E在的延长线上,给出下列条件:
(1);(2);(3);(4);(5);(6),能判断出的条件有 .(填序号)
题型06 平行线的判定(填空型大题)
26.请完善下列题目的解答过程,并在括号内填写相应的理论依据.
已知:如图,,且,求证:.
解:∵,,
∴( )
∴,,
又∵(已知)
∴______=______( )
∴( )
27.如图1,在数学活动课上,同学们探究过直线外一点P画的方法,其中王玲是通过折纸的方式完成:
第一步:如图2,过点P进行第一次折叠,使点B的对称点B 落在上,折痕与相交于点Q,打开纸张铺平;
第二步:如图3,过点P进行第二次折叠,使折痕,打开纸张铺平(如图4);
王玲就说,你能用几何推理说说其中的道理吗?
(请完成下面的证明,并填上对应的推理根据)
证明:∵∠AQB=180°
∴∠ ∠AQB= .理由是:(角平分线的定义).
∵,
∴∠ .理由是:( ).
∴ ,
∴.理由是:( ).
28.完成下面的证明:
如图,平分,平分,且,求证.
证明:∵平分(已知),
∴( )
∵平分(已知),
∴_________( )
∴( )
∵(已知),
∴_________( )
∴( )
29.完成下面推理及填空:
已知:如图,在 ABC中,于点是上一点,且,求证:.
证明:(已知).
_______( )
______.
.( ).
______(______).
∴______( ).
30.完成下面的证明:
已知:如图,,,.求证:.
证明:(________)
________(________)
,(已知)
________
即________
(________)
题型07 平行线的判定综合
31.如图,已知平分,平分,且.
(1)与平行吗? 为什么?
(2)请判断与的位置关系,并说明理由.
32.如图,,,.
(1)与有怎样的位置关系?为什么?
(2)与平行吗?若平行,请说明理由;若不平行,那么再加上什么条件就平行了呢?
33.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知,.请你用所学知识来判断c与d是否平行?并说明理由.
34.如图,台球运动中母球击中桌边的点,经桌边反弹后击中相邻的另一桌边的点,再次反弹经过点,其中,.
(1)若∠PAD=32°,求的度数;
(2)已知,求证:.
35.如图,直线与直线,分别相交于点M,O,,分别平分和,与交于点P,Q,已知.
(1)若,求的度数;
(2)对说明理由.
参考答案
题型01 同位角相等两直线平行
1.A
【分析】本题考查了平行线的判定.解题的关键在于对知识的熟练掌握与灵活运用.根据平行线的判定进行解答即可.
【详解】解:由题意知,木工用图中的角尺画平行线的依据是:同位角相等,两直线平行,
故选:A.
2.A
【分析】本题考查平行直线的判断、同位角和内错角的识别,依次对四个图形中的角进行识别即可得到答案.
【详解】解:①的依据是“同位角相等,两直线平行”;
②的依据是“内错角相等,两直线平行”;
③的依据是“同位角相等,两直线平行”;
④的依据是“内错角相等,两直线平行”;
故选:A.
3.
【分析】根据题意找到同位角,,即可求解.
【详解】解:∵,
∴.
故答案为:.
4. 相等 ∠2
5.解:∵平分,
∴,
∵平分,
∴,
∴,
∵,
∴,
∴,
∴.
题型02 内错角相等两直线平行
6.B
【分析】本题考查平行线的判定,掌握平行线的判定条件:同位角相等、内错角相等、同旁内角互补是解题关键.结合三角板的特点,根据平行线的判定条件逐一判断即可.
【详解】解:图(1),根据同位角相等,两直线平行得出,不符合题意;
图(2),,,符合题意;
图(3),,根据同旁内角互补两直线平行得到,不符合题意;
图(4),,,符合题意;
即能得出的是(2)(4),
故选:B.
7.
【分析】本题考查了三线八角,以及平行线的判定,根据“内错角相等,两直线平行”解答即可.
【详解】解:∵,
∴.
故答案为:.
8.(答案不唯一)
9.解:可以判断,理由如下:
∵,平分,
∴.
∵,
∴,
∴.
10.证明:∵,,
∴,
∵平分,
∴,
∴,
∴.
题型03 同旁内角互补两直线平行
11.B
【分析】本题考查了平行线的判定方法:①两同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行.根据平行线的判定方法逐项分析即可.
【详解】解:A.,根据内错角相等,两直线平行可得,故不符合题意;
B.,根据同旁内角互补,两直线平行可得,故符合题意;
C.∠5=∠B,根据两同位角相等,两直线平行可得,故不符合题意;
D.,根据同旁内角互补,两直线平行可得,故不符合题意;
故选B.
12.C
【分析】此题考查了平行线的判定,根据平行线的判定定理求解即可.
【详解】A.∵和是同位角,
∴无法推出,不符合题意;
B.∵和是内错角,
∴无法推出,不符合题意;
C.如图所示,
∵,
∵
∴
∴,符合题意;
D.如图所示,
∵,
∴
∵和是同位角,
∴无法推出,故不符合题意;
故选:C.
13.(答案不唯一)
【分析】本题主要考查了平行线的判定,熟练掌握平行线的判定方法是解决问题的关键.根据平行线的判定即可得到结论.
【详解】解:添加:,
,,
,
,
故答案为:(答案不唯一).
14.
【分析】本题主要考查了三角板中的角度计算,平行线的判定,根据,利用同旁内角互补,两直线平行直接求出结论.
【详解】解:,
当时,,
即当时,,
故答案为:
15.解:与平行,理由如下:
平分,,
,
,
,
.
题型04 垂直于同一直线的两直线平行
16.C
【分析】根据平行公理的推论进行分析判断即可.
【详解】解:A.如果,,那么,故A正确,不符合题意;
B.如果,a∥c,那么b∥c,故B正确,不符合题意;
CD.如果a⊥b,,那么,而不是,故C错误,符合题意,D正确不符合题意.
故选:C.
17.C
【分析】根据平行公理,平行线的判定方法逐一分析判断即可.
【详解】解:A据平行于同一条直线的两直线互相平行,可得,不符合题意;
B据同一平面内,垂直于同一条直线两直线平行,可得,不符合题意;
C中据垂直于两平行线中一条的直线必与另一条垂直,可得,符合题意;
D中内错角的邻补角相等即内错角相等,可得,不符合题意;
故选C.
18.D
【分析】根据平行公理,平行线的判定定理及性质定理与垂直的性质,逐项进行分析,即可找到答案.
【详解】解:A、由,,不能得到,原命题是假命题,不符合题意;
B、同一平面内,a⊥b,,则a∥c,原命题是假命题,不符合题意;
C、同一平面内,a⊥b,,则,原命题是假命题,不符合题意;
D、若a⊥b,,则,原命题是真命题,符合题意;
故选D.
19. 平行 平行
【分析】根据平行线的性质和规律得到:4条直线的位置关系为一个循环.
【详解】如图,a1⊥a2,a2∥a3,
∴a1⊥a3,
∵a3⊥a4,
∴a1∥a4,
∵a4∥a5,
∴a1∥a5,
…,
依此类推,a1⊥a6,a1⊥a7,a1∥a8,a1∥a9,连续4条直线的位置关系为一个循环.
∴2021=505×4+1,
∴a1∥a2021.
故答案是:平行;平行.
20.解:、、为同一平面内三条直线,
根据平行于同一条直线的两条直线平行即可由①②得到⑤.
(或者是根据垂直于同一直线的两直线平行也能得出正确答案.)
故答案为: ,(或,或a⊥b,等).
题型05 平行线判定方法的结合问题
21.B
【分析】本题主要考查了平行线的判定定理,根据平行线的判定定理分别进行判断即可.
【详解】解:①当,可以根据同旁内角互补两直线平行得到,故①正确;
②当时,不可以推出,故②错误;
③当时,不可以推出,故③错误;
④当时,可以根据同位角相等,两直线平行得到,故④正确.
∴正确的有2个.
故选:B.
22.B
【分析】本题考查了平行线的判定,掌握平行线的判定定理是解题关键.根据内错角相等,同旁内角互补逐一判断平行即可.
【详解】解:A、,由“内错角相等,两直线平行”可判断,不符合题意;
B、,由“内错角相等,两直线平行”可判断,不能判断,符合题意;
C、,由“内错角相等,两直线平行”可判断,不符合题意;
D、,由“同旁内角互补,两直线平行”可判断,不符合题意;
故选:B.
23.A
【分析】本题主要考查了平行线的判定定理,熟知同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,两直线平行是解题的关键.
【详解】解:由,可以根据同旁内角互补,两直线平行得到,故①符合题意;
由,可以根据同位角相等,两直线平行得到,故②符合题意;
由,可以根据内错角相等,两直线平行得到,不可以得到,故③不符合题意;
由,可以根据内错角相等,两直线平行得到,故④符合题意;
由,可以根据内错角相等,两直线平行得到,不可以得到,故⑤不符合题意;
由,可以根据同旁内角互补,两直线平行得到,不可以得到,故⑥不符合题意;
故选:A.
24.D
【分析】本题考查了平行线的判定、对顶角相等.根据同位角相等两直线平行,即可判断①;根据内错角相等两直线平行,即可判断②;根据对顶角相等和同旁内角互补两直线平行,即可判断③;根据对顶角相等和同旁内角互补两直线平行,即可判断④,综合即可得出答案.
【详解】解:∵,
∴,故①正确;
∵,
∴,故②正确;
∵,
又∵,
∴,
∴,故③正确;
∵,,
又∵,
∴,
∴不能推出,故④不正确,
综上可得:能判断的条件是①②③.
故选:D.
25.(2)(4)(5)
【分析】本题主要考查了平行线的判定.根据平行线的判定定理,逐项判断即可求解.
【详解】解:(1),则;
(2),则;
(3),则;
(4),则;
(5),则;
(6),则,
所以能判断出的条件有(2)(4)(5).
故答案为:(2)(4)(5)
题型06 平行线的判定(填空型大题)
26.证明:∵,,
∴(垂直的定义),
∴,,
又∵(已知),
∴(等角的余角相等),
∴(内错角相等,两直线平行).
故答案为:垂直的定义;;;;等角的余角相等;内错角相等,两直线平行.
27.证明:∵∠AQB=180°
∴∠AQP=∠AQB=90°.理由是:(角平分线的定义).
∵,
∴.理由是:(垂直定义).
∴∠AQP+∠CPQ=180°,
∴.理由是:(同旁内角互补,两直线平行).
故答案为:;90;;垂直定义;∠AQP+∠CPQ=180°;同旁内角互补,两直线平行.
28.证明:∵平分(已知),
∴(角平分线的定义)
∵平分(已知),
∴(角平分线的定义)
∴(等量代换)
∵(已知),
∴(等量代换)
∴(同旁内角互补,两直线平行)
29.证明:(已知).
(垂直的定义)
.
.(已知).
(同角的余角相等).
∴(内错角相等,两直线平行).
30.证明:(已知),
∴(垂直的定义),
,(已知),
,
即,
(同旁内角互补,两直线平行).
题型07 平行线的判定综合
31.(1)解:平行,理由如下:
∵平分,平分,
∴,
∵,
∴,
∴;
(2),理由如下:
∵,
∴,
∵,
∴,
∵平分,
∴,
∴,
∴.
32.(1)解:与的位置关系是:,理由如下:
,
,
,
,
又,
,
;
(2)与不平行,添加条件或时,,理由如下:
当时,
,
,
;
当时,
,
,
;
当时,
,
,
,
,
.
33.解:,理由如下:
∵,,
∴,
∵,
∴,
∴.
34.(1)解:∵∠PAD=32°,
∴,
∵,
∴∠PAB=180°-32°-32°=116°;
(2)证明:∵,,,
∴,
∵,,
∴,
∴,
∴.
35.(1)解:∵平分,
∴,
∵,
∴设,则,
∴,
解得:,
∴;
(2)证明:∵,分别平分和,
∴,,
∴,
∵,
∴,
∴.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
