5.1 分式的意义 课件(共15张PPT) 浙教版(2024)数学七年级下册
文档属性
| 名称 | 5.1 分式的意义 课件(共15张PPT) 浙教版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 318.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-22 11:47:43 | ||
图片预览






文档简介
(共15张PPT)
5.1 分式的意义
学习目标
1.了解分式的概念;
2..了解分式有意义,分式值为零的条件;
3.会用分式表示简单实际问题中的数量关系.
2、观察下列代数式
你能用两个整式的比值的形式表示它们吗?
7÷p,b÷a,(v-v0)÷t,(2x-3)÷(x+2),
1、下列代数式中,哪些是整式?哪些不是整式?
整式:
分式的概念:
两个整式相除,如果除式中含有字母,像这样的代数式叫做分式.
整式A除以B整式,可以表示成 的形式.
如果分母中含有字母,那么称 为分式.
试一试:你能举一些分式的例子吗?
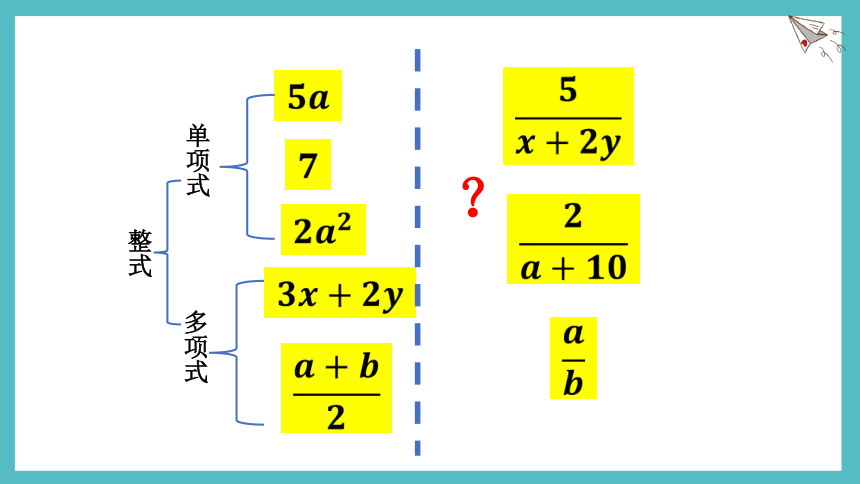
辩一辩:下列哪些是分式?
?
单项式
多项式
整式
(1)把分式 具体化,用具体的数值代替字母a,求分式的值.
(2)字母a的取值有什么要求吗?
探究:
归纳:分式 的意义:
b=0 分式无意义
b≠0 分式有意义
a=0且b≠0 分式的值是零。
例1 对于分式
(1)当x取什么数时,分式有意义?
(2)当x取什么数时,分式的值为零?
(3)当x=1时,分式的值是多少?
(1)当分母等于零时,分式无意义;
(2)当分母不等于零时,分式有意义;
(3)当分子等于零且分母不等于0时,分式的值为零.
归纳:
例2 甲、乙两人从同一条公路出发,同向而行.已知甲每小时行a千米,乙每小时行b千米,a>b.如果乙提前1小时出发,那么甲追上乙需要多少时间?当a=6,b=5时,甲追上乙需要的时间.
解:由题意,小明先行1小时的路程是1×b=b(千米),小丁比小明每小时多行(a-b)千米,所以小丁追上小明所需的时间是
b
小明
小丁
b÷ (a-b)= (时)
B
2.一辆汽车行驶a千米用b小时,它的平均车速为________千米/时;一列火车行驶a千米比这辆汽车少用1小时,它的平均速度为___________千米/时.
A.x≠2 B.x≠-2
C.x≠2且x≠-2 D.x≠2或x≠-2
【解析】 分式有意义的条件是分母不为零,即(x+2)(x-2)≠0.故选择C.
1.分式的概念
定义:表示两个整式________,且除式中含有________.像这样的代数式叫做分式.相除 字母
2.分式有意义的条件
条件:(1)分式中字母的取值不能使分母为______;零
(2)当分母的值为零时,分式就________意义.没有
分式为零的条件:分子为零,且分母不为零,分式的值为零.
3.注意:
(1)分式是否有意义,看分母
①分母为零,分式无意义.
②分母不为零,分式有意义.
(2)要使分式的值为零,必须同时满足分子为零且分母不为零.
5.1 分式的意义
学习目标
1.了解分式的概念;
2..了解分式有意义,分式值为零的条件;
3.会用分式表示简单实际问题中的数量关系.
2、观察下列代数式
你能用两个整式的比值的形式表示它们吗?
7÷p,b÷a,(v-v0)÷t,(2x-3)÷(x+2),
1、下列代数式中,哪些是整式?哪些不是整式?
整式:
分式的概念:
两个整式相除,如果除式中含有字母,像这样的代数式叫做分式.
整式A除以B整式,可以表示成 的形式.
如果分母中含有字母,那么称 为分式.
试一试:你能举一些分式的例子吗?
辩一辩:下列哪些是分式?
?
单项式
多项式
整式
(1)把分式 具体化,用具体的数值代替字母a,求分式的值.
(2)字母a的取值有什么要求吗?
探究:
归纳:分式 的意义:
b=0 分式无意义
b≠0 分式有意义
a=0且b≠0 分式的值是零。
例1 对于分式
(1)当x取什么数时,分式有意义?
(2)当x取什么数时,分式的值为零?
(3)当x=1时,分式的值是多少?
(1)当分母等于零时,分式无意义;
(2)当分母不等于零时,分式有意义;
(3)当分子等于零且分母不等于0时,分式的值为零.
归纳:
例2 甲、乙两人从同一条公路出发,同向而行.已知甲每小时行a千米,乙每小时行b千米,a>b.如果乙提前1小时出发,那么甲追上乙需要多少时间?当a=6,b=5时,甲追上乙需要的时间.
解:由题意,小明先行1小时的路程是1×b=b(千米),小丁比小明每小时多行(a-b)千米,所以小丁追上小明所需的时间是
b
小明
小丁
b÷ (a-b)= (时)
B
2.一辆汽车行驶a千米用b小时,它的平均车速为________千米/时;一列火车行驶a千米比这辆汽车少用1小时,它的平均速度为___________千米/时.
A.x≠2 B.x≠-2
C.x≠2且x≠-2 D.x≠2或x≠-2
【解析】 分式有意义的条件是分母不为零,即(x+2)(x-2)≠0.故选择C.
1.分式的概念
定义:表示两个整式________,且除式中含有________.像这样的代数式叫做分式.相除 字母
2.分式有意义的条件
条件:(1)分式中字母的取值不能使分母为______;零
(2)当分母的值为零时,分式就________意义.没有
分式为零的条件:分子为零,且分母不为零,分式的值为零.
3.注意:
(1)分式是否有意义,看分母
①分母为零,分式无意义.
②分母不为零,分式有意义.
(2)要使分式的值为零,必须同时满足分子为零且分母不为零.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
