七年级数学下册浙教版 3.4 《乘法公式》小节复习题(含答案)
文档属性
| 名称 | 七年级数学下册浙教版 3.4 《乘法公式》小节复习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 901.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-23 10:03:35 | ||
图片预览



文档简介
3.4 《乘法公式》小节复习题
题型01 运用平方差公式进行运算
1.的计算结果是( )
A. B. C.2 D.4
2.在下列多项式乘法中,可以用平方差公式计算的是( )
A. B.
C. D.
3.( ).
4.计算的结果为 .
5.用平方差公式计算:
(1); (2); (3); (4).
题型02 平方差公式与几何图形
6.如图①,从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图②.通过计算阴影部分的面积可以得到( )
A. B.
C. D.
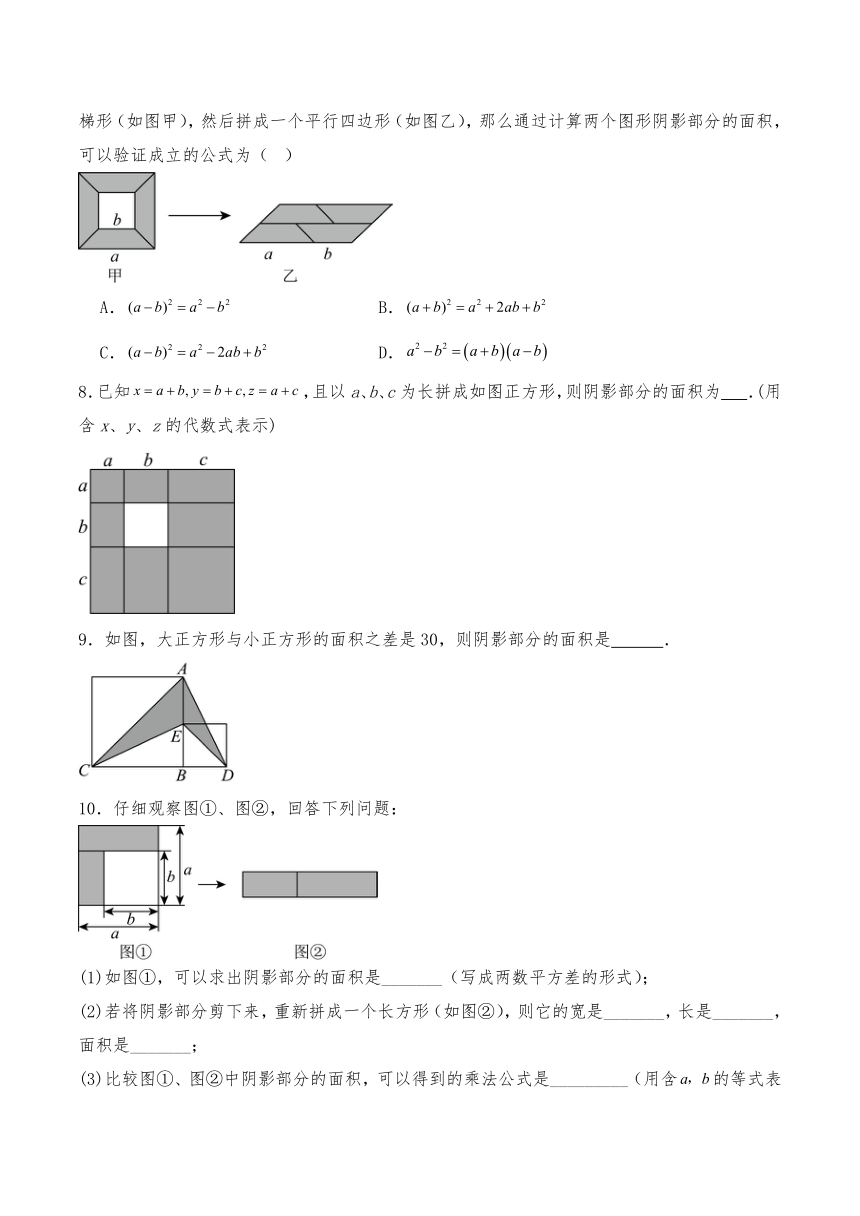
7.从边长为的大正方形纸板挖去一个边长为的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A. B.
C. D.
8.已知,且以a、b、c为长拼成如图正方形,则阴影部分的面积为 .(用含x、y、z的代数式表示)
9.如图,大正方形与小正方形的面积之差是30,则阴影部分的面积是 .
10.仔细观察图①、图②,回答下列问题:
(1)如图①,可以求出阴影部分的面积是_______(写成两数平方差的形式);
(2)若将阴影部分剪下来,重新拼成一个长方形(如图②),则它的宽是_______,长是_______,面积是_______;
(3)比较图①、图②中阴影部分的面积,可以得到的乘法公式是_________(用含的等式表示).
题型03 运用完全平方公式进行运算
11.利用完全平方公式计算,下列变形最恰当的是( )
A. B. C. D.
12.若,则的最小值是( )
A.2014 B.2016 C.2018 D.2020
13.化简的值是 .
14.根据完全平方公式填空:
(1) ;
(2)( ).
15.计算:
(1); (2); (3).
题型04 完全平方公式在几何图形中的应用
16.两个边长为的大正方形与两个边长为的小正方形按如图所示放置,如果,阴影部分的面积是60,那么( )
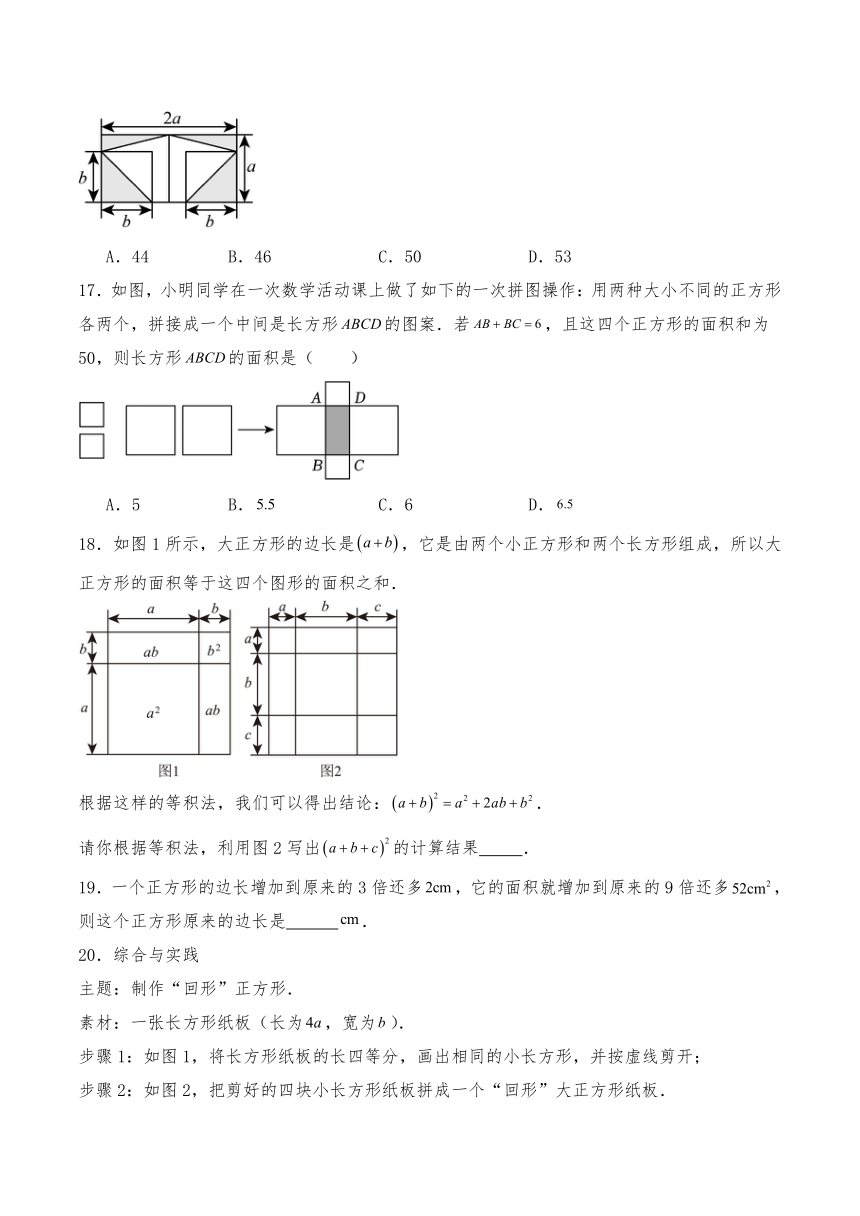
A.44 B.46 C.50 D.53
17.如图,小明同学在一次数学活动课上做了如下的一次拼图操作:用两种大小不同的正方形各两个,拼接成一个中间是长方形的图案.若,且这四个正方形的面积和为50,则长方形的面积是( )
A.5 B. C.6 D.
18.如图1所示,大正方形的边长是,它是由两个小正方形和两个长方形组成,所以大正方形的面积等于这四个图形的面积之和.
根据这样的等积法,我们可以得出结论:.
请你根据等积法,利用图2写出的计算结果 .
19.一个正方形的边长增加到原来的3倍还多,它的面积就增加到原来的9倍还多,则这个正方形原来的边长是 .
20.综合与实践
主题:制作“回形”正方形.
素材:一张长方形纸板(长为,宽为).
步骤1:如图1,将长方形纸板的长四等分,画出相同的小长方形,并按虚线剪开;
步骤2:如图2,把剪好的四块小长方形纸板拼成一个“回形”大正方形纸板.
(1)图2中小正方形(阴影部分)的边长为__________.(用含,的式子表示)
(2)根据图2,请直接写出,,之间的等量关系.
(3)若,,求的值.
拓展与应用
(4)若,求的值.
题型05 乘法公式的知二求三问题
21.已知,求下列代数式的值:
(1); (2).
22.已知,求:
(1)的值; (2)的值.
23.已知,,求的值.
24.已知,.
(1)求的值;
(2)求的值.
25.(1)已知,,求;
(2)已知,,求的值.
题型06 乘法公式中的整体带入方法
26.已知,则的值是( )
A. B. C. D.
27.已知,那么的值为( )
A.4051 B.2025 C.4046 D.4053
28.已知,则的值 .
29.若,则 .
30.阅读:若满足,求的值.
解:设,,
则_____,_____,
所以_____.
请仿照上例解决下面的问题:
(1)补全题目中横线处;
(2)若满足,求的值.
题型07 运用乘法公式解决规律性问题
31.根据等式:,,,的规律,则可以得出的结果为( )
A. B. C. D.
32.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”,揭示了(为非负整数)展开式各项系数的有关规律:
……………………
请你猜想的展开式中所有系数的和是( )
A.2022 B.512 C.128 D.64
33.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(为非负整数)展开式的项数及各项系数的有关规律,
利用上述规律计算: .
34.观察以下等式:
第1个:
第2个:
第3个:
按照以上规律,解决下列问题:
(1)写出第5个等式: .
(2)写出你猜想的第n个等式(用含n的式子表示),并证明.
35.观察下列各式
···
①根据以上规律,则 ,
②由此归纳出一般性规律: ;
③根据②直接写出: .
题型08 乘法公式的新定义问题
36.定义,,给出下列结论错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
37.对于任意有理数A,B,现用“☆”定义一种运算:.根据这个定义,代数式可以化简为( )
A. B. C. D.
38.定义新运算“”,对于任意实数都有.例如:.若,则 .
39.已知对任意实数x,y,定义运算:,则的值为
40.在学习整式乘法一章时,小明定义:若一个整数能表示成(是整数)的形式,则称这个数为“妙数”.例如:10是“妙数”,因为;再如:(是整数),所以也是“妙数”.
(1)判断20是否为“妙数”___________(填“是”或者“否”);
(2)已知(是整数)是常数,要使为“妙数”,试求出符合条件的一个值,并说明理由.
题型01 运用平方差公式进行运算
1.D
【分析】本题考查平方差公式,利用平方差公式进行简算即可.
【详解】解:
;
故选D.
2.B
【分析】本题考查了平方差公式,熟练掌握平方差公式的特点是解题的关键.平方差公式的形式是,平方差公式的特点是两个数的和乘以两个数的差,逐一判断四个选项,即可求解.
【详解】解:A,,不可以用平方差公式计算,不符合题意;
B,,可以用平方差公式计算,符合题意;
C,,不可以用平方差公式计算,不符合题意;
D,,不可以用平方差公式计算,不符合题意.
故选:B.
3.
【分析】本题考查了平方差公式,运用平方差公式变形,即可作答.
【详解】解:.
故答案为:.
4.
【分析】本题考查平方差公式,掌握平方差公式的结构特征是正确解答的关键.
根据平方差公式进行计算即可
【详解】解:,
故答案为:.
5.(1)解:原式.
(2)解:原式.
(3)解:原式.
(4)解:原式.
题型02 平方差公式与几何图形
6.C
【分析】本题主要考查了平方差公式的几何背景,解题的关键是求出第一个图的阴影部分面积,进而根据长方形的面积计算公式求出拼成的长方形的面积,根据面积不变得出结论,这个图形变换可以用来证明平方差公式:已知在左图中,大正方形减小正方形剩下的部分面积为;因为拼成的长方形的长为,宽为,根据“长方形的面积长宽”代入为:,因为面积相等,进而得出结论.
【详解】解:由图可知,大正方形减小正方形剩下的部分面积为;
拼成的长方形的面积:,
所以得出:,
故选:C.
7.D
【分析】本题主要考查了平方差公式,运用不同方法表示阴影部分面积是解题的关键.分别表示出两个图形阴影部分的面积,即可得到答案.
【详解】图甲中阴影部分的面积为:,图乙中阴影部分的面积为:,
∵甲乙两图中阴影部分的面积相等,
∴可以验证成立的公式为.
故选:D.
8.
【分析】本题考查平方差公式与几何图形的面积,利用分割法表示出阴影部分的面积,再根据,结合平方差公式,将面积转化为含x、y、z的代数式即可.
【详解】解:由图可知,阴影部分的面积为:
∵,
∴阴影部分的面积为.
故答案为:.
9.15
【分析】此题考查了平方差公式几何背景问题的解决能力,关键是能准确理解题意,结合图形运用以上知识进行求解.设大正方形和小正方形的边长各为a,b,由题意可得,再运用三角形面积公式进行求解.
【详解】解:设大正方形和小正方形的边长各为,,
由题意可得,
阴影部分的面积为:
=
=
故答案为:15.
10.(1)
(2),,
(3)
【分析】本题考查了平方差公式的几何形式:(1)阴影部分的面积为大正方形减去小正方形的面积,用面积公式求即可;(2)观察图形,阴影部分的宽是小长方形的宽,阴影部分的长是两个小长方形的长之和,再根据长方形的面积公式即可求;(3)利用面积相等即可得到等式.
【详解】(1)阴影部分的面积大正方形的面积小正方形的面积
面积
(2)观察图形,阴影部分的宽是小长方形的宽:
阴影部分的长是两个小长方形的长之和:
所以阴影部分的面积为长方形的面积:
(3)两个阴影部分的面积相同,即.
题型03 运用完全平方公式进行运算
11.A
【分析】本题考查了完全平方公式,选择最简单的计算方式是解题的关键.
选择最简单的计算方式即可.
【详解】解:利用完全平方公式计算,变形最恰当的是,
故选:A.
12.A
【分析】本题考查了完全平方公式的应用等知识,利用完全平方公式将转化为,再根据即可得到的最小值是2014.
【详解】解:
,
∵,
∴M的最小值是2014.
故选:A.
13.
【分析】本题考查了完全平方公式,整式的加减,先根据完全平方公式化简,再去括号合并同类项.
【详解】解:
.
故答案为:.
14. 16 4
【分析】本题考查完全平方公式,掌握完全平方公式是解题的关键.
(1)根据完全平方公式进行解答即可;
(2)根据完全平方公式进行解答即可.
【详解】解:(1);
(2).
故答案为:16;4;
15.(1)解:
;
(2)解:
;
(3)解:
.
题型04 完全平方公式在几何图形中的应用
16.A
【分析】本题考查了完全平方公式的几何背景的应用,根据题意列出阴影部分面积的表达式是解决本题的关键.
由图可得阴影部分面积为个直角三角形面积的和,用含、的式子表示出阴影部分的面积即可求解.
【详解】解:如图:
∵,,
∴,
∴,
,
∴,
解得:.
故选:A .
17.B
【分析】本题主要考查了完全平方式的知识,解决问题的关键是读懂题意,找到所求的量的等量关系.
由题意可得,则,再由可得,则,那么,从而求得答案.
【详解】解:由题意可得,
∴,
∵,
∴,
∴,
∴,
∴,
即长方形的面积是,
故选:B.
18.
【分析】用代数式分别表示图形中各个部分的面积,再根据各个部分面积之间的关系进行解答即可.
本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的关键.
【详解】解:整体上是边长为的正方形,
因此面积为,
拼成大正方形的9个部分的面积和为,
∴,
故答案为:.
19.4
【分析】本题考查了完全平方公式的应用,设这个正方形原来的边长为,则原来的面积就是,边长增加后的面积就是.根据“边长增加后的面积原来面积的9倍”即可列方程解答.
【详解】解:设正方形原来边长为,根据题意得:
,
,
,
解得,
即这个正方形原来的边长为.
故答案为:4.
20.解:(1)由图2可得小正方形(阴影部分)的边长为,
故答案为:;
(2)可得阴影部分面积为:,而阴影部分面积又可表示为,
∴,
∴;
(3)∵,,
∴;
(4)∵,
∴,
∴.
题型05 乘法公式的知二求三问题
21.(1)解:∵,
∴.
(2)解:∵,
∴.
22.(1),
;
(2),
.
23.解:因为,
所以,即.
因为,
所以,
所以.
24.(1)解:因为,,
所以,
所以,
所以;
(2)解:因为由(1)知,
又因为,,
所以
.
25.解:(1)∵,,
∴;
(2)∵,,
∴.
题型06 乘法公式中的整体带入方法
26.B
【分析】本题考查完全平方公式的应用,熟练掌握完全平方公式是解题的关键,根据题意巧妙构造,再利用完全平方公式展开,合并同类项后即可得到答案.
【详解】解:已知,
则,
那么,
整理得:,
则,
故选:B.
27.A
【分析】本题考查了完全平方公式,根据完全平方公式得到,再将代入即可求解,掌握相关知识是解题的关键.
【详解】解:
,
∵,
∴原式,
故选:A.
28.36
【分析】本题考查完全平方公式的几何背景,用不同的代数式表示阴影部分的面积是解决问题的关键.设a=x-2021,b=x-2023,进而得出则,再进行计算即可.
【详解】解:设,则,
所以,
即,
所以,
即.
故答案为:36
29.0或
【分析】本题主要考查了分式的求值,完全平方公式的变形求解,利用分类讨论的思想求解是解题的关键.当时和时,分别代入化简计算,即可作答.
【详解】解:,
或.
当时,;
当时,即,
,
,
,
,
故答案为:或.
30.(1)解:设,,
则,,
所以.
故答案为:30,20,340;
(2)解:设,,
则,,
,
,
,即
.
题型07 运用乘法公式解决规律性问题
31.D
【分析】本题考查了多项式乘多项式,数字类规律问题.先将变形为,根据求出的结果得出规律,即可解答.
【详解】解:
,
.
故选:D.
32.B
【分析】本题通过阅读理解寻找规律,观察已知给出的各式中的所有系数的和可得:(a+b)n(n为非负整数)展开式的各项系数和是2n,问题即得解决.
【详解】解:(a+b)0的展开式的各项系数和为:1=20;
(a+b)1的展开式的各项系数和为:1+1=2=21;
(a+b)2的展开式的各项系数和为:1+2+1=4=22;
(a+b)3的展开式的各项系数和为:1+3+3+1=8=23;
(a+b)4的展开式的各项系数和为:1+4+6+4+1=16=24;
……
∴(a+b)n(n为非负整数)的展开式的各项系数和为:2n.
∴(a+b)9的展开式中所有系数的和是:29=512.
故选:B.
33.
【分析】根据前面的变化规律,计算后解答即可.
【详解】∵
∴.
故答案为:.
34.(1)解:第5个等式为:,
故答案为:;
(2)解:第n个等式为:,
证明:左边,
右边,
左边右边,
等式成立.
35.解:①;
②;
③
.
题型08 乘法公式的新定义问题
36.A
【分析】本题考查了完全平方公式,解题的关键是读懂题意,掌握运算法则.根据完全平方公式,得,,再逐项判断即可.
【详解】解:由完全平方公式,得,,
若,则,,则;
若,则,,
∴和不一定相等,故A错误,B正确;
若,则,
又∵,,
∴,
∴;故C正确,不符合题意;
若,则或,则,故D正确,不符合题意.
故选A.
37.C
【分析】本题考查了整式的混合运算,根据题目中给出的定义利用完全平方公式化简计算即可.
【详解】解:,
,
故选:C.
38.5
【分析】本题考查了平方差公式和代数式求值,解题的关键是根据新定义运算法则得到关于x的等式.根据新运算的定义列出等式,然后再形求解即可.
【详解】解:由题意得:,
整理得:,
.
故答案为:5.
39.
【分析】本题主要考查平方差公式,解题的关键是理解题意;由题意可先求出的值,然后问题可求解.
【详解】解:∵,
∴,
∴;
故答案为.
40.(1)解:,
∴20是“妙数”;
故答案为:是;
(2)解:,理由如下:
.
为“妙数”,
,
题型01 运用平方差公式进行运算
1.的计算结果是( )
A. B. C.2 D.4
2.在下列多项式乘法中,可以用平方差公式计算的是( )
A. B.
C. D.
3.( ).
4.计算的结果为 .
5.用平方差公式计算:
(1); (2); (3); (4).
题型02 平方差公式与几何图形
6.如图①,从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图②.通过计算阴影部分的面积可以得到( )
A. B.
C. D.
7.从边长为的大正方形纸板挖去一个边长为的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙),那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A. B.
C. D.
8.已知,且以a、b、c为长拼成如图正方形,则阴影部分的面积为 .(用含x、y、z的代数式表示)
9.如图,大正方形与小正方形的面积之差是30,则阴影部分的面积是 .
10.仔细观察图①、图②,回答下列问题:
(1)如图①,可以求出阴影部分的面积是_______(写成两数平方差的形式);
(2)若将阴影部分剪下来,重新拼成一个长方形(如图②),则它的宽是_______,长是_______,面积是_______;
(3)比较图①、图②中阴影部分的面积,可以得到的乘法公式是_________(用含的等式表示).
题型03 运用完全平方公式进行运算
11.利用完全平方公式计算,下列变形最恰当的是( )
A. B. C. D.
12.若,则的最小值是( )
A.2014 B.2016 C.2018 D.2020
13.化简的值是 .
14.根据完全平方公式填空:
(1) ;
(2)( ).
15.计算:
(1); (2); (3).
题型04 完全平方公式在几何图形中的应用
16.两个边长为的大正方形与两个边长为的小正方形按如图所示放置,如果,阴影部分的面积是60,那么( )
A.44 B.46 C.50 D.53
17.如图,小明同学在一次数学活动课上做了如下的一次拼图操作:用两种大小不同的正方形各两个,拼接成一个中间是长方形的图案.若,且这四个正方形的面积和为50,则长方形的面积是( )
A.5 B. C.6 D.
18.如图1所示,大正方形的边长是,它是由两个小正方形和两个长方形组成,所以大正方形的面积等于这四个图形的面积之和.
根据这样的等积法,我们可以得出结论:.
请你根据等积法,利用图2写出的计算结果 .
19.一个正方形的边长增加到原来的3倍还多,它的面积就增加到原来的9倍还多,则这个正方形原来的边长是 .
20.综合与实践
主题:制作“回形”正方形.
素材:一张长方形纸板(长为,宽为).
步骤1:如图1,将长方形纸板的长四等分,画出相同的小长方形,并按虚线剪开;
步骤2:如图2,把剪好的四块小长方形纸板拼成一个“回形”大正方形纸板.
(1)图2中小正方形(阴影部分)的边长为__________.(用含,的式子表示)
(2)根据图2,请直接写出,,之间的等量关系.
(3)若,,求的值.
拓展与应用
(4)若,求的值.
题型05 乘法公式的知二求三问题
21.已知,求下列代数式的值:
(1); (2).
22.已知,求:
(1)的值; (2)的值.
23.已知,,求的值.
24.已知,.
(1)求的值;
(2)求的值.
25.(1)已知,,求;
(2)已知,,求的值.
题型06 乘法公式中的整体带入方法
26.已知,则的值是( )
A. B. C. D.
27.已知,那么的值为( )
A.4051 B.2025 C.4046 D.4053
28.已知,则的值 .
29.若,则 .
30.阅读:若满足,求的值.
解:设,,
则_____,_____,
所以_____.
请仿照上例解决下面的问题:
(1)补全题目中横线处;
(2)若满足,求的值.
题型07 运用乘法公式解决规律性问题
31.根据等式:,,,的规律,则可以得出的结果为( )
A. B. C. D.
32.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”,揭示了(为非负整数)展开式各项系数的有关规律:
……………………
请你猜想的展开式中所有系数的和是( )
A.2022 B.512 C.128 D.64
33.我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”(如图),此图揭示了(为非负整数)展开式的项数及各项系数的有关规律,
利用上述规律计算: .
34.观察以下等式:
第1个:
第2个:
第3个:
按照以上规律,解决下列问题:
(1)写出第5个等式: .
(2)写出你猜想的第n个等式(用含n的式子表示),并证明.
35.观察下列各式
···
①根据以上规律,则 ,
②由此归纳出一般性规律: ;
③根据②直接写出: .
题型08 乘法公式的新定义问题
36.定义,,给出下列结论错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
37.对于任意有理数A,B,现用“☆”定义一种运算:.根据这个定义,代数式可以化简为( )
A. B. C. D.
38.定义新运算“”,对于任意实数都有.例如:.若,则 .
39.已知对任意实数x,y,定义运算:,则的值为
40.在学习整式乘法一章时,小明定义:若一个整数能表示成(是整数)的形式,则称这个数为“妙数”.例如:10是“妙数”,因为;再如:(是整数),所以也是“妙数”.
(1)判断20是否为“妙数”___________(填“是”或者“否”);
(2)已知(是整数)是常数,要使为“妙数”,试求出符合条件的一个值,并说明理由.
题型01 运用平方差公式进行运算
1.D
【分析】本题考查平方差公式,利用平方差公式进行简算即可.
【详解】解:
;
故选D.
2.B
【分析】本题考查了平方差公式,熟练掌握平方差公式的特点是解题的关键.平方差公式的形式是,平方差公式的特点是两个数的和乘以两个数的差,逐一判断四个选项,即可求解.
【详解】解:A,,不可以用平方差公式计算,不符合题意;
B,,可以用平方差公式计算,符合题意;
C,,不可以用平方差公式计算,不符合题意;
D,,不可以用平方差公式计算,不符合题意.
故选:B.
3.
【分析】本题考查了平方差公式,运用平方差公式变形,即可作答.
【详解】解:.
故答案为:.
4.
【分析】本题考查平方差公式,掌握平方差公式的结构特征是正确解答的关键.
根据平方差公式进行计算即可
【详解】解:,
故答案为:.
5.(1)解:原式.
(2)解:原式.
(3)解:原式.
(4)解:原式.
题型02 平方差公式与几何图形
6.C
【分析】本题主要考查了平方差公式的几何背景,解题的关键是求出第一个图的阴影部分面积,进而根据长方形的面积计算公式求出拼成的长方形的面积,根据面积不变得出结论,这个图形变换可以用来证明平方差公式:已知在左图中,大正方形减小正方形剩下的部分面积为;因为拼成的长方形的长为,宽为,根据“长方形的面积长宽”代入为:,因为面积相等,进而得出结论.
【详解】解:由图可知,大正方形减小正方形剩下的部分面积为;
拼成的长方形的面积:,
所以得出:,
故选:C.
7.D
【分析】本题主要考查了平方差公式,运用不同方法表示阴影部分面积是解题的关键.分别表示出两个图形阴影部分的面积,即可得到答案.
【详解】图甲中阴影部分的面积为:,图乙中阴影部分的面积为:,
∵甲乙两图中阴影部分的面积相等,
∴可以验证成立的公式为.
故选:D.
8.
【分析】本题考查平方差公式与几何图形的面积,利用分割法表示出阴影部分的面积,再根据,结合平方差公式,将面积转化为含x、y、z的代数式即可.
【详解】解:由图可知,阴影部分的面积为:
∵,
∴阴影部分的面积为.
故答案为:.
9.15
【分析】此题考查了平方差公式几何背景问题的解决能力,关键是能准确理解题意,结合图形运用以上知识进行求解.设大正方形和小正方形的边长各为a,b,由题意可得,再运用三角形面积公式进行求解.
【详解】解:设大正方形和小正方形的边长各为,,
由题意可得,
阴影部分的面积为:
=
=
故答案为:15.
10.(1)
(2),,
(3)
【分析】本题考查了平方差公式的几何形式:(1)阴影部分的面积为大正方形减去小正方形的面积,用面积公式求即可;(2)观察图形,阴影部分的宽是小长方形的宽,阴影部分的长是两个小长方形的长之和,再根据长方形的面积公式即可求;(3)利用面积相等即可得到等式.
【详解】(1)阴影部分的面积大正方形的面积小正方形的面积
面积
(2)观察图形,阴影部分的宽是小长方形的宽:
阴影部分的长是两个小长方形的长之和:
所以阴影部分的面积为长方形的面积:
(3)两个阴影部分的面积相同,即.
题型03 运用完全平方公式进行运算
11.A
【分析】本题考查了完全平方公式,选择最简单的计算方式是解题的关键.
选择最简单的计算方式即可.
【详解】解:利用完全平方公式计算,变形最恰当的是,
故选:A.
12.A
【分析】本题考查了完全平方公式的应用等知识,利用完全平方公式将转化为,再根据即可得到的最小值是2014.
【详解】解:
,
∵,
∴M的最小值是2014.
故选:A.
13.
【分析】本题考查了完全平方公式,整式的加减,先根据完全平方公式化简,再去括号合并同类项.
【详解】解:
.
故答案为:.
14. 16 4
【分析】本题考查完全平方公式,掌握完全平方公式是解题的关键.
(1)根据完全平方公式进行解答即可;
(2)根据完全平方公式进行解答即可.
【详解】解:(1);
(2).
故答案为:16;4;
15.(1)解:
;
(2)解:
;
(3)解:
.
题型04 完全平方公式在几何图形中的应用
16.A
【分析】本题考查了完全平方公式的几何背景的应用,根据题意列出阴影部分面积的表达式是解决本题的关键.
由图可得阴影部分面积为个直角三角形面积的和,用含、的式子表示出阴影部分的面积即可求解.
【详解】解:如图:
∵,,
∴,
∴,
,
∴,
解得:.
故选:A .
17.B
【分析】本题主要考查了完全平方式的知识,解决问题的关键是读懂题意,找到所求的量的等量关系.
由题意可得,则,再由可得,则,那么,从而求得答案.
【详解】解:由题意可得,
∴,
∵,
∴,
∴,
∴,
∴,
即长方形的面积是,
故选:B.
18.
【分析】用代数式分别表示图形中各个部分的面积,再根据各个部分面积之间的关系进行解答即可.
本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的关键.
【详解】解:整体上是边长为的正方形,
因此面积为,
拼成大正方形的9个部分的面积和为,
∴,
故答案为:.
19.4
【分析】本题考查了完全平方公式的应用,设这个正方形原来的边长为,则原来的面积就是,边长增加后的面积就是.根据“边长增加后的面积原来面积的9倍”即可列方程解答.
【详解】解:设正方形原来边长为,根据题意得:
,
,
,
解得,
即这个正方形原来的边长为.
故答案为:4.
20.解:(1)由图2可得小正方形(阴影部分)的边长为,
故答案为:;
(2)可得阴影部分面积为:,而阴影部分面积又可表示为,
∴,
∴;
(3)∵,,
∴;
(4)∵,
∴,
∴.
题型05 乘法公式的知二求三问题
21.(1)解:∵,
∴.
(2)解:∵,
∴.
22.(1),
;
(2),
.
23.解:因为,
所以,即.
因为,
所以,
所以.
24.(1)解:因为,,
所以,
所以,
所以;
(2)解:因为由(1)知,
又因为,,
所以
.
25.解:(1)∵,,
∴;
(2)∵,,
∴.
题型06 乘法公式中的整体带入方法
26.B
【分析】本题考查完全平方公式的应用,熟练掌握完全平方公式是解题的关键,根据题意巧妙构造,再利用完全平方公式展开,合并同类项后即可得到答案.
【详解】解:已知,
则,
那么,
整理得:,
则,
故选:B.
27.A
【分析】本题考查了完全平方公式,根据完全平方公式得到,再将代入即可求解,掌握相关知识是解题的关键.
【详解】解:
,
∵,
∴原式,
故选:A.
28.36
【分析】本题考查完全平方公式的几何背景,用不同的代数式表示阴影部分的面积是解决问题的关键.设a=x-2021,b=x-2023,进而得出则,再进行计算即可.
【详解】解:设,则,
所以,
即,
所以,
即.
故答案为:36
29.0或
【分析】本题主要考查了分式的求值,完全平方公式的变形求解,利用分类讨论的思想求解是解题的关键.当时和时,分别代入化简计算,即可作答.
【详解】解:,
或.
当时,;
当时,即,
,
,
,
,
故答案为:或.
30.(1)解:设,,
则,,
所以.
故答案为:30,20,340;
(2)解:设,,
则,,
,
,
,即
.
题型07 运用乘法公式解决规律性问题
31.D
【分析】本题考查了多项式乘多项式,数字类规律问题.先将变形为,根据求出的结果得出规律,即可解答.
【详解】解:
,
.
故选:D.
32.B
【分析】本题通过阅读理解寻找规律,观察已知给出的各式中的所有系数的和可得:(a+b)n(n为非负整数)展开式的各项系数和是2n,问题即得解决.
【详解】解:(a+b)0的展开式的各项系数和为:1=20;
(a+b)1的展开式的各项系数和为:1+1=2=21;
(a+b)2的展开式的各项系数和为:1+2+1=4=22;
(a+b)3的展开式的各项系数和为:1+3+3+1=8=23;
(a+b)4的展开式的各项系数和为:1+4+6+4+1=16=24;
……
∴(a+b)n(n为非负整数)的展开式的各项系数和为:2n.
∴(a+b)9的展开式中所有系数的和是:29=512.
故选:B.
33.
【分析】根据前面的变化规律,计算后解答即可.
【详解】∵
∴.
故答案为:.
34.(1)解:第5个等式为:,
故答案为:;
(2)解:第n个等式为:,
证明:左边,
右边,
左边右边,
等式成立.
35.解:①;
②;
③
.
题型08 乘法公式的新定义问题
36.A
【分析】本题考查了完全平方公式,解题的关键是读懂题意,掌握运算法则.根据完全平方公式,得,,再逐项判断即可.
【详解】解:由完全平方公式,得,,
若,则,,则;
若,则,,
∴和不一定相等,故A错误,B正确;
若,则,
又∵,,
∴,
∴;故C正确,不符合题意;
若,则或,则,故D正确,不符合题意.
故选A.
37.C
【分析】本题考查了整式的混合运算,根据题目中给出的定义利用完全平方公式化简计算即可.
【详解】解:,
,
故选:C.
38.5
【分析】本题考查了平方差公式和代数式求值,解题的关键是根据新定义运算法则得到关于x的等式.根据新运算的定义列出等式,然后再形求解即可.
【详解】解:由题意得:,
整理得:,
.
故答案为:5.
39.
【分析】本题主要考查平方差公式,解题的关键是理解题意;由题意可先求出的值,然后问题可求解.
【详解】解:∵,
∴,
∴;
故答案为.
40.(1)解:,
∴20是“妙数”;
故答案为:是;
(2)解:,理由如下:
.
为“妙数”,
,
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
