浙教版七年级下册 1.3 平行线 课件(共18张PPT)
文档属性
| 名称 | 浙教版七年级下册 1.3 平行线 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 10:21:22 | ||
图片预览



文档简介
(共18张PPT)
任何问题都可以转化为数学问题。
1.3 平行线
引入新知
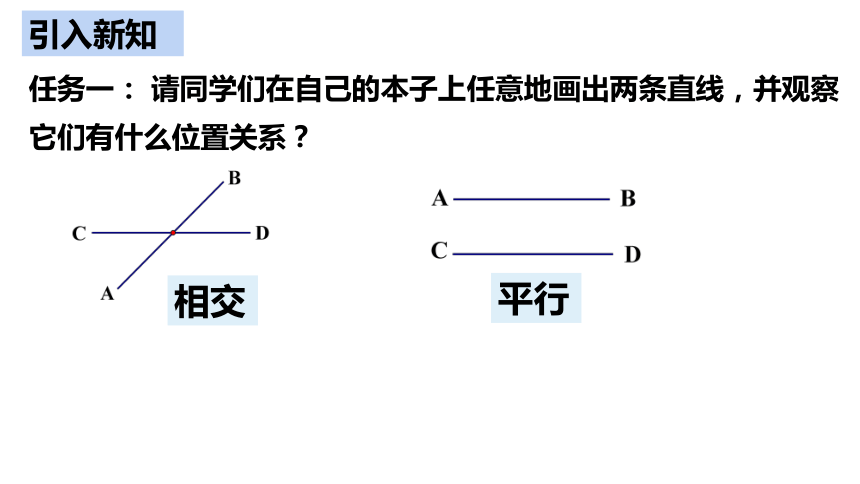
任务一: 请同学们在自己的本子上任意地画出两条直线,并观察它们有什么位置关系?
相交
平行
任务二你能说出生活中一些具有平行线形象的实际例子吗?
一.引入新知
下列说法对吗?“不相交的两条直线是平行线”
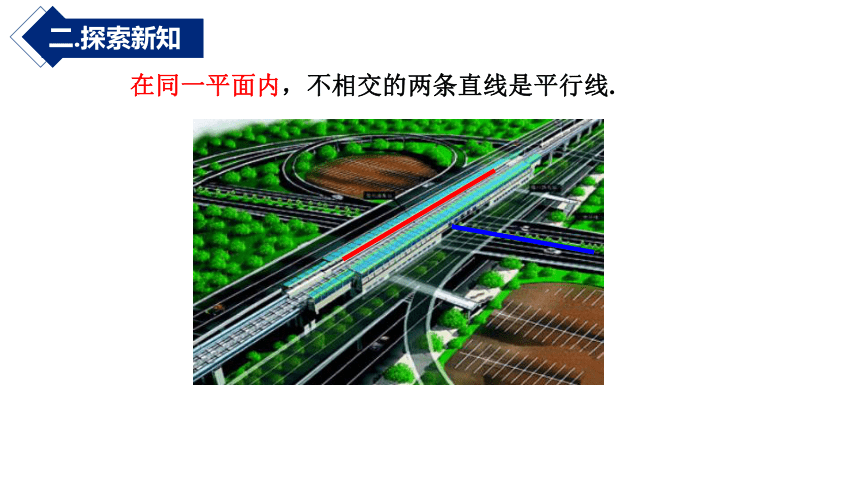
在同一平面内,不相交的两条直线是平行线.
二.探索新知
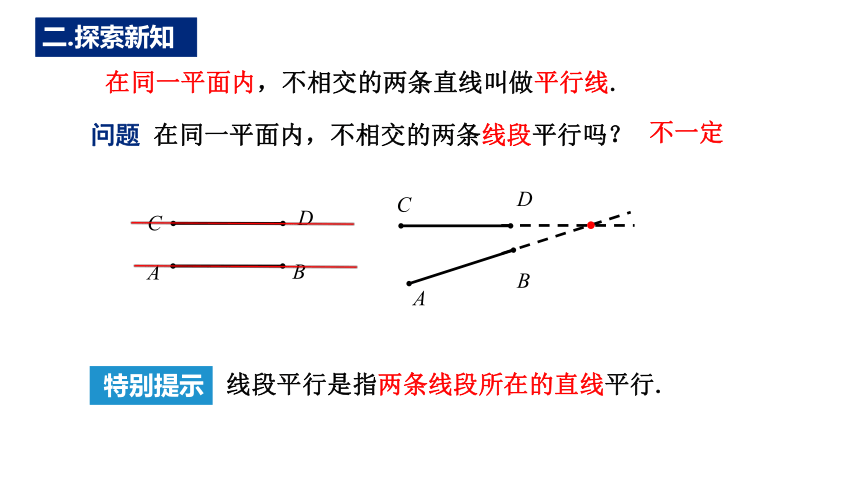
线段平行是指两条线段所在的直线平行.
二.探索新知
不一定
问题 在同一平面内,不相交的两条线段平行吗?
A
B
C
D
A
B
C
D
特别提示
在同一平面内,不相交的两条直线叫做平行线.
“平行”用“∥”表示.
如图,直线AB和CD是平行线,
二.探索新知
记做 AB∥CD(或 CD∥AB) ,
读做 直线 AB平行直线CD(或 直线AB与直线CD平行) .
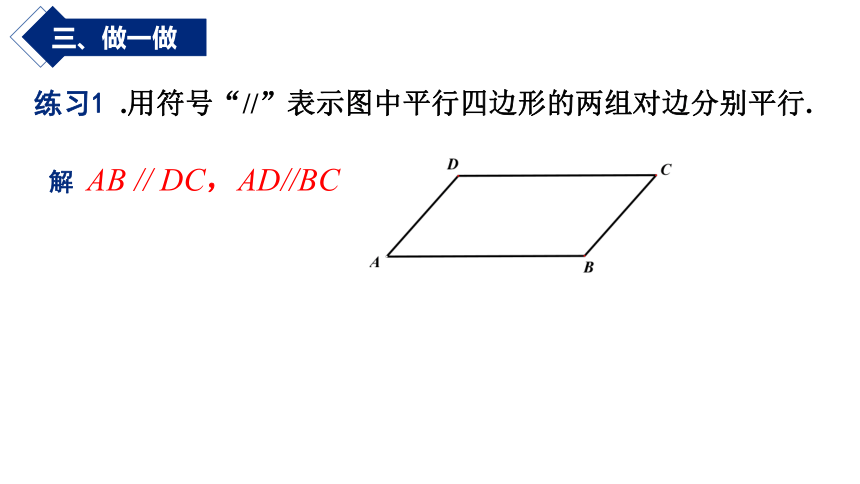
练习1 .用符号“//”表示图中平行四边形的两组对边分别平行.
解 AB // DC,AD//BC
三、做一做
A
D
C
B
A'
B'
D'
C'
和AB平行的棱有哪几条 (请用符号将它们表示出来)
2.一个长方体如图,和 平行的棱有哪几条?
答:和AA'平行的棱有3条:
BB'∥AA',
CC'∥AA',
DD'∥AA'.
和AB平行的棱有3条:
A'B'∥AB,
C'D'∥AB,
CD∥AB.
三、做一做
用三角尺和直尺画直线b和已知直线 平行.请按图示方法画一画,你能概括出这种画法的基本步骤吗?
二靠:
三角尺的一边和直尺紧靠一起;
三推:
推动三角尺;
四画:
画出直线 .
一放:
使三角尺的一边放在已知直线 上;
四.自主学习
无数条
议一议 画已知直线的平行线可以画多少条?
四.自主学习
l
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
1.放
2.靠
3.推
4.画
P
议一议 过已知直线外一点画已知直线的平行线可以画多少条
l
一条
四.自主学习
基本事实:
过直线外一点,有且仅有一条直线与已知直线平行。
B
A
如图,点M,N代表两个城市,MA,MB是已建的两条公路。现规划建造两条经N市的公路,这两条路分别与MA,MB平行,并在与MB,MA的交汇处分别建一座立交桥,问立交桥应建在何处?请画出示意图。
M
N
Q
P
答:立交桥应分别建在P,Q处.
(1)直线NP、NQ的位置是唯一的吗?为什么?
(2)点P、点Q的位置是唯一的吗?为什么?
五、应用新知
五.应用新知
练习1 如图,AB,BC是一个平行四边形相邻的两边.请把这个平行四边形补画完整.
变式 如图,A,B,C是一个平行四边形的三个顶点,请画出所有满足题意的平行四边形,并用符号“//”表示图中的平行线.
解 AB//DF,
BC//ED,
AC//EF.
五.应用新知
练习2 我们把如图图形叫做2×2斜方格,它由四个边长都为1cm,其中较小内角为45 的平行四边形组成.请你画一个3×3斜方格.
五.应用新知
六.拓展提升
练习3 (1)同一平面内的两条直线有几个交点?
0个或1个
练习5 (2)同一平面内的三条直线有几个交点?
七.拓展
0个或1个或2个或3个
八.总结
平行线的画法
画
推
靠
放
基本事实:经过直线外一点,有且仅有一条直线与这条直线平行.
实际应用
问题1:你能说出平行线的画法吗?
问题2:你能说出平行线的基本事实吗?
任何问题都可以转化为数学问题。
1.3 平行线
引入新知
任务一: 请同学们在自己的本子上任意地画出两条直线,并观察它们有什么位置关系?
相交
平行
任务二你能说出生活中一些具有平行线形象的实际例子吗?
一.引入新知
下列说法对吗?“不相交的两条直线是平行线”
在同一平面内,不相交的两条直线是平行线.
二.探索新知
线段平行是指两条线段所在的直线平行.
二.探索新知
不一定
问题 在同一平面内,不相交的两条线段平行吗?
A
B
C
D
A
B
C
D
特别提示
在同一平面内,不相交的两条直线叫做平行线.
“平行”用“∥”表示.
如图,直线AB和CD是平行线,
二.探索新知
记做 AB∥CD(或 CD∥AB) ,
读做 直线 AB平行直线CD(或 直线AB与直线CD平行) .
练习1 .用符号“//”表示图中平行四边形的两组对边分别平行.
解 AB // DC,AD//BC
三、做一做
A
D
C
B
A'
B'
D'
C'
和AB平行的棱有哪几条 (请用符号将它们表示出来)
2.一个长方体如图,和 平行的棱有哪几条?
答:和AA'平行的棱有3条:
BB'∥AA',
CC'∥AA',
DD'∥AA'.
和AB平行的棱有3条:
A'B'∥AB,
C'D'∥AB,
CD∥AB.
三、做一做
用三角尺和直尺画直线b和已知直线 平行.请按图示方法画一画,你能概括出这种画法的基本步骤吗?
二靠:
三角尺的一边和直尺紧靠一起;
三推:
推动三角尺;
四画:
画出直线 .
一放:
使三角尺的一边放在已知直线 上;
四.自主学习
无数条
议一议 画已知直线的平行线可以画多少条?
四.自主学习
l
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
1.放
2.靠
3.推
4.画
P
议一议 过已知直线外一点画已知直线的平行线可以画多少条
l
一条
四.自主学习
基本事实:
过直线外一点,有且仅有一条直线与已知直线平行。
B
A
如图,点M,N代表两个城市,MA,MB是已建的两条公路。现规划建造两条经N市的公路,这两条路分别与MA,MB平行,并在与MB,MA的交汇处分别建一座立交桥,问立交桥应建在何处?请画出示意图。
M
N
Q
P
答:立交桥应分别建在P,Q处.
(1)直线NP、NQ的位置是唯一的吗?为什么?
(2)点P、点Q的位置是唯一的吗?为什么?
五、应用新知
五.应用新知
练习1 如图,AB,BC是一个平行四边形相邻的两边.请把这个平行四边形补画完整.
变式 如图,A,B,C是一个平行四边形的三个顶点,请画出所有满足题意的平行四边形,并用符号“//”表示图中的平行线.
解 AB//DF,
BC//ED,
AC//EF.
五.应用新知
练习2 我们把如图图形叫做2×2斜方格,它由四个边长都为1cm,其中较小内角为45 的平行四边形组成.请你画一个3×3斜方格.
五.应用新知
六.拓展提升
练习3 (1)同一平面内的两条直线有几个交点?
0个或1个
练习5 (2)同一平面内的三条直线有几个交点?
七.拓展
0个或1个或2个或3个
八.总结
平行线的画法
画
推
靠
放
基本事实:经过直线外一点,有且仅有一条直线与这条直线平行.
实际应用
问题1:你能说出平行线的画法吗?
问题2:你能说出平行线的基本事实吗?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
