浙教版七年级下册 1.3 平行线 课件(共32张PPT)
文档属性
| 名称 | 浙教版七年级下册 1.3 平行线 课件(共32张PPT) | 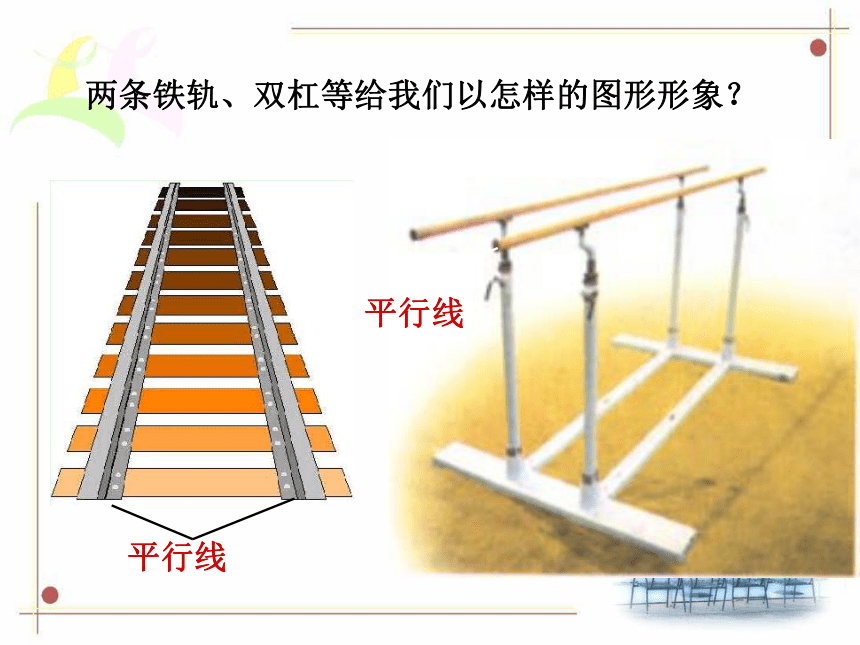 | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-11 10:20:21 | ||
图片预览







文档简介
(共32张PPT)
两条铁轨、双杠等给我们以怎样的图形形象?
平行线
平行线
走廊通道
橱柜
教室黑板
窗框
我们的教室有哪些实物给人以平行线的现象?
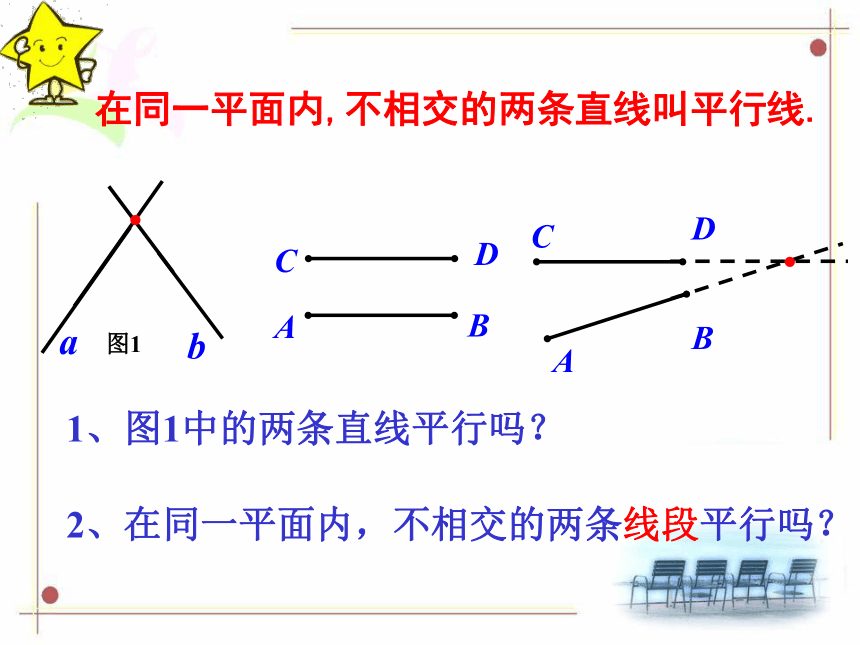
你能给平行线下个定义吗
在同一平面内,不相交的两条直线叫平行线.
a
b
1、图1中的两条直线平行吗?
在同一平面内,不相交的两条直线叫平行线.
图1
2、在同一平面内,不相交的两条线段平行吗?
A
B
C
D
A
B
C
D
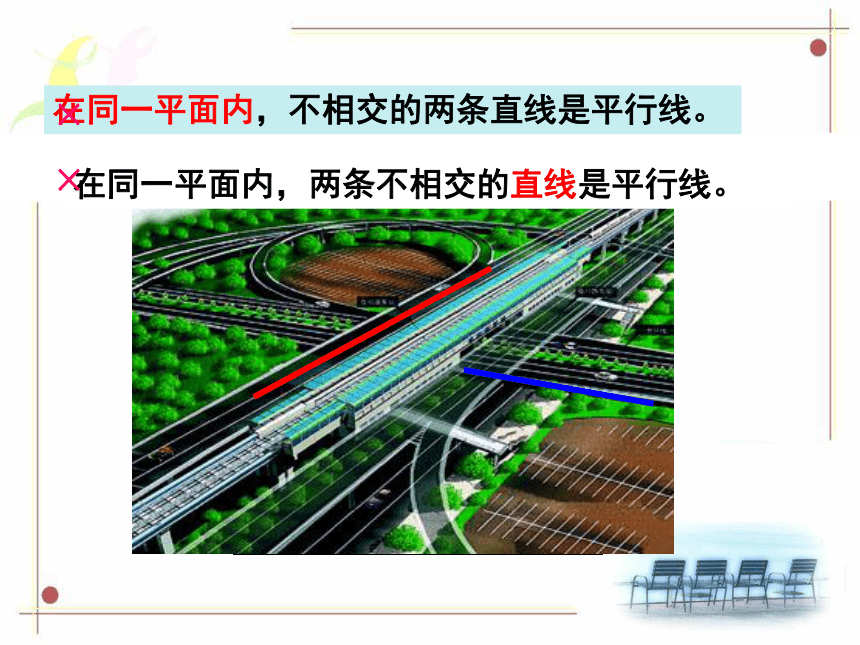
①不相交的两条直线是平行线。
在同一平面内,不相交的两条直线是平行线。
②在同一平面内,两条不相交的线段是平行线。
在同一平面内,两条不相交的直线是平行线。
×
×
3.平行线指的是直线,而不是射线或线段。线段的平行是指两条线段所在直线的平行。
特别提示:
1.“在同一平面内”是前提条件
在同一平面内,不相交的两条直线叫做平行线。
2.“不相交”是指没有交点
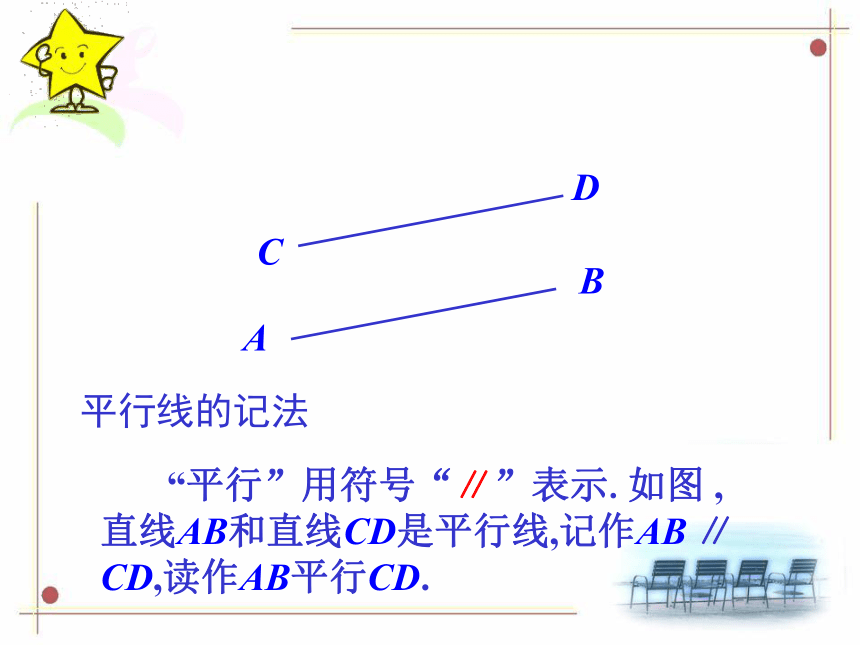
“平行”用符号“∥”表示.如图 ,直线AB和直线CD是平行线,记作AB ∥ CD,读作AB平行CD.
A
B
C
D
平行线的记法
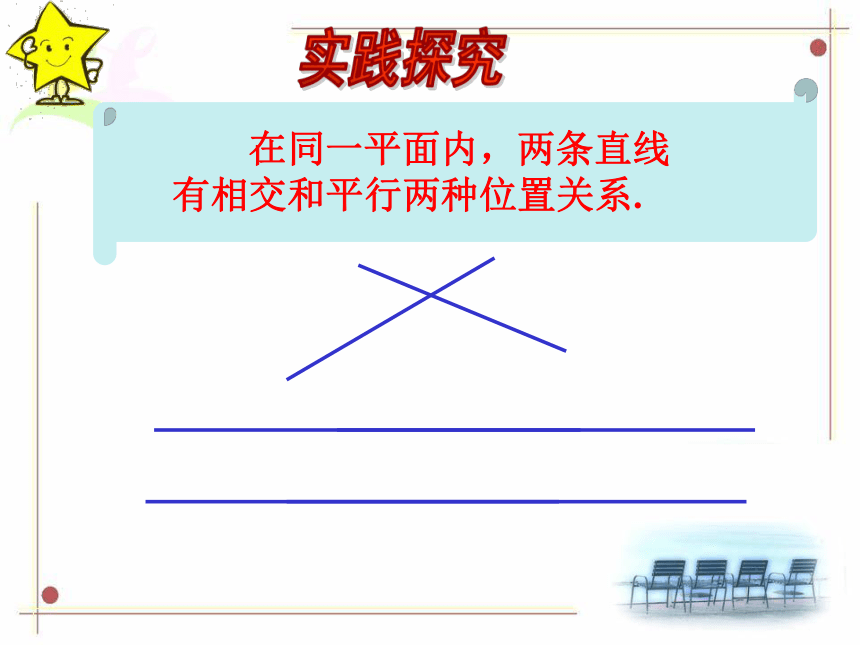
如果一个平面内有两条直线,那么这两条直线会有怎样的位置关系呢?
在同一平面内,两条直线
有相交和平行两种位置关系.
( )
1. 不相交的两条直线叫做平行线.( )
×
2. 在同一平面内,两条不平行的直线必相交 . ( )
√
3.在同一平面内两 条直线的位置只有平行、相交.( )
√
4.在同一平面内不相交的两条线段必平行
×
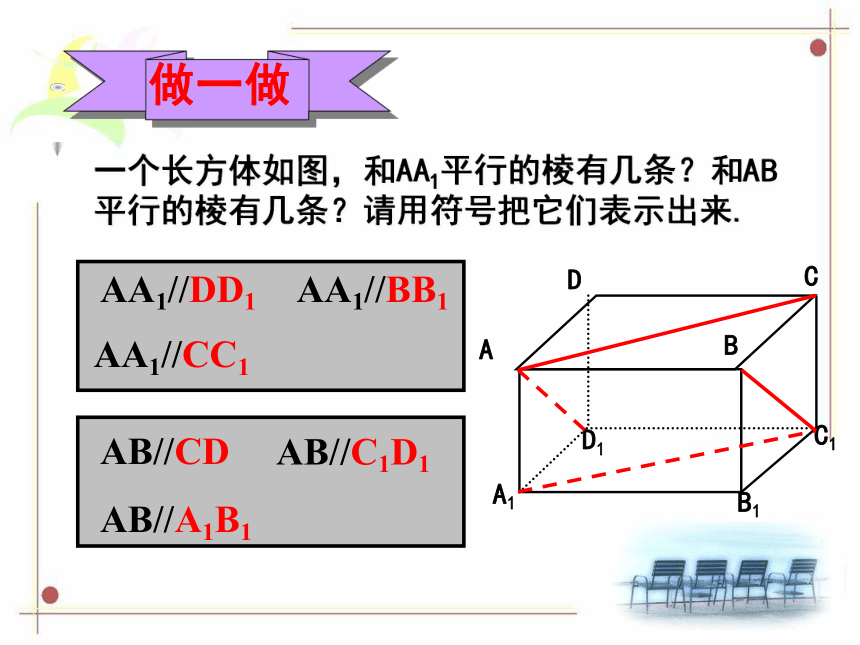
一个长方体如图,和AA1平行的棱有几条?和AB平行的棱有几条?请用符号把它们表示出来.
A
B
D
C
A1
D1
B1
C1
AA1//DD1
AA1//CC1
AA1//BB1
AB//CD
AB//C1D1
AB//A1B1
做一做
利用横线画
利用竖线画
利用对角线画
你能利用方格纸画平行线吗?比一比,看谁的方法多.
画法一
思考:平时你是怎样画长方形的?
B
A
C
D
你能利用长方形的特点画出AB的平行线吗?
B
A
你能利用长方形的特点画出AB的平行线吗?
B
A
画法:
1、任意画一条直线CD,使CD ⊥AB.
C
D
你能利用刚才的方法画出AB的平行线吗?
B
A
画法:
1、任意画一条直线CD,使CD ⊥AB.
2、画直线EF,使EF ⊥ CD.
C
D
你能利用刚才的方法画出AB的平行线吗?
B
A
E
F
利用垂线画平行线
画法:
1、任意画一条直线CD,使CD ⊥AB.
2、画直线EF,使EF ⊥ CD.
C
D
则PQ AB,PQ就是所要画的直线 。
∥
画法二: (如图)
1.任意画一条直线 ,使
2.过点P画直线PQ
A
B
P
Q
你会画平行线吗?
一、放
二、靠
三、推
四、画
画法三:
●
能画几条直线和已知直线AB平行呢
无数条
画直线AB的平行线,我们能画出几条?
B
A
过直线外一点P,平行AB的直线有几条?
P
你能归纳出平行线的这一基本性质吗?
B
A
经过直线外一点,有且只有一条直线
与已知直线平行.
P
过直线外一点P,平行AB的直线有几条?
平行公理
(1)经过点A画出直线n的平行线,能画几条?
(2)过点B画一条直线与直线n平行,它与(1)中所画的直线平行吗?
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
·
·
A
B
n
平行线的传递性 (平行公理的推论):
结论:
几何语言表达式:∵a∥n m∥n(已知)
∴a∥m (平行线的传递性)
m
a
探究新知
B
A
例题:如图,点M,N代表两个城市,MA,MB是已建的两条公路。现规划建造两条经N市的公路,这两条路分别与MA,MB平行,并在与MB,MA的交汇处分别建一座立交桥,问立交桥应建在何处?请画出示意图。
M
N
Q
P
解:如图P、Q为所求
1、在同一个平面内, 的两条直线叫做平行线.
则在同一个平面内两条直线的位置关系是 .
不相交
课内练习
相交或平行
2 、用符号“∥”表示图中平行四边形的两组对边分别平行。
A
B
C
D
AB∥ CD,AD∥ BC。
3 、如图,在 ΔABC中,P是AC边上一点,过点P分别画AB,BC的平行线。
·P
A
B
C
请找出图中各对相互平行线,并用符号表示出来。
A
B
D
C
E
H
G
O
P
F
归纳小结
只有一个公共点的两条直线
同一个平面内不相交的两条直线
a
b
O
直线a 、b交于O
a
b
a //b
对顶角相等
平行公理
邻补角互补
平行公理推论:
∵ a ∥ c,b ∥ c ; ∴ a ∥ b
b
a
c
你学会了吗
请谈谈这节课你的收获.
1、平行线的概念:
3、平行线的基本性质:
2、平行线的画法:
经过直线外一点,有且只有一条直线与已知直线平行.
在同一平面内,不相交的两条直线叫平行线.
(2)利用垂线画平行线
(3)推平行线法(放,靠,推,画).
(1)利用方格子画平行线
如图A、B、C是三棵树,藏宝的地点D与这三棵树构成一个平行四边形,你能确定藏宝的地点吗?请画一画.
A
B
C
拓展练习(一)
0个交点
1个交点
2个交点
3个交点
同一平面内互不重合的三条直线的交点个数可能是__________________________ _。
0 个,1 个,2 个或 3 个
拓展练习(二)
1、平面内有若干条直线,当下列情形时,交点个数最多有几个?
2条
3条
10条
…
…
n条
(1)有2条直线时,交点个数最多是: 1 个。
(2)有3条直线时,交点个数最多是: 个。
(3)有4条直线时,交点个数最多是: 个。
(4)有10条直线时,交点个数最多是: 个。
……
(5)有n条直线时,交点个数最多是: 个。
4条
3
6
?
10(10-1)÷2=45
45
拓展练习(三)
两条铁轨、双杠等给我们以怎样的图形形象?
平行线
平行线
走廊通道
橱柜
教室黑板
窗框
我们的教室有哪些实物给人以平行线的现象?
你能给平行线下个定义吗
在同一平面内,不相交的两条直线叫平行线.
a
b
1、图1中的两条直线平行吗?
在同一平面内,不相交的两条直线叫平行线.
图1
2、在同一平面内,不相交的两条线段平行吗?
A
B
C
D
A
B
C
D
①不相交的两条直线是平行线。
在同一平面内,不相交的两条直线是平行线。
②在同一平面内,两条不相交的线段是平行线。
在同一平面内,两条不相交的直线是平行线。
×
×
3.平行线指的是直线,而不是射线或线段。线段的平行是指两条线段所在直线的平行。
特别提示:
1.“在同一平面内”是前提条件
在同一平面内,不相交的两条直线叫做平行线。
2.“不相交”是指没有交点
“平行”用符号“∥”表示.如图 ,直线AB和直线CD是平行线,记作AB ∥ CD,读作AB平行CD.
A
B
C
D
平行线的记法
如果一个平面内有两条直线,那么这两条直线会有怎样的位置关系呢?
在同一平面内,两条直线
有相交和平行两种位置关系.
( )
1. 不相交的两条直线叫做平行线.( )
×
2. 在同一平面内,两条不平行的直线必相交 . ( )
√
3.在同一平面内两 条直线的位置只有平行、相交.( )
√
4.在同一平面内不相交的两条线段必平行
×
一个长方体如图,和AA1平行的棱有几条?和AB平行的棱有几条?请用符号把它们表示出来.
A
B
D
C
A1
D1
B1
C1
AA1//DD1
AA1//CC1
AA1//BB1
AB//CD
AB//C1D1
AB//A1B1
做一做
利用横线画
利用竖线画
利用对角线画
你能利用方格纸画平行线吗?比一比,看谁的方法多.
画法一
思考:平时你是怎样画长方形的?
B
A
C
D
你能利用长方形的特点画出AB的平行线吗?
B
A
你能利用长方形的特点画出AB的平行线吗?
B
A
画法:
1、任意画一条直线CD,使CD ⊥AB.
C
D
你能利用刚才的方法画出AB的平行线吗?
B
A
画法:
1、任意画一条直线CD,使CD ⊥AB.
2、画直线EF,使EF ⊥ CD.
C
D
你能利用刚才的方法画出AB的平行线吗?
B
A
E
F
利用垂线画平行线
画法:
1、任意画一条直线CD,使CD ⊥AB.
2、画直线EF,使EF ⊥ CD.
C
D
则PQ AB,PQ就是所要画的直线 。
∥
画法二: (如图)
1.任意画一条直线 ,使
2.过点P画直线PQ
A
B
P
Q
你会画平行线吗?
一、放
二、靠
三、推
四、画
画法三:
●
能画几条直线和已知直线AB平行呢
无数条
画直线AB的平行线,我们能画出几条?
B
A
过直线外一点P,平行AB的直线有几条?
P
你能归纳出平行线的这一基本性质吗?
B
A
经过直线外一点,有且只有一条直线
与已知直线平行.
P
过直线外一点P,平行AB的直线有几条?
平行公理
(1)经过点A画出直线n的平行线,能画几条?
(2)过点B画一条直线与直线n平行,它与(1)中所画的直线平行吗?
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
·
·
A
B
n
平行线的传递性 (平行公理的推论):
结论:
几何语言表达式:∵a∥n m∥n(已知)
∴a∥m (平行线的传递性)
m
a
探究新知
B
A
例题:如图,点M,N代表两个城市,MA,MB是已建的两条公路。现规划建造两条经N市的公路,这两条路分别与MA,MB平行,并在与MB,MA的交汇处分别建一座立交桥,问立交桥应建在何处?请画出示意图。
M
N
Q
P
解:如图P、Q为所求
1、在同一个平面内, 的两条直线叫做平行线.
则在同一个平面内两条直线的位置关系是 .
不相交
课内练习
相交或平行
2 、用符号“∥”表示图中平行四边形的两组对边分别平行。
A
B
C
D
AB∥ CD,AD∥ BC。
3 、如图,在 ΔABC中,P是AC边上一点,过点P分别画AB,BC的平行线。
·P
A
B
C
请找出图中各对相互平行线,并用符号表示出来。
A
B
D
C
E
H
G
O
P
F
归纳小结
只有一个公共点的两条直线
同一个平面内不相交的两条直线
a
b
O
直线a 、b交于O
a
b
a //b
对顶角相等
平行公理
邻补角互补
平行公理推论:
∵ a ∥ c,b ∥ c ; ∴ a ∥ b
b
a
c
你学会了吗
请谈谈这节课你的收获.
1、平行线的概念:
3、平行线的基本性质:
2、平行线的画法:
经过直线外一点,有且只有一条直线与已知直线平行.
在同一平面内,不相交的两条直线叫平行线.
(2)利用垂线画平行线
(3)推平行线法(放,靠,推,画).
(1)利用方格子画平行线
如图A、B、C是三棵树,藏宝的地点D与这三棵树构成一个平行四边形,你能确定藏宝的地点吗?请画一画.
A
B
C
拓展练习(一)
0个交点
1个交点
2个交点
3个交点
同一平面内互不重合的三条直线的交点个数可能是__________________________ _。
0 个,1 个,2 个或 3 个
拓展练习(二)
1、平面内有若干条直线,当下列情形时,交点个数最多有几个?
2条
3条
10条
…
…
n条
(1)有2条直线时,交点个数最多是: 1 个。
(2)有3条直线时,交点个数最多是: 个。
(3)有4条直线时,交点个数最多是: 个。
(4)有10条直线时,交点个数最多是: 个。
……
(5)有n条直线时,交点个数最多是: 个。
4条
3
6
?
10(10-1)÷2=45
45
拓展练习(三)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
