1.2 同位角、内错角、同旁内角 同步练习(含答案)
文档属性
| 名称 | 1.2 同位角、内错角、同旁内角 同步练习(含答案) | 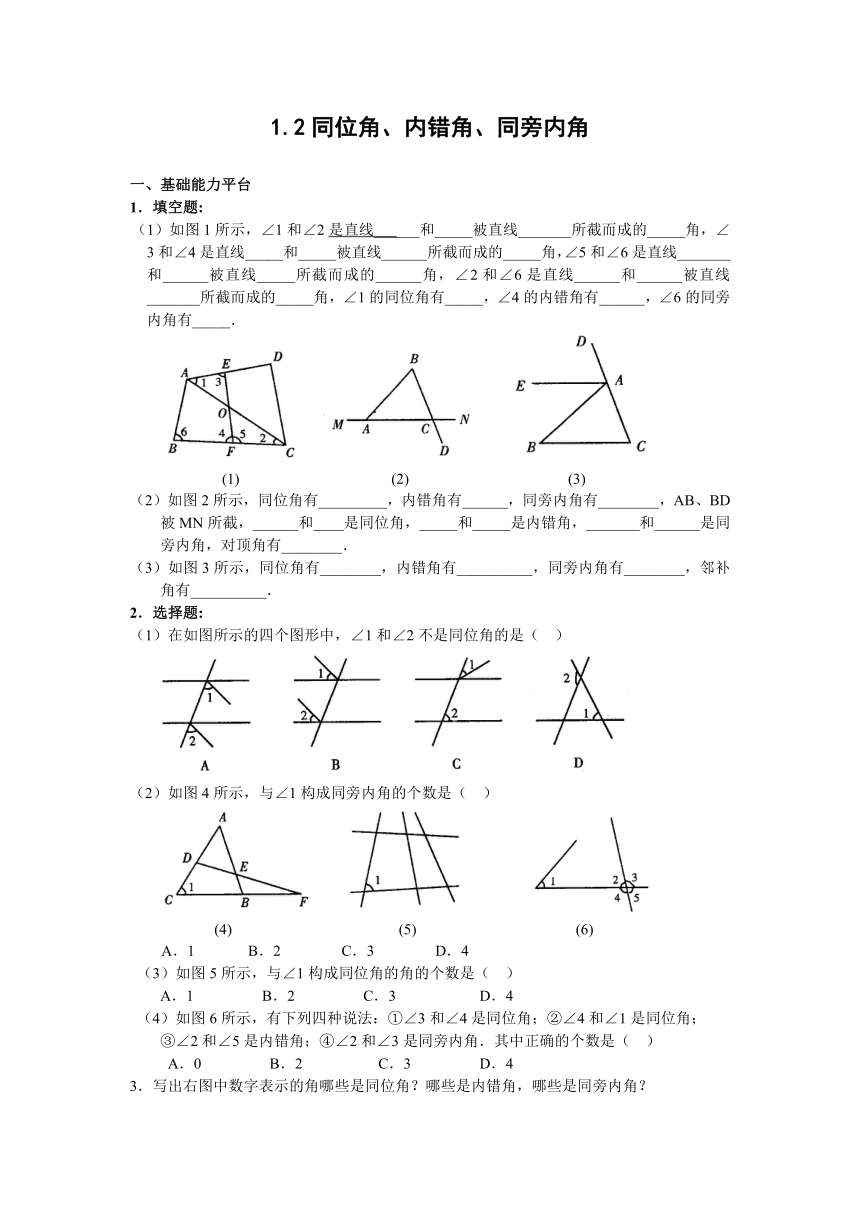 | |
| 格式 | zip | ||
| 文件大小 | 39.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-30 15:37:51 | ||
图片预览

文档简介
1.2同位角、内错角、同旁内角
一、基础能力平台
1.填空题:
(1)如图1所示,∠1和∠2是直线___
( http: / / www.21cnjy.com )___和_____被直线_______所截而成的_____角,∠3和∠4是直线_____和_____被直线______所截而成的_____角,∠5和∠6是直线_______和______被直线_____所截而成的______角,∠2和∠6是直线______和______被直线_______所截而成的_____角,∠1的同位角有_____,∠4的内错角有______,∠6的同旁内角有_____.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)
(2)
(3)
(2)如图2所示,同位角有_________,内错角有______,同旁内角有________,AB、BD被MN所截,______和____是同位角,_____和_____是内错角,_______和______是同旁内角,对顶角有________.
(3)如图3所示,同位角有________,内错角有__________,同旁内角有________,邻补角有__________.
2.选择题:
(1)在如图所示的四个图形中,∠1和∠2不是同位角的是(
)
( http: / / www.21cnjy.com )
(2)如图4所示,与∠1构成同旁内角的个数是(
)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(4)
(5)
(6)
A.1
B.2
C.3
D.4
(3)如图5所示,与∠1构成同位角的角的个数是(
)
A.1
B.2
C.3
D.4
(4)如图6所示,有下列四种说法:①∠3和∠4是同位角;②∠4和∠1是同位角;
③∠2和∠5是内错角;④∠2和∠3是同旁内角.其中正确的个数是(
)
A.0
B.2
C.3
D.4
3.写出右图中数字表示的角哪些是同位角?哪些是内错角,哪些是同旁内角?
( http: / / www.21cnjy.com )
4.在括号中填写理由.
如图所示,
因为∠2=∠4(______________),
又因为∠1=∠4(已知),
所以∠2=∠1(_________________________).
因为∠3与∠4互为邻补角(邻补角定义),
所以∠3+∠4=180°(____________________________).
所以∠3+∠1=180°(___________________________).
所以∠3与∠1互为补角(_______________________).
5.找出下图中所有的同位角、内错角、同旁内角.
( http: / / www.21cnjy.com )
二、拓展延伸训练
如图所示,指出下列各组角是由哪两条直线被哪
( http: / / www.21cnjy.com )一条直线所截得的,并说出它们是什么角,∠1和∠2,∠2和∠6,∠6和∠A,∠A和∠7,∠3和∠5,∠3和∠4,∠4和∠7.
( http: / / www.21cnjy.com )
三、自主探究提高
作出一个共有两组同位角,两组内错角,四组同旁内角的图形,并指出图中的同位角、内错角和同旁内角.
答案:
【基础能力平台】
1.(1)AD
BC
AC
内错
AD
BC
EF
同旁内
AB
EF
BC
同位
AB
AC
BC
同旁内
∠OED,∠EOC
∠FOC,∠FED
∠4,∠2,∠BAC,∠BAD,∠BCD
(2)∠BAM与∠BCM,∠BAC与∠
( http: / / www.21cnjy.com )BCN,∠B和∠ACD
∠B和∠BCN,∠B和∠BAM,∠BAC和∠ACD
∠B和∠BAC,∠B和∠BCA,∠BAC和∠BCA
∠BAC和∠BCN或∠BAM和∠BCA
∠BAC和∠ACD
∠BAC和∠BCA
∠ACD和∠BCN,∠BCA和∠DCN
(3)∠C和∠DAE,∠C和∠DA
( http: / / www.21cnjy.com )B
∠EAB和∠B,∠B和∠BAD
∠B和∠BAC,∠B和∠C,∠C和∠CAB,∠C和∠EAC
∠DAE和∠EAC,∠DAB和∠BAC
2.(1)B
(2)D
(3)C
(4)A
3.在图中,同位角有∠1和∠3,∠5和∠6,内错角有∠2和∠4,∠1和∠6
同旁内角有∠1和∠5,∠2和∠6,∠3和∠4,∠3和∠5
4.对顶角相等
等量代换
邻补角定义
等量代换
被角定义
5.略
【拓展延伸训练】略
【自主探究提高】略
一、基础能力平台
1.填空题:
(1)如图1所示,∠1和∠2是直线___
( http: / / www.21cnjy.com )___和_____被直线_______所截而成的_____角,∠3和∠4是直线_____和_____被直线______所截而成的_____角,∠5和∠6是直线_______和______被直线_____所截而成的______角,∠2和∠6是直线______和______被直线_______所截而成的_____角,∠1的同位角有_____,∠4的内错角有______,∠6的同旁内角有_____.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)
(2)
(3)
(2)如图2所示,同位角有_________,内错角有______,同旁内角有________,AB、BD被MN所截,______和____是同位角,_____和_____是内错角,_______和______是同旁内角,对顶角有________.
(3)如图3所示,同位角有________,内错角有__________,同旁内角有________,邻补角有__________.
2.选择题:
(1)在如图所示的四个图形中,∠1和∠2不是同位角的是(
)
( http: / / www.21cnjy.com )
(2)如图4所示,与∠1构成同旁内角的个数是(
)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(4)
(5)
(6)
A.1
B.2
C.3
D.4
(3)如图5所示,与∠1构成同位角的角的个数是(
)
A.1
B.2
C.3
D.4
(4)如图6所示,有下列四种说法:①∠3和∠4是同位角;②∠4和∠1是同位角;
③∠2和∠5是内错角;④∠2和∠3是同旁内角.其中正确的个数是(
)
A.0
B.2
C.3
D.4
3.写出右图中数字表示的角哪些是同位角?哪些是内错角,哪些是同旁内角?
( http: / / www.21cnjy.com )
4.在括号中填写理由.
如图所示,
因为∠2=∠4(______________),
又因为∠1=∠4(已知),
所以∠2=∠1(_________________________).
因为∠3与∠4互为邻补角(邻补角定义),
所以∠3+∠4=180°(____________________________).
所以∠3+∠1=180°(___________________________).
所以∠3与∠1互为补角(_______________________).
5.找出下图中所有的同位角、内错角、同旁内角.
( http: / / www.21cnjy.com )
二、拓展延伸训练
如图所示,指出下列各组角是由哪两条直线被哪
( http: / / www.21cnjy.com )一条直线所截得的,并说出它们是什么角,∠1和∠2,∠2和∠6,∠6和∠A,∠A和∠7,∠3和∠5,∠3和∠4,∠4和∠7.
( http: / / www.21cnjy.com )
三、自主探究提高
作出一个共有两组同位角,两组内错角,四组同旁内角的图形,并指出图中的同位角、内错角和同旁内角.
答案:
【基础能力平台】
1.(1)AD
BC
AC
内错
AD
BC
EF
同旁内
AB
EF
BC
同位
AB
AC
BC
同旁内
∠OED,∠EOC
∠FOC,∠FED
∠4,∠2,∠BAC,∠BAD,∠BCD
(2)∠BAM与∠BCM,∠BAC与∠
( http: / / www.21cnjy.com )BCN,∠B和∠ACD
∠B和∠BCN,∠B和∠BAM,∠BAC和∠ACD
∠B和∠BAC,∠B和∠BCA,∠BAC和∠BCA
∠BAC和∠BCN或∠BAM和∠BCA
∠BAC和∠ACD
∠BAC和∠BCA
∠ACD和∠BCN,∠BCA和∠DCN
(3)∠C和∠DAE,∠C和∠DA
( http: / / www.21cnjy.com )B
∠EAB和∠B,∠B和∠BAD
∠B和∠BAC,∠B和∠C,∠C和∠CAB,∠C和∠EAC
∠DAE和∠EAC,∠DAB和∠BAC
2.(1)B
(2)D
(3)C
(4)A
3.在图中,同位角有∠1和∠3,∠5和∠6,内错角有∠2和∠4,∠1和∠6
同旁内角有∠1和∠5,∠2和∠6,∠3和∠4,∠3和∠5
4.对顶角相等
等量代换
邻补角定义
等量代换
被角定义
5.略
【拓展延伸训练】略
【自主探究提高】略
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
