1.4 平行线的性质 同步练习(含答案)
文档属性
| 名称 | 1.4 平行线的性质 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 41.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-30 15:38:49 | ||
图片预览

文档简介
1.3
平行线的性质
一、基础能力平台
1.选择题:
(1)下列说法中,不正确的是(
)
A.同位角相等,两直线平行;
B.两直线平行,内错角相等;
C.两直线被第三条直线所截,同旁内角互补;
D.同旁内角互补,两直线平行
(2)如图1所示,AC平分∠BCD,且∠BCA=∠CAD=∠CAB,∠ABC=75°,
则∠BCA等于(
)
A.36°
B.35°
C.
37.5°
D.70°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)
(2)
(3)
(3)如图2所示,AD⊥BC于D,DG∥AB,那么∠B和∠ADG的关系是(
)
A.互余
B.互补
C.相等
D.以上都不对
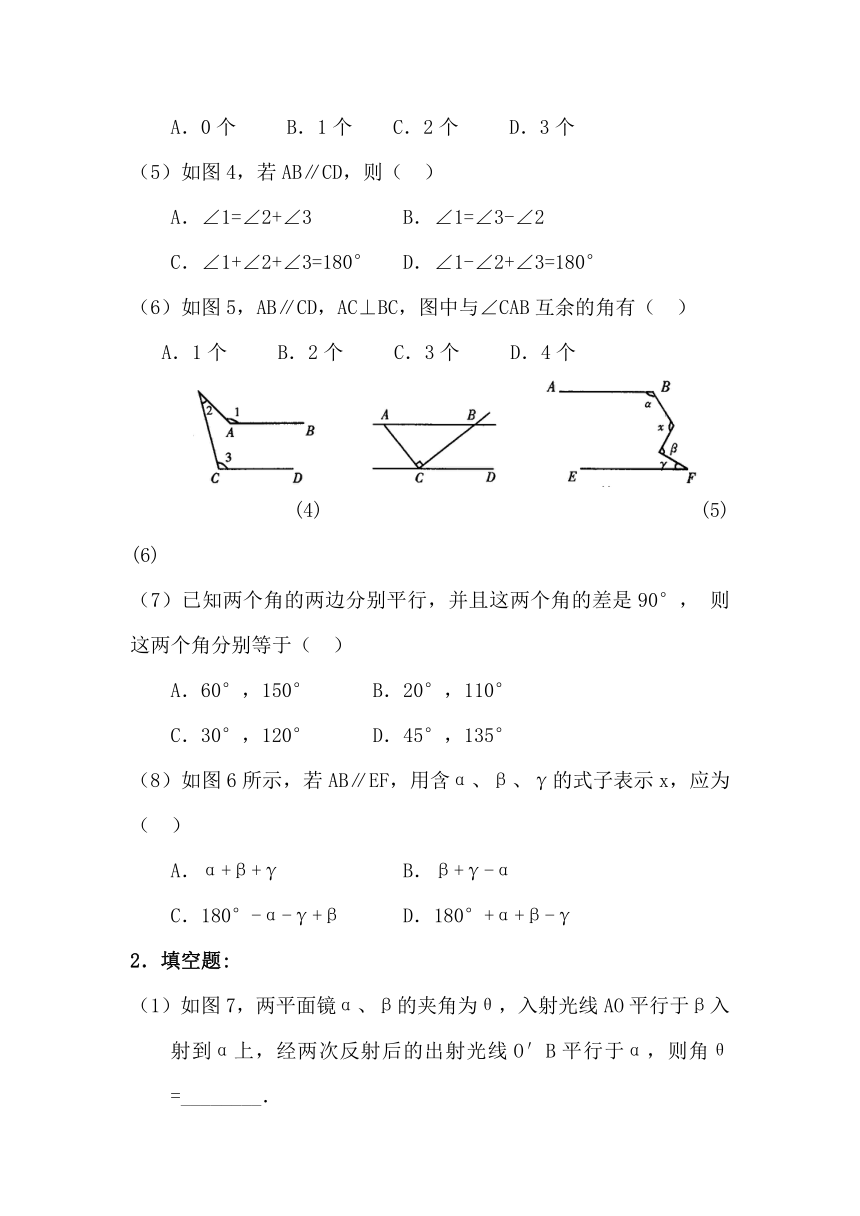
(4)如图3,直线c与直线a、b相交,且a∥b,则下列结论:
①∠1=∠2;②∠1=∠3;③∠3=∠2中,正确的个数为(
)
A.0个
B.1个
C.2个
D.3个
(5)如图4,若AB∥CD,则(
)
A.∠1=∠2+∠3
B.∠1=∠3-∠2
C.∠1+∠2+∠3=180°
D.∠1-∠2+∠3=180°
(6)如图5,AB∥CD,AC⊥BC,图中与∠CAB互余的角有(
)
A.1个
B.2个
C.3个
D.4个
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(4)
(5)
(6)
(7)已知两个角的两边分别平行,并且这两个角的差是90°,则这两个角分别等于(
)
A.60°,150°
B.20°,110°
C.30°,120°
D.45°,135°
(8)如图6所示,若AB∥EF,用含α、β、γ的式子表示x,应为(
)
A.α+β+γ
B.β+γ-α
C.180°-α-γ+β
D.180°+α+β-γ
2.填空题:
(1)如图7,两平面镜α、β的夹角为θ,入射光线AO平行于β入射到α上,经两次反射后的出射光线O′B平行于α,则角θ=________.
(2)如图8所示,直线a∥b,则∠A=_______.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(7)
(8)
(9)
3.填写理由:
(1)如图9所示,因为DF∥AC(已知),
所以∠D+______=180°(__________________________)
因为∠C=∠D(已知),
所以∠C+_______=180°(_________________________)
所以DB∥EC(_________).
(2)如图所示,因为∠A=∠BDE(已知),
所以______∥_____(__________________________)
所以∠DEB=_______(_________________________)
因为∠C=90°(已知),
所以∠DEB=______(_________________________)
所以DE⊥______(_________________________)
二、拓展延伸训练
1.如图所示,已知AD、BC相交于O,∠A=∠D,试说明一定有∠C=∠B.
( http: / / www.21cnjy.com )
2.如图所示,已知AB∥CD,AD∥BC,BF平分∠ABC,DE平分∠ADC,则一定有DE∥FB,它的根据是什么?
( http: / / www.21cnjy.com )
三、自主探究提高
如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
( http: / / www.21cnjy.com )
答案:
【基础能力平台】
1.(1)C
(2)B
(3)A
(4)D
(5)A
(6)C
(7)D
(8)C
2.(1)60°
(2)22°
3.(1)∠DBC
两直线平行,同旁内角互补
∠DBC
等量代换
同旁内角互补,两直线平行
(2)AC
DE
同位角相等,两直线平行
∠C
两直线平行,同位角相等
90°
等量代换
BC
垂直定义
【拓展延伸训练】
1.因为∠A=∠D(已知),
所以AB∥CD(内错角相等,两直线平行),
所以∠C=∠B(两直线平行,内错角相等)
2.因为AB∥CD,AD∥BC(已知),
所以∠A+∠ADC=180°,∠A+∠ABC=180°(两直线平行,同旁内角互补).
所以∠ADC=∠ABC(同角的补角相等).
又因为∠EDF=∠ADC,∠EBF=∠ABC(已知),
所以∠EDF=∠EBF(等量代换),
又因为DC∥AB(已知),
所以∠DFB+∠FBE=180°(两直线平行,同旁内角互补),
所以∠DFB+∠EDF=180°(等量代换),
所以DE∥FB(同旁内角互补,两直线平行).
【自主探究提高】65°
平行线的性质
一、基础能力平台
1.选择题:
(1)下列说法中,不正确的是(
)
A.同位角相等,两直线平行;
B.两直线平行,内错角相等;
C.两直线被第三条直线所截,同旁内角互补;
D.同旁内角互补,两直线平行
(2)如图1所示,AC平分∠BCD,且∠BCA=∠CAD=∠CAB,∠ABC=75°,
则∠BCA等于(
)
A.36°
B.35°
C.
37.5°
D.70°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1)
(2)
(3)
(3)如图2所示,AD⊥BC于D,DG∥AB,那么∠B和∠ADG的关系是(
)
A.互余
B.互补
C.相等
D.以上都不对
(4)如图3,直线c与直线a、b相交,且a∥b,则下列结论:
①∠1=∠2;②∠1=∠3;③∠3=∠2中,正确的个数为(
)
A.0个
B.1个
C.2个
D.3个
(5)如图4,若AB∥CD,则(
)
A.∠1=∠2+∠3
B.∠1=∠3-∠2
C.∠1+∠2+∠3=180°
D.∠1-∠2+∠3=180°
(6)如图5,AB∥CD,AC⊥BC,图中与∠CAB互余的角有(
)
A.1个
B.2个
C.3个
D.4个
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(4)
(5)
(6)
(7)已知两个角的两边分别平行,并且这两个角的差是90°,则这两个角分别等于(
)
A.60°,150°
B.20°,110°
C.30°,120°
D.45°,135°
(8)如图6所示,若AB∥EF,用含α、β、γ的式子表示x,应为(
)
A.α+β+γ
B.β+γ-α
C.180°-α-γ+β
D.180°+α+β-γ
2.填空题:
(1)如图7,两平面镜α、β的夹角为θ,入射光线AO平行于β入射到α上,经两次反射后的出射光线O′B平行于α,则角θ=________.
(2)如图8所示,直线a∥b,则∠A=_______.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(7)
(8)
(9)
3.填写理由:
(1)如图9所示,因为DF∥AC(已知),
所以∠D+______=180°(__________________________)
因为∠C=∠D(已知),
所以∠C+_______=180°(_________________________)
所以DB∥EC(_________).
(2)如图所示,因为∠A=∠BDE(已知),
所以______∥_____(__________________________)
所以∠DEB=_______(_________________________)
因为∠C=90°(已知),
所以∠DEB=______(_________________________)
所以DE⊥______(_________________________)
二、拓展延伸训练
1.如图所示,已知AD、BC相交于O,∠A=∠D,试说明一定有∠C=∠B.
( http: / / www.21cnjy.com )
2.如图所示,已知AB∥CD,AD∥BC,BF平分∠ABC,DE平分∠ADC,则一定有DE∥FB,它的根据是什么?
( http: / / www.21cnjy.com )
三、自主探究提高
如图,AB∥CD,EF分别交AB、CD于M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
( http: / / www.21cnjy.com )
答案:
【基础能力平台】
1.(1)C
(2)B
(3)A
(4)D
(5)A
(6)C
(7)D
(8)C
2.(1)60°
(2)22°
3.(1)∠DBC
两直线平行,同旁内角互补
∠DBC
等量代换
同旁内角互补,两直线平行
(2)AC
DE
同位角相等,两直线平行
∠C
两直线平行,同位角相等
90°
等量代换
BC
垂直定义
【拓展延伸训练】
1.因为∠A=∠D(已知),
所以AB∥CD(内错角相等,两直线平行),
所以∠C=∠B(两直线平行,内错角相等)
2.因为AB∥CD,AD∥BC(已知),
所以∠A+∠ADC=180°,∠A+∠ABC=180°(两直线平行,同旁内角互补).
所以∠ADC=∠ABC(同角的补角相等).
又因为∠EDF=∠ADC,∠EBF=∠ABC(已知),
所以∠EDF=∠EBF(等量代换),
又因为DC∥AB(已知),
所以∠DFB+∠FBE=180°(两直线平行,同旁内角互补),
所以∠DFB+∠EDF=180°(等量代换),
所以DE∥FB(同旁内角互补,两直线平行).
【自主探究提高】65°
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
