浙教版七年级下册1.2 同位角、内错角、同旁内角 课件(共17张PPT)
文档属性
| 名称 | 浙教版七年级下册1.2 同位角、内错角、同旁内角 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 22:26:37 | ||
图片预览

文档简介
(共17张PPT)
1.2 同位角、内错角、同旁内角
浙教新版七年级《数学》下册
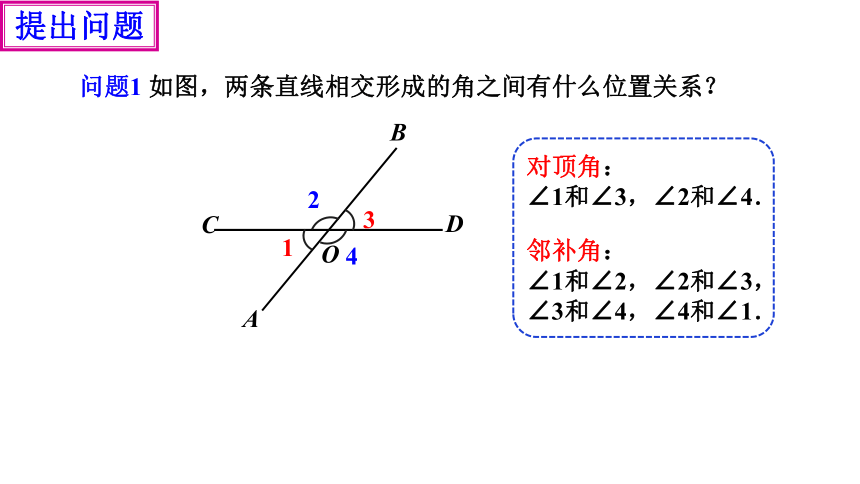
问题1 如图,两条直线相交形成的角之间有什么位置关系?
O
B
A
D
C
1
2
3
4
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
提出问题
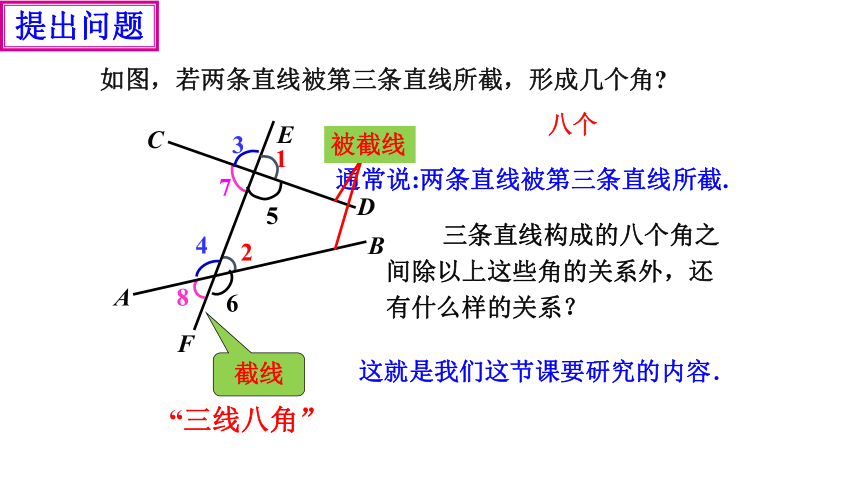
如图,若两条直线被第三条直线所截,形成几个角
1
3
7
5
2
4
8
6
D
C
A
B
E
F
三条直线构成的八个角之间除以上这些角的关系外,还有什么样的关系?
这就是我们这节课要研究的内容.
“三线八角”
八个
通常说:两条直线被第三条直线所截.
截线
被截线
提出问题
F
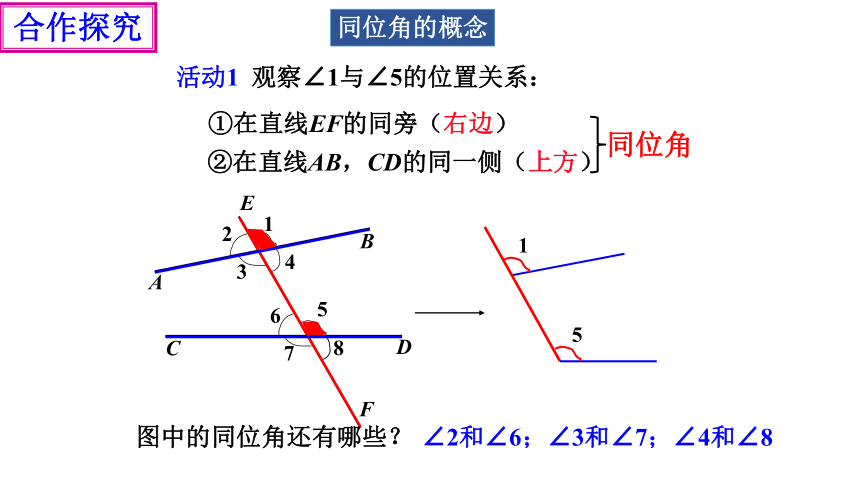
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB,CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
同位角的概念
合作探究
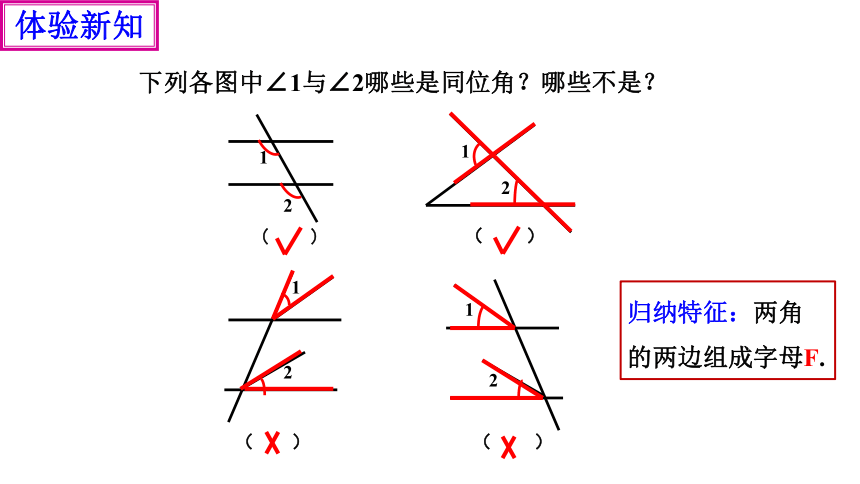
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
归纳特征:两角的两边组成字母F.
体验新知
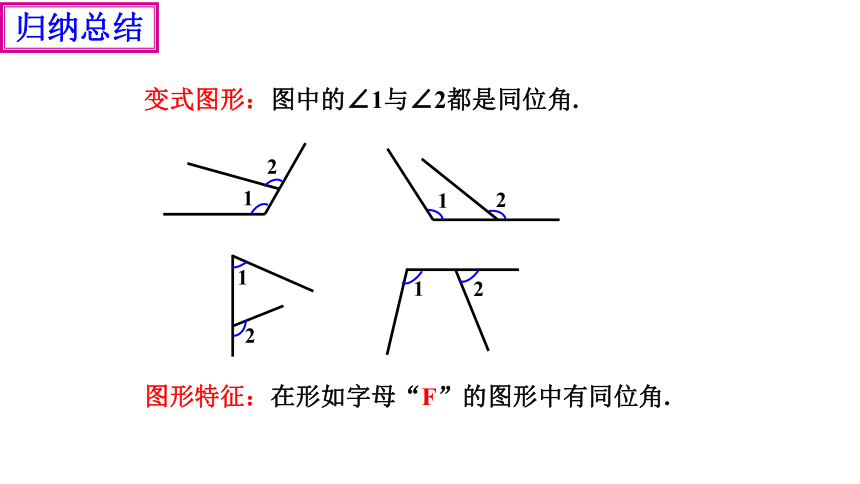
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
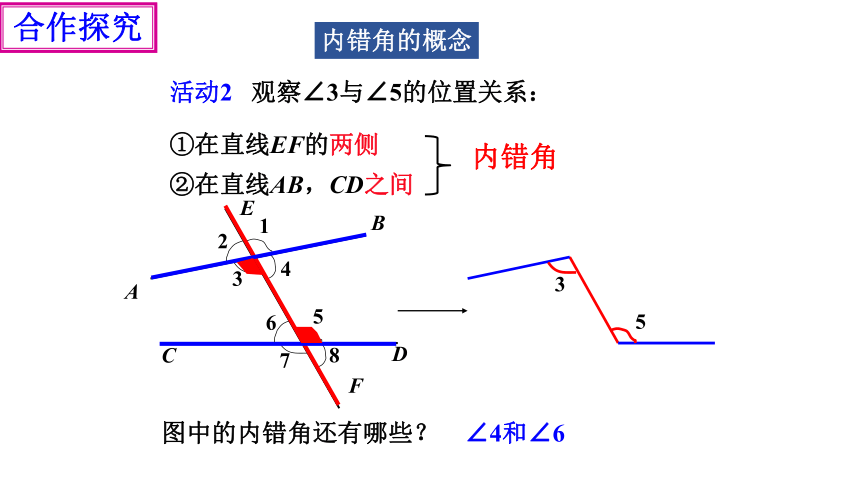
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB,CD之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
内错角的概念
合作探究
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB,CD之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
同旁内角的概念
合作探究
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
在三线八角中
①同位角有:
②内错角有:
③同旁内角有:
∠1和∠2
∠3和∠4
∠5和∠6
∠7和∠8
∠7和∠2
∠5和∠4
∠7和∠4
∠5和∠2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
归纳总结
1.识别哪些角是同位角、内错角、同旁内角.
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
体验新知
2.(1)∠1和∠4是直线_____与直线____被直线______所截
形成的________.
(2)∠2和∠3是直线_____与直线_____被直线_______所截
形成的________.
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
2
3
1
4
(1)
(2)
体验新知
3.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角
可看成是( )
A.对顶角 B.同位角
C.内错角 D.同旁内角
C
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
体验新知
例 如图所示,直线DE 交∠ABC 的边BA于点F .如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补.请说明理由
解:∵∠2与∠4是对顶角,
∴∠2=∠4.
又∵∠1=∠2,
∴∠1=∠4(等量代换).
∵∠2与∠3互为补角,
∴∠2+∠3=180°,
∴∠1+∠3=180°,
即∠1与∠3互补.
例题精讲
对顶角
同位角 同旁内角 内错角
角与角的关系
课堂练习
完成教材第14页,课内练习:2;
教材第15页,作业题:2、5
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同 位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称)也是符合的.
小结提升
1.2 同位角、内错角、同旁内角
浙教新版七年级《数学》下册
问题1 如图,两条直线相交形成的角之间有什么位置关系?
O
B
A
D
C
1
2
3
4
对顶角:
∠1和∠3,∠2和∠4.
邻补角:
∠1和∠2,∠2和∠3,
∠3和∠4,∠4和∠1.
提出问题
如图,若两条直线被第三条直线所截,形成几个角
1
3
7
5
2
4
8
6
D
C
A
B
E
F
三条直线构成的八个角之间除以上这些角的关系外,还有什么样的关系?
这就是我们这节课要研究的内容.
“三线八角”
八个
通常说:两条直线被第三条直线所截.
截线
被截线
提出问题
F
活动1 观察∠1与∠5的位置关系:
①在直线EF的同旁(右边)
②在直线AB,CD的同一侧(上方)
A
C
B
D
E
1
2
3
4
5
6
7
8
1
5
∠2和∠6;∠3和∠7;∠4和∠8
图中的同位角还有哪些?
同位角
同位角的概念
合作探究
下列各图中∠1与∠2哪些是同位角?哪些不是?
1
2
( )
1
2
( )
( )
1
2
( )
1
2
归纳特征:两角的两边组成字母F.
体验新知
图形特征:在形如字母“F”的图形中有同位角.
变式图形:图中的∠1与∠2都是同位角.
1
2
1
2
1
2
1
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动2 观察∠3与∠5的位置关系:
①在直线EF的两侧
②在直线AB,CD之间
3
5
∠4和∠6
图中的内错角还有哪些?
内错角
内错角的概念
合作探究
变式图形:图中的∠1与∠2都是内错角.
图形特征:在形如“Z”的图形中有内错角.
1
2
1
1
1
2
2
2
归纳总结
A
C
B
D
E
F
1
2
3
4
5
6
7
8
活动3 观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB,CD之间
4
5
∠3和∠6
图中还有哪些同旁内角?
同旁内角
同旁内角的概念
合作探究
变式图形:图中的∠1与∠2都是同旁内角.
图形特征:在形如“U”的图形中有同旁内角.
1
1
1
1
2
2
2
2
归纳总结
在三线八角中
①同位角有:
②内错角有:
③同旁内角有:
∠1和∠2
∠3和∠4
∠5和∠6
∠7和∠8
∠7和∠2
∠5和∠4
∠7和∠4
∠5和∠2
F
1
3
7
5
2
4
8
6
D
C
A
B
E
归纳总结
1.识别哪些角是同位角、内错角、同旁内角.
1
2
(1)
同位角
1
2
(2)
1
2
(3)
1
2
(4)
1
2
(5)
a
b
c
1
2
(6)
1
2
(7)
1
2
(8)
1
2
1
2
(9)
(10)
同位角
同位角
同位角
同位角
内错角
同旁内角
体验新知
2.(1)∠1和∠4是直线_____与直线____被直线______所截
形成的________.
(2)∠2和∠3是直线_____与直线_____被直线_______所截
形成的________.
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
2
3
1
4
(1)
(2)
体验新知
3.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角
可看成是( )
A.对顶角 B.同位角
C.内错角 D.同旁内角
C
生活中的数学:三线八角手势记忆法
同位角
内错角
同旁内角
体验新知
例 如图所示,直线DE 交∠ABC 的边BA于点F .如果内错角∠1与∠2相等,那么同位角∠1与∠4相等,同旁内角∠1与∠3互补.请说明理由
解:∵∠2与∠4是对顶角,
∴∠2=∠4.
又∵∠1=∠2,
∴∠1=∠4(等量代换).
∵∠2与∠3互为补角,
∴∠2+∠3=180°,
∴∠1+∠3=180°,
即∠1与∠3互补.
例题精讲
对顶角
同位角 同旁内角 内错角
角与角的关系
课堂练习
完成教材第14页,课内练习:2;
教材第15页,作业题:2、5
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型
同旁内角 “U”型
2. 在图形中判断三线八角的方法(描图法):
①把两个角在图中描画出来;
②找到两个角的公共直线;
③观察所描的角,判断所属“字母”类型,同 位角为“F”型,内错角为“Z”型,同旁内角为“U”型,注意图形的变式(旋转、对称)也是符合的.
小结提升
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
