浙教版七年级下册1.4 平行线的性质 课件(共26张PPT)
文档属性
| 名称 | 浙教版七年级下册1.4 平行线的性质 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
1.4.1平行线的性质
5、在同一平面内,垂直于同一条直线的两条直线互相平行;
6、平行于同一条直线的两条直线互相平行.
判定平行线的方法:
1、平行线的定义:在同一平面内不相交的两条直线.
2、同位角相等,两直线平行;
3、内错角相等,两直线平行;
4、同旁内角互补,两直线平行;
a
b
c
c
a
b
导入新课
导入新课
问题1:判定两条直线平行,我们学过的有哪几种最常用方法?
方法1:同位角相等,两直线平行.
方法2:内错角相等,两直线平行.
方法3:同旁内角互补,两直线平行.
如果反过来,两直线平行,同位角、内错角、同旁内角又有怎样的关系呢?
实 验
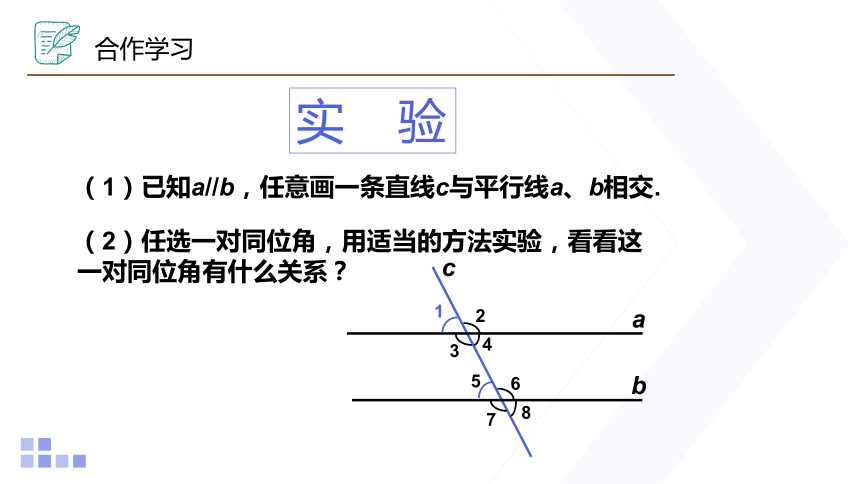
(1)已知a//b,任意画一条直线c与平行线a、b相交.
c
a
b
1
5
2
3
4
6
7
8
(2)任选一对同位角,用适当的方法实验,看看这一对同位角有什么关系?
合作学习
65°
65°
c
a
b
1
5
2
3
4
6
7
8
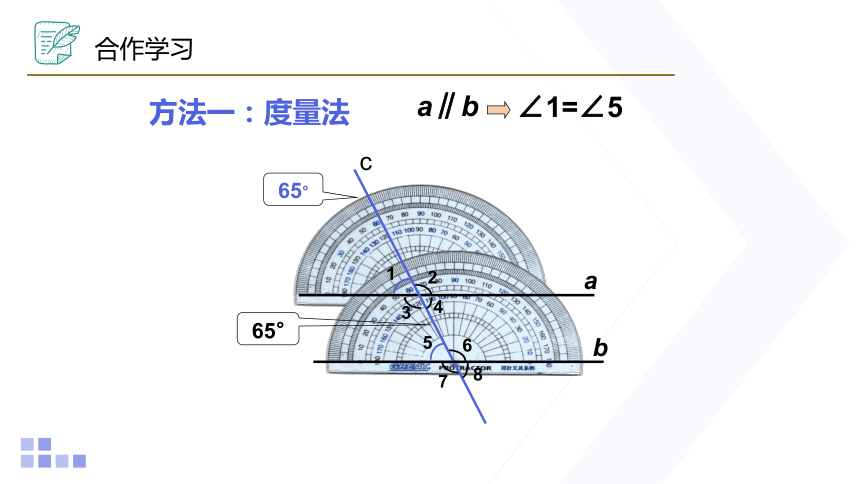
∠1=∠5
a∥b
方法一:度量法
合作学习
1
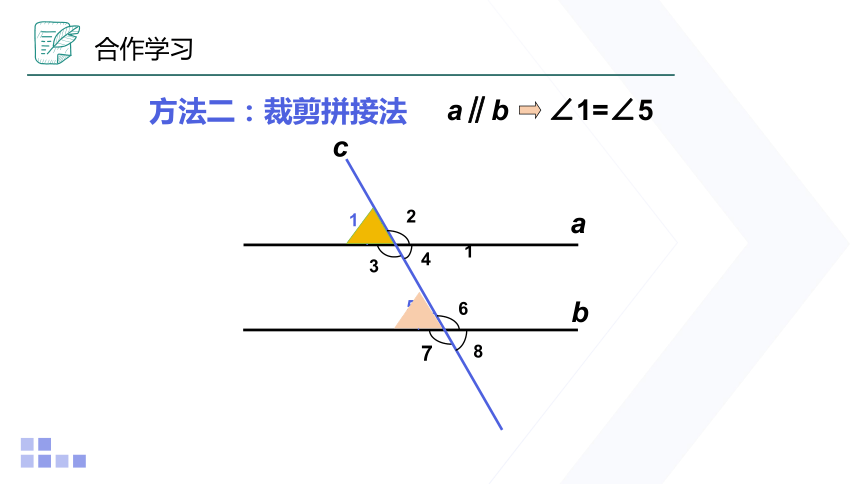
方法二:裁剪拼接法
b
5
6
8
a
c
2
3
4
7
1
∠1=∠5
a∥b
合作学习
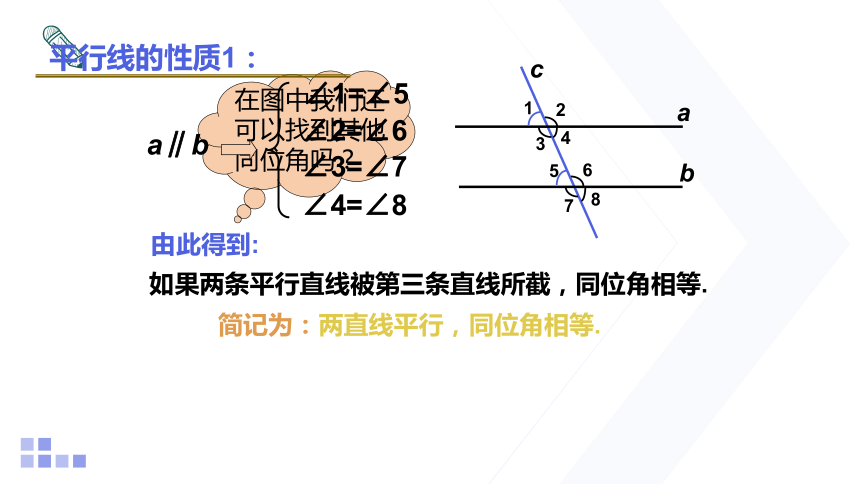
在图中我们还可以找到其他同位角吗?
简记为:两直线平行,同位角相等.
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
如果两条平行直线被第三条直线所截,同位角相等.
由此得到:
c
a
b
1
5
2
3
4
6
7
8
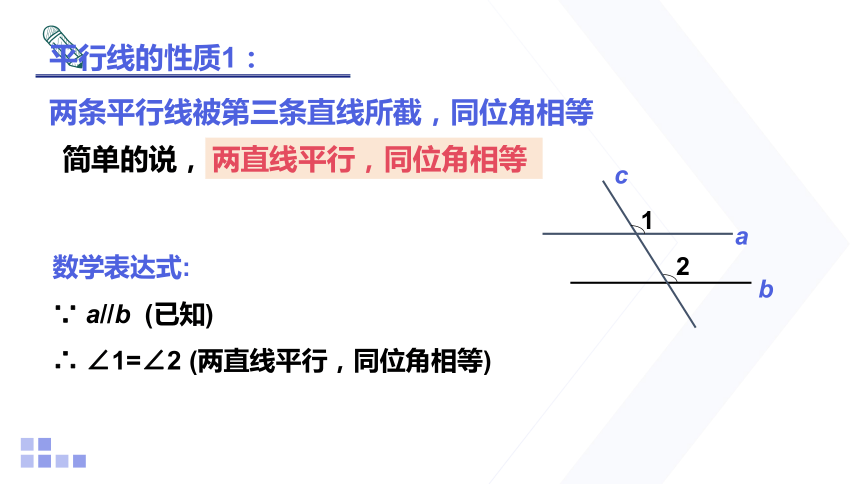
平行线的性质1:
两条平行线被第三条直线所截,同位角相等
两直线平行,同位角相等
数学表达式:
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
c
a
b
1
2
简单的说,
平行线的性质1:
c
a
b
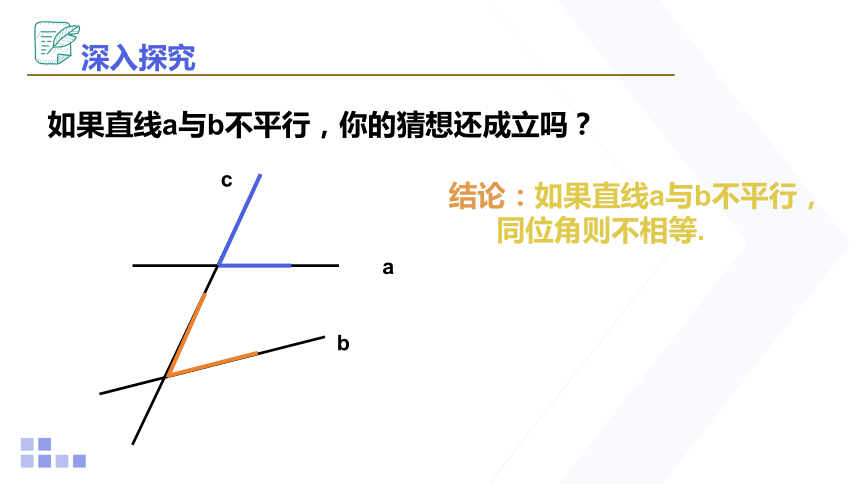
如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行,
同位角则不相等.
深入探究
判定定理
同位角相等
平行线判定定理和性质定理有什么区别?
发现:二者条件与结论正好相反
性质定理
条件
结论
条件
结论
两直线平行
同位角相等
两直线平行
新课讲解
1.如图 AB∥CD,∠α=45°,∠D=∠C
那么∠ D= ,
∠C= ,
∠ B= 。
A
B
C
D
α
45°
45°
45°
135°
针对训练
3.如图,已知直线l1, l2, l3, l4 . 若∠1= ∠ 2,则∠3= ∠4. 完成下面的说理过程(填空)
解:已知∠1= ∠ 2,
根据(________________________)
得______//______.
再根据(_________________________)
得∠3= ∠4.
内错角相等,两直线平行
两直线平行,同位角相等
l2
l1
l3
l1
l2
3
1
2
4
P15,课内练习2
例1:如图, 梯子的各条横档互相平行, ∠1=100°,求∠2的度数。
经典例题
解
∵AB∥CD(已知)
∴∠3=∠1=100o
∴∠2=1800-∠3=80o
(平行线的性质)
(平角的意义)
1
2
A
B
C
D
3
例2: 如图:已知∠1=∠2.若直线b⊥m,则直线a⊥m,请说明理由.
经典例题
解 ∵ ∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
∴ ∠3=∠4
( 两直线平行,同位角相等)
∵b⊥m(已知)
∴ ∠4=900( )
垂直的意义
∴ ∠3=900
∴a⊥m
1
2
3
4
n
m
a
b
1
2
1.如图:已知直线l1∥l2,∠1=40o,求∠2的度数.
P15 课内练习1
2.如图,已知直线l1 ,l2 ,l3 ,l4.∠1=∠2,则 ∠3=∠4.完成下面的说理过程(填空).
解:已知∠1=∠2,
根据(______________________),
得____∥____.
再根据(______________________),
得∠3=∠4.
内错角相等,两直线平行
1
2
3
4
两直线平行,同位角相等
l1
l2
P15 课内练习2
3.如图,已知a,b,c,d四条直线.
(1)图中哪些直线互相平行?哪些直线相交?
(2)说出∠a的度数.
76°
76°
77°
P16 课内练习3
2.如图AB∥CD,∠E=40°,∠A=110°,求∠C的度数.
解:∵AB∥CD,∴∠A+∠AFD=180°,
∵∠A=110°∴∠AFD=70°∴∠CFE=∠AFD=70°
∵∠E=40°,
∴∠C=180°﹣∠E﹣∠CFE=180°﹣40°﹣70°=70°
针对练习
B
1、如图,直线a∥b,若∠2=55°,∠3=100°,
则∠1的度数为( )
A.35° B.45° C.50° D.55°
基础巩固
2、如图,AB∥CD,∠B=68°,∠E=20°,
则∠D的度数为( )
A.28° B.38° C.48° D.88°
C
基础巩固
3.如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)∠1与∠2有什么数量关系,为什么?
(2)BE与DF有什么位置关系?请说明理由.
解:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
基础巩固
作业题4、5
PART 01
课堂小结
如果两条平行直线被第三条直线所截,同位角相等
c
a
b
1
5
2
3
4
6
7
8
数学表达式:
简单地说:
两直线平行,同位角相等.
∴ ∠1=∠5
∴ ∠2=∠6
∴ ∠3=∠7
∴ ∠4=∠8
根据“两直线平行,同位角相等”
∵ a//b (已知)
2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞。 爱拉斯托塞博学多才。
细心的爱拉斯托塞发现:离亚历山大城A约785公里的塞尼城S,夏日正午的阳光可以一直照到井底,也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小
木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50 .
E
D
B
1
S
A
O
2
C
2、第一个算出地球周长的人
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,即AD ∥SE,所以∠1= ∠2.
两直线平行,同位角相等。
那么∠2的度数也等于360°的1/50 ,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50 .而亚历山大城到塞尼城的距离约为785公里,785×50=369250公里,这是一个相当精确的结果.
地球周长测出来啦!
1.4.1平行线的性质
5、在同一平面内,垂直于同一条直线的两条直线互相平行;
6、平行于同一条直线的两条直线互相平行.
判定平行线的方法:
1、平行线的定义:在同一平面内不相交的两条直线.
2、同位角相等,两直线平行;
3、内错角相等,两直线平行;
4、同旁内角互补,两直线平行;
a
b
c
c
a
b
导入新课
导入新课
问题1:判定两条直线平行,我们学过的有哪几种最常用方法?
方法1:同位角相等,两直线平行.
方法2:内错角相等,两直线平行.
方法3:同旁内角互补,两直线平行.
如果反过来,两直线平行,同位角、内错角、同旁内角又有怎样的关系呢?
实 验
(1)已知a//b,任意画一条直线c与平行线a、b相交.
c
a
b
1
5
2
3
4
6
7
8
(2)任选一对同位角,用适当的方法实验,看看这一对同位角有什么关系?
合作学习
65°
65°
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
a∥b
方法一:度量法
合作学习
1
方法二:裁剪拼接法
b
5
6
8
a
c
2
3
4
7
1
∠1=∠5
a∥b
合作学习
在图中我们还可以找到其他同位角吗?
简记为:两直线平行,同位角相等.
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
如果两条平行直线被第三条直线所截,同位角相等.
由此得到:
c
a
b
1
5
2
3
4
6
7
8
平行线的性质1:
两条平行线被第三条直线所截,同位角相等
两直线平行,同位角相等
数学表达式:
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
c
a
b
1
2
简单的说,
平行线的性质1:
c
a
b
如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行,
同位角则不相等.
深入探究
判定定理
同位角相等
平行线判定定理和性质定理有什么区别?
发现:二者条件与结论正好相反
性质定理
条件
结论
条件
结论
两直线平行
同位角相等
两直线平行
新课讲解
1.如图 AB∥CD,∠α=45°,∠D=∠C
那么∠ D= ,
∠C= ,
∠ B= 。
A
B
C
D
α
45°
45°
45°
135°
针对训练
3.如图,已知直线l1, l2, l3, l4 . 若∠1= ∠ 2,则∠3= ∠4. 完成下面的说理过程(填空)
解:已知∠1= ∠ 2,
根据(________________________)
得______//______.
再根据(_________________________)
得∠3= ∠4.
内错角相等,两直线平行
两直线平行,同位角相等
l2
l1
l3
l1
l2
3
1
2
4
P15,课内练习2
例1:如图, 梯子的各条横档互相平行, ∠1=100°,求∠2的度数。
经典例题
解
∵AB∥CD(已知)
∴∠3=∠1=100o
∴∠2=1800-∠3=80o
(平行线的性质)
(平角的意义)
1
2
A
B
C
D
3
例2: 如图:已知∠1=∠2.若直线b⊥m,则直线a⊥m,请说明理由.
经典例题
解 ∵ ∠1=∠2(已知)
∴a∥b(同位角相等,两直线平行)
∴ ∠3=∠4
( 两直线平行,同位角相等)
∵b⊥m(已知)
∴ ∠4=900( )
垂直的意义
∴ ∠3=900
∴a⊥m
1
2
3
4
n
m
a
b
1
2
1.如图:已知直线l1∥l2,∠1=40o,求∠2的度数.
P15 课内练习1
2.如图,已知直线l1 ,l2 ,l3 ,l4.∠1=∠2,则 ∠3=∠4.完成下面的说理过程(填空).
解:已知∠1=∠2,
根据(______________________),
得____∥____.
再根据(______________________),
得∠3=∠4.
内错角相等,两直线平行
1
2
3
4
两直线平行,同位角相等
l1
l2
P15 课内练习2
3.如图,已知a,b,c,d四条直线.
(1)图中哪些直线互相平行?哪些直线相交?
(2)说出∠a的度数.
76°
76°
77°
P16 课内练习3
2.如图AB∥CD,∠E=40°,∠A=110°,求∠C的度数.
解:∵AB∥CD,∴∠A+∠AFD=180°,
∵∠A=110°∴∠AFD=70°∴∠CFE=∠AFD=70°
∵∠E=40°,
∴∠C=180°﹣∠E﹣∠CFE=180°﹣40°﹣70°=70°
针对练习
B
1、如图,直线a∥b,若∠2=55°,∠3=100°,
则∠1的度数为( )
A.35° B.45° C.50° D.55°
基础巩固
2、如图,AB∥CD,∠B=68°,∠E=20°,
则∠D的度数为( )
A.28° B.38° C.48° D.88°
C
基础巩固
3.如图,四边形ABCD中,∠A=∠C=90°,BE,DF分别是∠ABC,∠ADC的平分线.
(1)∠1与∠2有什么数量关系,为什么?
(2)BE与DF有什么位置关系?请说明理由.
解:(1)∠1+∠2=90°;
∵BE,DF分别是∠ABC,∠ADC的平分线,
∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∴2(∠1+∠2)=180°
∴∠1+∠2=90°;
(2)BE∥DF;
在△FCD中,∵∠C=90°,
∴∠DFC+∠2=90°,
∵∠1+∠2=90°,
∴∠1=∠DFC,
∴BE∥DF.
基础巩固
作业题4、5
PART 01
课堂小结
如果两条平行直线被第三条直线所截,同位角相等
c
a
b
1
5
2
3
4
6
7
8
数学表达式:
简单地说:
两直线平行,同位角相等.
∴ ∠1=∠5
∴ ∠2=∠6
∴ ∠3=∠7
∴ ∠4=∠8
根据“两直线平行,同位角相等”
∵ a//b (已知)
2000多年前,有人用简单的测量工具计算出地球的周长。这个人就是古希腊的爱拉斯托塞。 爱拉斯托塞博学多才。
细心的爱拉斯托塞发现:离亚历山大城A约785公里的塞尼城S,夏日正午的阳光可以一直照到井底,也就是说,在那一时刻,太阳正好悬挂在塞尼城的正上方E,阳光能够只指地心O.而在此时他所在的亚历山大城阳光却不能直接射到水井的底部.爱拉斯托塞在地上竖起一根小
木棍AC,测量天顶方向AB与太阳方向AD之间的夹角∠1,发现这个夹角等于360°的1/50 .
E
D
B
1
S
A
O
2
C
2、第一个算出地球周长的人
E
D
B
1
S
A
O
2
C
由于太阳离地球非常遥远,把射到地球上的阳光看作是彼此平行的,即AD ∥SE,所以∠1= ∠2.
两直线平行,同位角相等。
那么∠2的度数也等于360°的1/50 ,所以,亚历山大城到塞尼城的距离弧AS也等于整个地球周长的1/50 .而亚历山大城到塞尼城的距离约为785公里,785×50=369250公里,这是一个相当精确的结果.
地球周长测出来啦!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
