七年级下数学第一章 认识三角形的知识点汇总
文档属性
| 名称 | 七年级下数学第一章 认识三角形的知识点汇总 |

|
|
| 格式 | rar | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-07 00:00:00 | ||
图片预览

文档简介
课程标准浙江版教材 七年级(下)数学
第一章
第一节 认识三角形
一、三角形基本概念
1、三角形定义:由不在同一直线上的三条线段首尾顺次连结所组成的图形,叫做三角形。
三角形的表示 记作△ABC
三角形的边 AB、BC、CA
三角形的顶点 A B C
三角形的内角 ∠A、∠B、∠C
二、三角形基本知识点
三角形三边的关系
三角形任意两边之和大于第三边。
三角形任意两边之差小于第三边。
练习
1、已知线段a=7cm,b=4cm, =3cm,这三条线段能否组成三角形,为什么?
2、三条线段的长度分别为:
(1)3、8、10 (2)5、2、7
(3)5、5、11 (4)13、12、20
能组成三角形的有( )组。
A、1 B、2 C、3 D、4
3、在△ABC中,AB=7 BC=3,
并且AC为奇数,那么△ABC的周长为多少。
2、三角形的三个内角有什么关系?
三角形三个内角的和等于180 。
练习 1、如图 ,在△ABC中,∠A=45°, ∠B=30°, 求∠C的度数。
直角三角形的两个锐角互余。
三角形的外角:
由三角形一条边的延长线和另一条相邻的边组成的角,叫做该三角形的外角.
三角形外角性质:
1、三角形的一个外角等于和它不相邻的两个内角的和
2、三角形的一个外角等于和它不相邻的两个内角的和。
3、三角形的一个外角大于任何一个和它不相邻的内角。
思考:三角形的三个外角的度数的和是多少度?
练习
一把椅子的结构如图,∠1=∠2。当椅面水平时,
∠3=100°,此时∠1的度数是多少?
三、本节小结
1、由三条线段___所组成图形叫做三角形。
2、组成三角形的___叫做三角形的边,相邻两边的公共端点叫做三角形的___。三角形__组成的角叫做三角形的内角,简称三角形的角。
3、三角形任何两边的__大于第三边。三角形任何两边的__小于第三边。
3、判断三条已知线段能否组成三角形,需要把每一条线段与其余两条线段的和比较大小。如果____,那么这三条线段就组成一个三角形,否则不能组成三角形。这可归结为把_____的一条线段和另两条线段的和作比较。
4、三角形的一边与另一边的反向延长线组成的角叫做____
5、三角形按角分类:
在三角形的三个角中找出一个角是直角或是钝角,就能判定它是直角三角形或者是钝角三角形,但如可判定它是锐角三角形,就必须知道三个角都是锐角才行。
3、三角形的内角和等于180°。
4、三角形的一个外角等于不相邻的两个内角的和;
大于任何一个不相邻的内角。
四、本节综合练习
如图,在△ABC中,∠C是直角,D是BC上的一点。已知∠1= ∠2, ∠B=25°,求∠BAD
的度数。
三角形的角平分线和中线
一、基本概念
1、三角形角平分线的概念:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
如图,
∠BAC的平分线交BC于点D,线段AD就是
ΔABC的一条角平分线。
三角形的三条角平分线会交于同一点。
三角形的中线
三角形中线的定义:在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。
任意画一个⊿ABC,用刻度尺画BC的中点D,连结AD。
如图,D为BC的中点,AD是⊿ABC中BC边上的中线。
三角形的三条中线会交于同一点,称为三角形的重心。
三角形的一条中线把三角形分成两个面积相等的小三角形。
练习
1、如图,AF是ΔABC的角平分线,AE是BC边上的中线,选择“>”“<”或“=”号填空:
(1)BE___EC
(2)∠CAF___―∠BAC
(3)∠AFB___∠C+∠FAB
(4)∠AEC___∠B
2、如图,在ΔABC中,∠ACB=90°,CE是ΔABC的角平分线,已知∠CEB=110°,求∠A和∠B的度数。
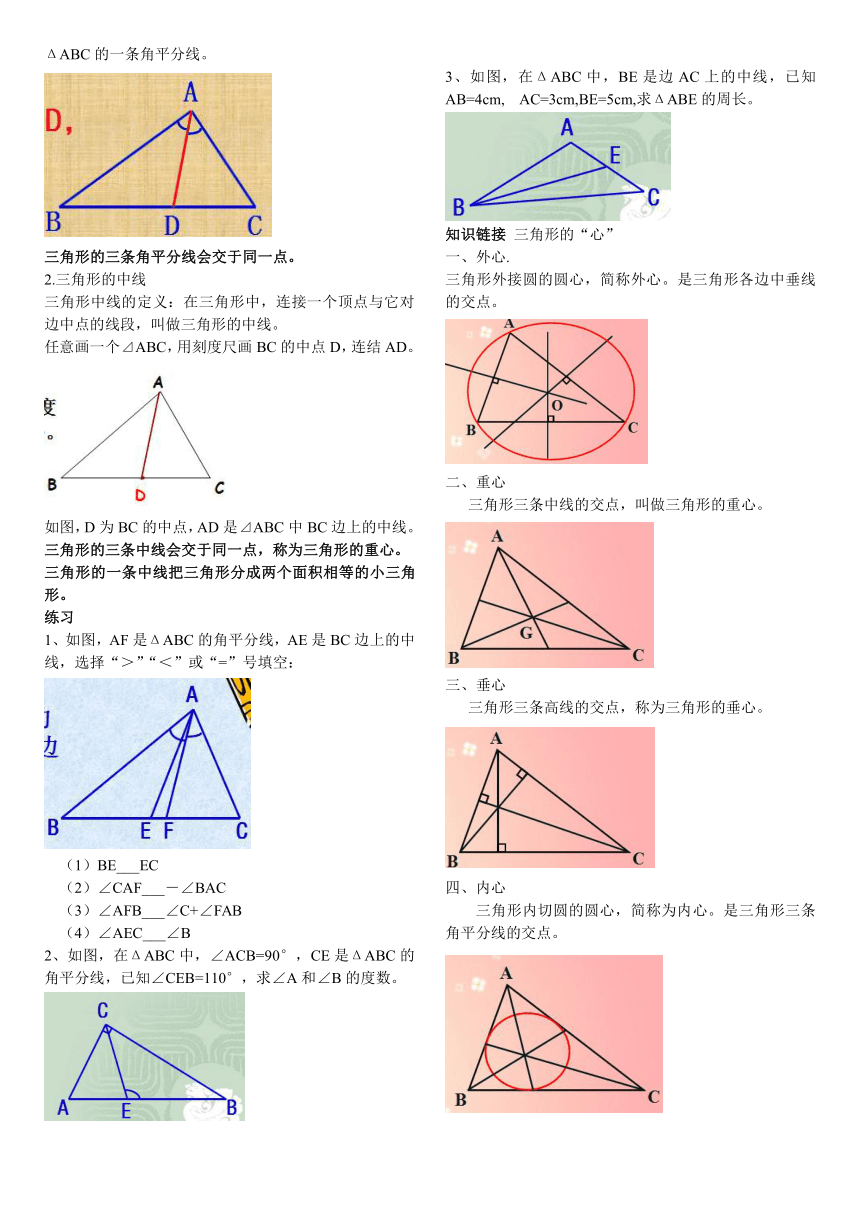
3、如图,在ΔABC中,BE是边AC上的中线,已知AB=4cm, AC=3cm,BE=5cm,求ΔABE的周长。
知识链接 三角形的“心”
一、外心.
三角形外接圆的圆心,简称外心。是三角形各边中垂线的交点。
二、重心
三角形三条中线的交点,叫做三角形的重心。
三、垂心
三角形三条高线的交点,称为三角形的垂心。
四、内心
三角形内切圆的圆心,简称为内心。是三角形三条角平分线的交点。
三角形的高
三角形的高的定义: 从三角形中一个顶点向它对边所在直线做垂线,顶点和垂足之间的线段,叫做三角形的高.
∵AD是△ ABC中BC的 高
∴AD ⊥BC
练习
1、如图1-15,在△ABC中,AE,AD分别是BC边上中线和高,说明△ABE的面积与△AEC的面积相等.
结论:
同高等底的两个三角形的面积相等。
三角形额中线把三角形分成两个面积相等的三角形
2、如图1-16,点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少
(2)由第(1)题,你能求出△DEC的面积吗 △AEF和△FBD的面积呢
全等三角形
知识结构
两个三角形全等的判断方法
1、边边边(SSS) :三条边对应相等的两个三角 形全等。
2、边角边(SAS):有两边及其夹角对应相等的两个三角形全等。
3、角边角 (ASA) :有两角及其夹边对应相等的两个三角形全等。
4、角角边(AAS):有两角及一角的对边对应相 等的两个三角形全等。
三、线段中垂线与角平分线的性质
1、 线段垂直平分线的性质:
线段的垂直平分线上的点到线段两端点的距离相等。
几何表述:
∵ 是线段AB的中垂线,点C在L上
∴ CA=CB
2、角平分线的性质:
角平分线上点到角两边距离相等
几何表述:
∵点P是∠BAC的平分线上的一点且PB⊥AB,PC ⊥AC,
∴PB=PC的理由
三、全等概念
记作:“ ABC≌ DEF”
互相重合的顶点叫对应顶点,如A与D
请指出其他的对应顶点:
互相重合的边叫对应边,AB边与DE
请指出其他的对应边:
3、互相重合的角叫对应角,如
请指出其他的对应角:
练习:
、如图,△ABC中,DE垂直平分AC,AE=3cm, △ABC的周长是9cm,则△ABC的周长是_______.
如图,BE、CF是△ABC 的角平分线,∠A=40°。则∠BOC=( )度
3、下列说法正确的是( )
A、有一个外角是钝角的三角形必定是锐角三角形
B、三条线段a,b,c,若满足a>b>c,且aC、有两个角和一条边彼此相等的两个三角形全等
D、有两条边和一个角对应相等的两个三角形全等
第一章
第一节 认识三角形
一、三角形基本概念
1、三角形定义:由不在同一直线上的三条线段首尾顺次连结所组成的图形,叫做三角形。
三角形的表示 记作△ABC
三角形的边 AB、BC、CA
三角形的顶点 A B C
三角形的内角 ∠A、∠B、∠C
二、三角形基本知识点
三角形三边的关系
三角形任意两边之和大于第三边。
三角形任意两边之差小于第三边。
练习
1、已知线段a=7cm,b=4cm, =3cm,这三条线段能否组成三角形,为什么?
2、三条线段的长度分别为:
(1)3、8、10 (2)5、2、7
(3)5、5、11 (4)13、12、20
能组成三角形的有( )组。
A、1 B、2 C、3 D、4
3、在△ABC中,AB=7 BC=3,
并且AC为奇数,那么△ABC的周长为多少。
2、三角形的三个内角有什么关系?
三角形三个内角的和等于180 。
练习 1、如图 ,在△ABC中,∠A=45°, ∠B=30°, 求∠C的度数。
直角三角形的两个锐角互余。
三角形的外角:
由三角形一条边的延长线和另一条相邻的边组成的角,叫做该三角形的外角.
三角形外角性质:
1、三角形的一个外角等于和它不相邻的两个内角的和
2、三角形的一个外角等于和它不相邻的两个内角的和。
3、三角形的一个外角大于任何一个和它不相邻的内角。
思考:三角形的三个外角的度数的和是多少度?
练习
一把椅子的结构如图,∠1=∠2。当椅面水平时,
∠3=100°,此时∠1的度数是多少?
三、本节小结
1、由三条线段___所组成图形叫做三角形。
2、组成三角形的___叫做三角形的边,相邻两边的公共端点叫做三角形的___。三角形__组成的角叫做三角形的内角,简称三角形的角。
3、三角形任何两边的__大于第三边。三角形任何两边的__小于第三边。
3、判断三条已知线段能否组成三角形,需要把每一条线段与其余两条线段的和比较大小。如果____,那么这三条线段就组成一个三角形,否则不能组成三角形。这可归结为把_____的一条线段和另两条线段的和作比较。
4、三角形的一边与另一边的反向延长线组成的角叫做____
5、三角形按角分类:
在三角形的三个角中找出一个角是直角或是钝角,就能判定它是直角三角形或者是钝角三角形,但如可判定它是锐角三角形,就必须知道三个角都是锐角才行。
3、三角形的内角和等于180°。
4、三角形的一个外角等于不相邻的两个内角的和;
大于任何一个不相邻的内角。
四、本节综合练习
如图,在△ABC中,∠C是直角,D是BC上的一点。已知∠1= ∠2, ∠B=25°,求∠BAD
的度数。
三角形的角平分线和中线
一、基本概念
1、三角形角平分线的概念:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
如图,
∠BAC的平分线交BC于点D,线段AD就是
ΔABC的一条角平分线。
三角形的三条角平分线会交于同一点。
三角形的中线
三角形中线的定义:在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。
任意画一个⊿ABC,用刻度尺画BC的中点D,连结AD。
如图,D为BC的中点,AD是⊿ABC中BC边上的中线。
三角形的三条中线会交于同一点,称为三角形的重心。
三角形的一条中线把三角形分成两个面积相等的小三角形。
练习
1、如图,AF是ΔABC的角平分线,AE是BC边上的中线,选择“>”“<”或“=”号填空:
(1)BE___EC
(2)∠CAF___―∠BAC
(3)∠AFB___∠C+∠FAB
(4)∠AEC___∠B
2、如图,在ΔABC中,∠ACB=90°,CE是ΔABC的角平分线,已知∠CEB=110°,求∠A和∠B的度数。
3、如图,在ΔABC中,BE是边AC上的中线,已知AB=4cm, AC=3cm,BE=5cm,求ΔABE的周长。
知识链接 三角形的“心”
一、外心.
三角形外接圆的圆心,简称外心。是三角形各边中垂线的交点。
二、重心
三角形三条中线的交点,叫做三角形的重心。
三、垂心
三角形三条高线的交点,称为三角形的垂心。
四、内心
三角形内切圆的圆心,简称为内心。是三角形三条角平分线的交点。
三角形的高
三角形的高的定义: 从三角形中一个顶点向它对边所在直线做垂线,顶点和垂足之间的线段,叫做三角形的高.
∵AD是△ ABC中BC的 高
∴AD ⊥BC
练习
1、如图1-15,在△ABC中,AE,AD分别是BC边上中线和高,说明△ABE的面积与△AEC的面积相等.
结论:
同高等底的两个三角形的面积相等。
三角形额中线把三角形分成两个面积相等的三角形
2、如图1-16,点D,E,F 分别是△ABC的三条边的中点.设△ABC的面积为S,求△DEF的面积.
你可以这样考虑:
(1)连结AD. △ADC的面积是多少
(2)由第(1)题,你能求出△DEC的面积吗 △AEF和△FBD的面积呢
全等三角形
知识结构
两个三角形全等的判断方法
1、边边边(SSS) :三条边对应相等的两个三角 形全等。
2、边角边(SAS):有两边及其夹角对应相等的两个三角形全等。
3、角边角 (ASA) :有两角及其夹边对应相等的两个三角形全等。
4、角角边(AAS):有两角及一角的对边对应相 等的两个三角形全等。
三、线段中垂线与角平分线的性质
1、 线段垂直平分线的性质:
线段的垂直平分线上的点到线段两端点的距离相等。
几何表述:
∵ 是线段AB的中垂线,点C在L上
∴ CA=CB
2、角平分线的性质:
角平分线上点到角两边距离相等
几何表述:
∵点P是∠BAC的平分线上的一点且PB⊥AB,PC ⊥AC,
∴PB=PC的理由
三、全等概念
记作:“ ABC≌ DEF”
互相重合的顶点叫对应顶点,如A与D
请指出其他的对应顶点:
互相重合的边叫对应边,AB边与DE
请指出其他的对应边:
3、互相重合的角叫对应角,如
请指出其他的对应角:
练习:
、如图,△ABC中,DE垂直平分AC,AE=3cm, △ABC的周长是9cm,则△ABC的周长是_______.
如图,BE、CF是△ABC 的角平分线,∠A=40°。则∠BOC=( )度
3、下列说法正确的是( )
A、有一个外角是钝角的三角形必定是锐角三角形
B、三条线段a,b,c,若满足a>b>c,且a
D、有两条边和一个角对应相等的两个三角形全等
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
