5.6 同底数幂的除法

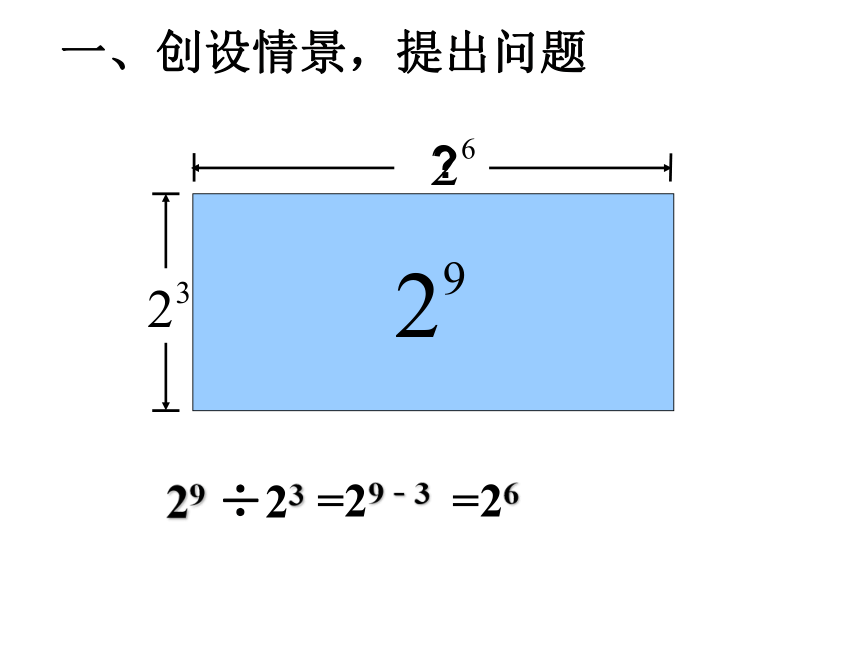
课件13张PPT。5.6 同底数幂的除法(2)?一、创设情景，提出问题 29 ÷23=26=29﹣3 a0=1(a≠0)任何不等于零的数的零次幂都等于1
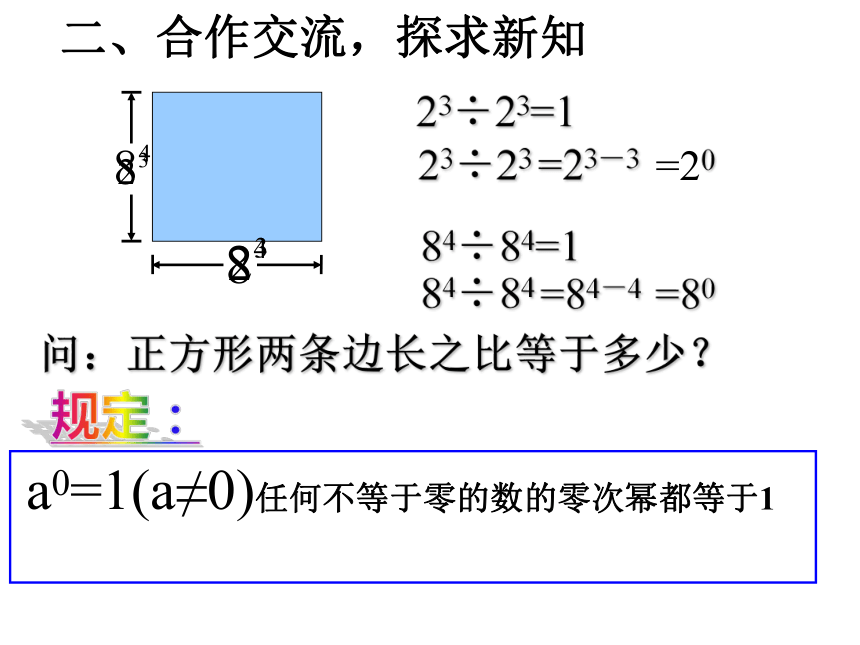
规定：二、合作交流，探求新知 问：正方形两条边长之比等于多少？23÷23=184÷84=123÷23=23－3=2084÷84=84－4=80 任何不等于零的数的-p（p是正整数）次幂，等于这个数的p次幂的倒数。


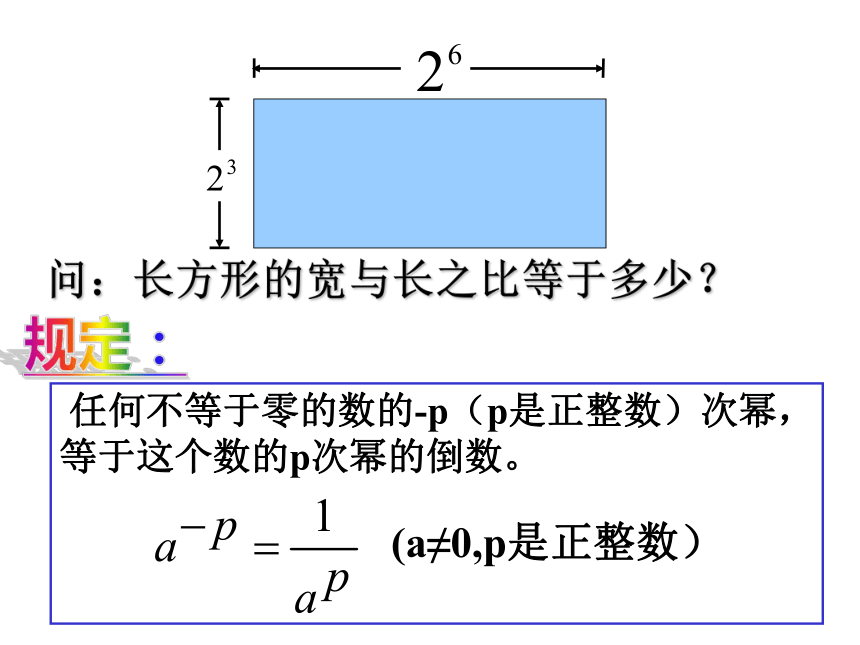
(a≠0,p是正整数）规定：问：长方形的宽与长之比等于多少？理一理：am÷an=am﹣n（a≠0,m,n都是正整数）（1）m＞n（已学过）
（2）m=n
（3）m＜na-p =(a≠0,p是正整数） 规定了零指数幂与负整数指数幂的意义，就把指数从
正整数推广到了整数例3:用分数或整数表示下列各负整数指数幂的值(1) 10-3(2) (-0.5)-3(3) (-3)-4三、发散练习，巩固新知
练习一、××√③（-1）-1=1 （ ）② 8-1=-8 （ ）④ ap×a-p=1(a≠0) （ ）抢答下列计算对吗？为什么？错的请改正。①（-7）0= -1 （ ）×（-7）0= 1 （-1）-1=-1 8-1= 用分数或整数表示下列各负整数指数幂的值:① 100-2 ② (-0.1)-2练习二、③ -30 ④
⑴ a3÷(-10)0
⑵ (-3)5÷36
⑶ a4÷(a3·a2)⑵ 22÷2﹣3⑴ 950×（-5）-1例4 计算：探究拓展100=_____；
10-1=______=_____；
10-2=______=_____；
10-3=______=_____；
10-4=______=_____；
10-5=______=______；填空:10.10.010.0010.00010.00001例5 把下列各数表示成a×10n (1≤a＜10, n为整数）的形式：①12000 ② 0.0021 ③ 0.0000501注意：我们可以用科学记数法表示绝对值较小的数。（1）用科学记数法表示下列各数：② 6 840 000 000① 325 800③ 0.000 129④ 0.000 000 87练习四、（2）用小数表示下列各数：
①1.6×10－3 ②－3.2×10－5四、畅所欲言通过这堂课的学习，你觉得有什么收获！① a0=1（a≠0）
② a－p= （a≠0，p是正整数）
③正整数指数幂的各种运算法则对整数
指数幂都适用
④用科学记数法表示绝对值较小的数 祝同学们 学习进步! 再 见