5.4乘法公式1(平方差公式)
图片预览


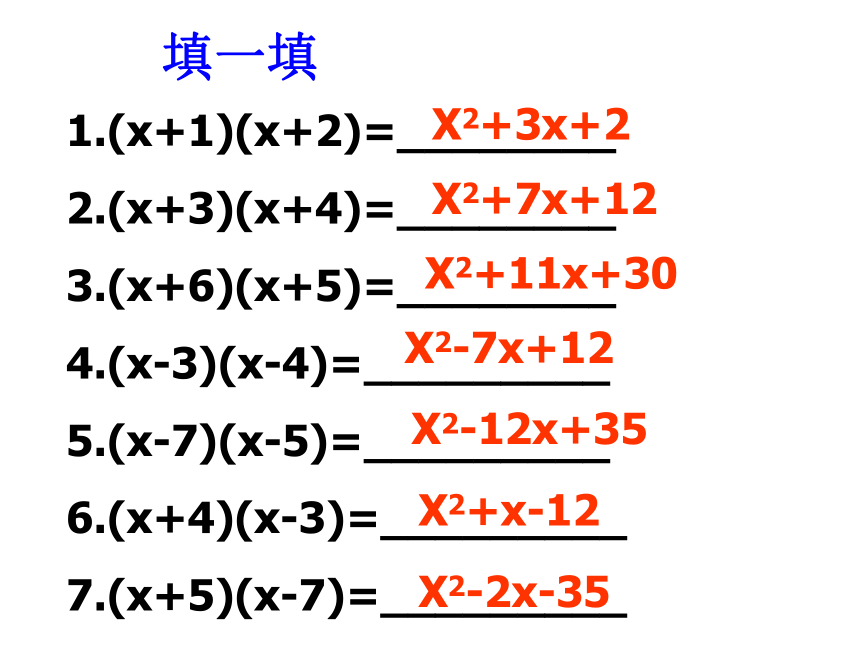


文档简介
课件25张PPT。5.4 乘法公式(1)
(1)、观察下列各式的计算结果与相乘的两个
多项式之间的关系:
(x+2)(x+3)=x2+5x+6
(x+6)(x+5)=x2+11x+30
(1)你发现有什么规律?按你发现的规律填空:
(x+3)(x+5)=x2+( + )x + × (2)、你能很快说出与(x+a)(x+b)的展开式吗?
(x+a) (x+b)=3535x2+(a+b)x+ab观察与探索 1.(x+1)(x+2)=________
2.(x+3)(x+4)=________
3.(x+6)(x+5)=________
4.(x-3)(x-4)=_________
5.(x-7)(x-5)=_________
6.(x+4)(x-3)=_________
7.(x+5)(x-7)=_________X2+3x+2X2+7x+12X2+11x+30X2-7x+12X2-12x+35X2+x-12X2-2x-35填一填 应用: (x+a)(x+b)=x2+(a+b)+ab. 口答 计算下列各题:
(1)(x +2 ) ( x –2 )
(2) (1 +3a ) ( 1 –3a)
(3) (x +5y ) ( x –5y )
(4) ( y –3z ) ( y +3z )= x2 – 4 =1 – 9a2=x2–25 y2= y2 – 9z2= x2 – 22
=1 – (3a)2=x2–(5y)2= y2–(3z)2
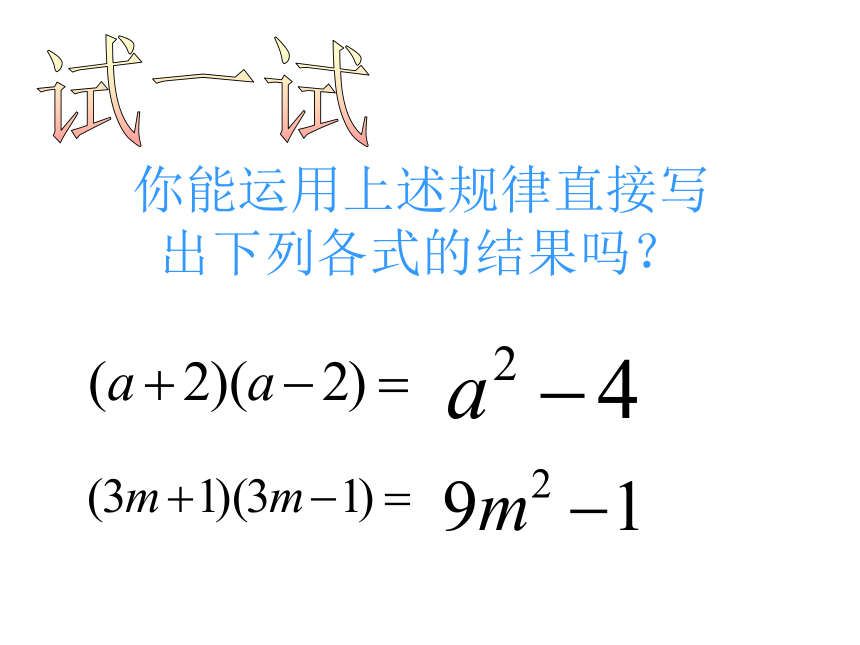
观察以上算式及其结果,你发现了什么规律?平方差公式:( a + b ) ( a – b ) = a 2- b2你能运用上述规律直接写出下列各式的结果吗?试一试 如图:在边长为a的大正方形的一角剪去一个边长为b的小正方形。
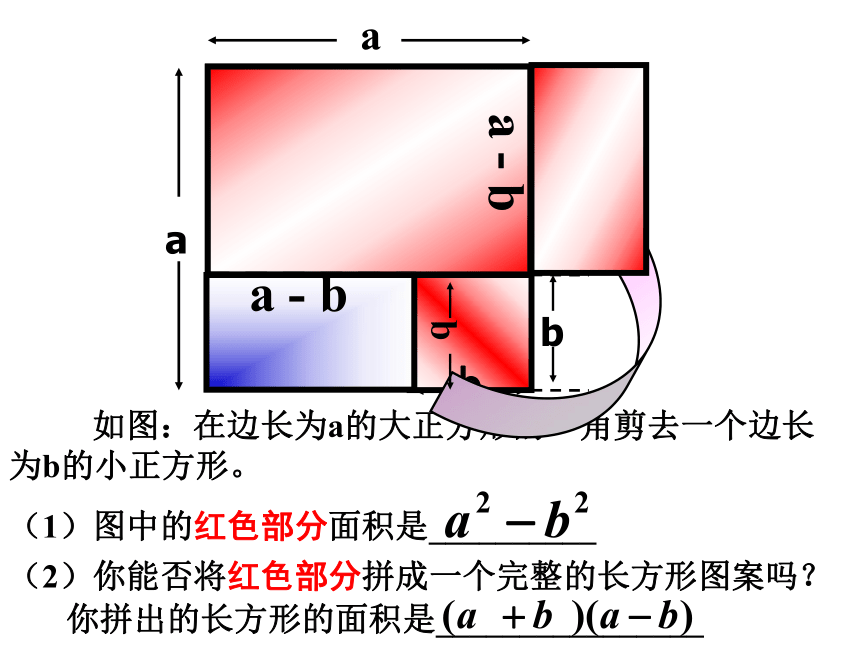
(1)图中的红色部分面积是__________你拼出的长方形的面积是________________
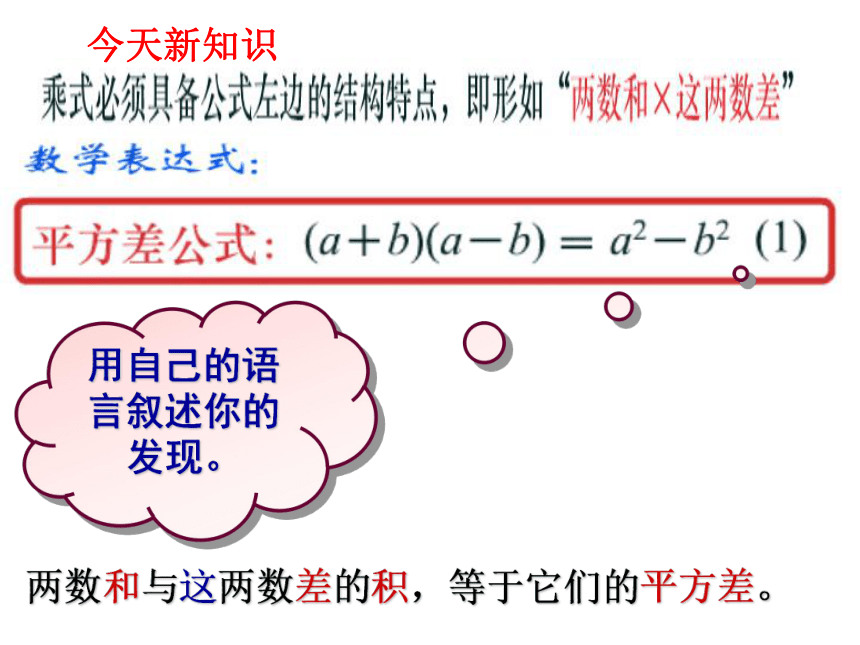
(2)你能否将红色部分拼成一个完整的长方形图案吗?ba - ba - b两数和与这两数差的积,等于它们的平方差。用自己的语言叙述你的发现。今天新知识?
?
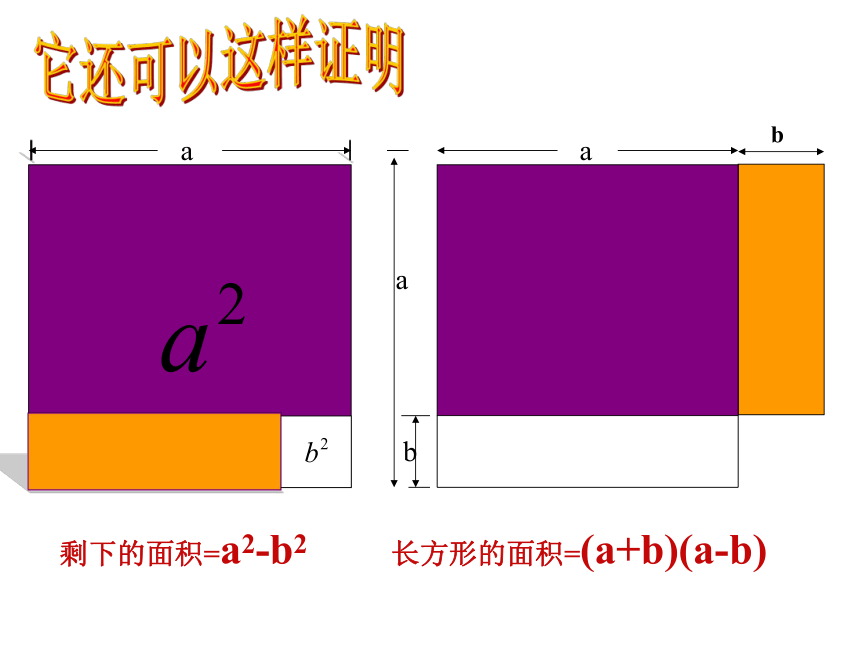
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
它还可以这样证明(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 1.下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 检验成果:××(1) (2x-3y)( )= 4x2-9y2 2x+3y3.填空:(2)( +3a)( -3a)= 4 - 9a2±2 ±2 2( ) 例1:
(1)( 3x+ 5y ) ( 3x- 5y ) (2) (-m + n ) ( -m – n )
(3) ( a+b ) (- a+ b ) (4) ( ab +8) ( ab – 8 )解: (1)原式=(3x)2–(5y)2=9x2–25y2(2)原式=(-m)2–(n)2=m2–n2(3)原式=(b)2–(1/2a)2=b2–1/4a2(4)原式=(ab)2–(8)2=a2b2–64b3aa2-(3b)215b12-(5b)21-25b2-x2(-x)2-22x2-4-2x3(-2x)2-32a2-9b24x2-93b填一填⑴ (a+1)(a-1)=⑵ (3+x)(3-x)=⑶ (a+2b)(a-2b)=⑷ (3x+5y)(3x-5y)=⑸ (10s-3t)(10s+3t)=⑹ (-m+n)(-m-n)=a2-19-x2a2-(2b)2=a2-4b2(3x)2-(5y)2=9x2-25y2(10s)2-(3t)2=100s2-9t2(-m)2-n2=m2-n2接力赛⑺ (-2x-3y) (-2x+3y)=⑽ (-4x+y)(y+4x)=(-2x)2-(3y)2y2-(4x)2=y2-16x2=4x2-9y2问题:利用平方差公式计算的关键是:准确确定a和b怎样确定a与b:符号相同的看作a,符号不同的看作b
接力赛 2、王敏捷同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王敏捷就敏捷地说出应付99.96元,他算得对吗?解决实际问题例2 .计算:103×97解:103×97 =(100+3)(100-3)
=100 2 - 3 2 =10000-9 = 9991 速算PK⑴ 102×98=⑶ 59.8×60.2=⑷ 5678×5680-56792(100+2)(100-2)=9996(60-0.2)(60+0.2)=3599.96=(5679-1)(5679+1)-56792= 56792-1- 56792=-1(1) (x+3)( )=x2-9(2) (-1-2x)( 2x-1)=(3) (m+n)( )=n2-m2(4) ( )(-y-1)=1-y2(5) (-3a2+2b2)( )=9a4-4b4X-31-4x2n-m-1+y-3a2-2b2仔细填一填练习:下列式子中哪些可以用平方差公式运算?⑴ (ab-8)(ab+8) (2) (2+a)(a-2)
(3) (-4k+3)(-4k-3) (4) (1-x)(-x-1)
⑸ (-x-1)(x+1) ⑹ (x+3)(x-2)步骤:1、判断;2、调整;3、用公式。
本节课你学到了什么?两数和与这两数差的积,等于它们的平方差。2.你能很快说出与(x+a)(x+b)的展开式吗?
(x+a) (x+b)=1. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。x2+(a+b)x+ab3.利用公式计算需要注意什么?
你还有什么疑惑吗?布置作业1.必做题:课本第117页 A 组
作业本(1)第25页
2.选做题:课本第117页 B 组 1.化简:代数式 (1-a)(1+a)(1+a2)(1+a4)拓展提高解: 原式=(1–a2)(1+a2)=(1-a4)(1+a4)=1+a8(1+ a4)2.运用平方差公式计算:3.利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1想一想 1. (a+b-c) (a-b-c)
能用平方差公式运算吗?若能,
结果是哪两数的平方差?步骤:1、判断;2、调整;3、用公式。
2. 计算: 99 × 101 × 10001
3. 利用平方差公式计算:
(a+b) 2 - (a-b)2
下列各式能否用平方差公式进行计算⑴ (7ab-3b)(7ab+3b)⑵ (-8+a)(a-8)⑸ (-3-m)(m-3)⑺ (a2+b2)(a2-b2)精心挑一挑⑶⑷ (x+3)(y-3)⑹ (a-b)(b-a)再见
(1)、观察下列各式的计算结果与相乘的两个
多项式之间的关系:
(x+2)(x+3)=x2+5x+6
(x+6)(x+5)=x2+11x+30
(1)你发现有什么规律?按你发现的规律填空:
(x+3)(x+5)=x2+( + )x + × (2)、你能很快说出与(x+a)(x+b)的展开式吗?
(x+a) (x+b)=3535x2+(a+b)x+ab观察与探索 1.(x+1)(x+2)=________
2.(x+3)(x+4)=________
3.(x+6)(x+5)=________
4.(x-3)(x-4)=_________
5.(x-7)(x-5)=_________
6.(x+4)(x-3)=_________
7.(x+5)(x-7)=_________X2+3x+2X2+7x+12X2+11x+30X2-7x+12X2-12x+35X2+x-12X2-2x-35填一填 应用: (x+a)(x+b)=x2+(a+b)+ab. 口答 计算下列各题:
(1)(x +2 ) ( x –2 )
(2) (1 +3a ) ( 1 –3a)
(3) (x +5y ) ( x –5y )
(4) ( y –3z ) ( y +3z )= x2 – 4 =1 – 9a2=x2–25 y2= y2 – 9z2= x2 – 22
=1 – (3a)2=x2–(5y)2= y2–(3z)2
观察以上算式及其结果,你发现了什么规律?平方差公式:( a + b ) ( a – b ) = a 2- b2你能运用上述规律直接写出下列各式的结果吗?试一试 如图:在边长为a的大正方形的一角剪去一个边长为b的小正方形。
(1)图中的红色部分面积是__________你拼出的长方形的面积是________________
(2)你能否将红色部分拼成一个完整的长方形图案吗?ba - ba - b两数和与这两数差的积,等于它们的平方差。用自己的语言叙述你的发现。今天新知识?
?
长方形的面积=(a+b)(a-b)
剩下的面积=a2-b2
它还可以这样证明(1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 1.下列式子可用平方差公式计算吗? 为什么? 如果能够,怎样计算? (不能) (不能) (能) ?(a2 ?b2)= ?a2 + b2 ;(不能) 检验成果:××(1) (2x-3y)( )= 4x2-9y2 2x+3y3.填空:(2)( +3a)( -3a)= 4 - 9a2±2 ±2 2( ) 例1:
(1)( 3x+ 5y ) ( 3x- 5y ) (2) (-m + n ) ( -m – n )
(3) ( a+b ) (- a+ b ) (4) ( ab +8) ( ab – 8 )解: (1)原式=(3x)2–(5y)2=9x2–25y2(2)原式=(-m)2–(n)2=m2–n2(3)原式=(b)2–(1/2a)2=b2–1/4a2(4)原式=(ab)2–(8)2=a2b2–64b3aa2-(3b)215b12-(5b)21-25b2-x2(-x)2-22x2-4-2x3(-2x)2-32a2-9b24x2-93b填一填⑴ (a+1)(a-1)=⑵ (3+x)(3-x)=⑶ (a+2b)(a-2b)=⑷ (3x+5y)(3x-5y)=⑸ (10s-3t)(10s+3t)=⑹ (-m+n)(-m-n)=a2-19-x2a2-(2b)2=a2-4b2(3x)2-(5y)2=9x2-25y2(10s)2-(3t)2=100s2-9t2(-m)2-n2=m2-n2接力赛⑺ (-2x-3y) (-2x+3y)=⑽ (-4x+y)(y+4x)=(-2x)2-(3y)2y2-(4x)2=y2-16x2=4x2-9y2问题:利用平方差公式计算的关键是:准确确定a和b怎样确定a与b:符号相同的看作a,符号不同的看作b
接力赛 2、王敏捷同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王敏捷就敏捷地说出应付99.96元,他算得对吗?解决实际问题例2 .计算:103×97解:103×97 =(100+3)(100-3)
=100 2 - 3 2 =10000-9 = 9991 速算PK⑴ 102×98=⑶ 59.8×60.2=⑷ 5678×5680-56792(100+2)(100-2)=9996(60-0.2)(60+0.2)=3599.96=(5679-1)(5679+1)-56792= 56792-1- 56792=-1(1) (x+3)( )=x2-9(2) (-1-2x)( 2x-1)=(3) (m+n)( )=n2-m2(4) ( )(-y-1)=1-y2(5) (-3a2+2b2)( )=9a4-4b4X-31-4x2n-m-1+y-3a2-2b2仔细填一填练习:下列式子中哪些可以用平方差公式运算?⑴ (ab-8)(ab+8) (2) (2+a)(a-2)
(3) (-4k+3)(-4k-3) (4) (1-x)(-x-1)
⑸ (-x-1)(x+1) ⑹ (x+3)(x-2)步骤:1、判断;2、调整;3、用公式。
本节课你学到了什么?两数和与这两数差的积,等于它们的平方差。2.你能很快说出与(x+a)(x+b)的展开式吗?
(x+a) (x+b)=1. 试用语言表述平方差公式 (a+b)(a?b)=a2?b2。x2+(a+b)x+ab3.利用公式计算需要注意什么?
你还有什么疑惑吗?布置作业1.必做题:课本第117页 A 组
作业本(1)第25页
2.选做题:课本第117页 B 组 1.化简:代数式 (1-a)(1+a)(1+a2)(1+a4)拓展提高解: 原式=(1–a2)(1+a2)=(1-a4)(1+a4)=1+a8(1+ a4)2.运用平方差公式计算:3.利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1想一想 1. (a+b-c) (a-b-c)
能用平方差公式运算吗?若能,
结果是哪两数的平方差?步骤:1、判断;2、调整;3、用公式。
2. 计算: 99 × 101 × 10001
3. 利用平方差公式计算:
(a+b) 2 - (a-b)2
下列各式能否用平方差公式进行计算⑴ (7ab-3b)(7ab+3b)⑵ (-8+a)(a-8)⑸ (-3-m)(m-3)⑺ (a2+b2)(a2-b2)精心挑一挑⑶⑷ (x+3)(y-3)⑹ (a-b)(b-a)再见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
