第六章 因式分解的复习课
图片预览









文档简介
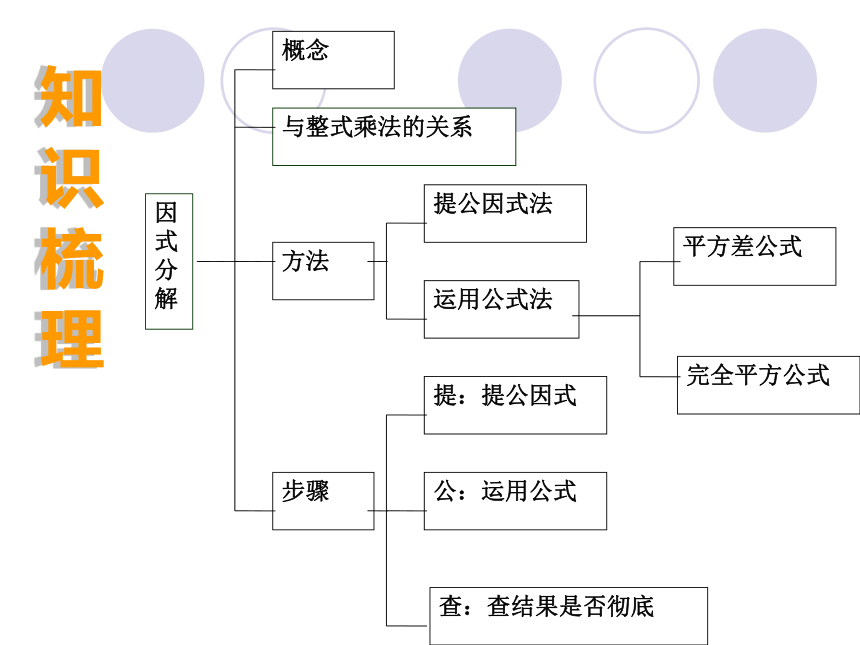
课件33张PPT。第六章因式分解复习课知 识 梳 理 平方差公式a2-b2=(a+b)(a-b)
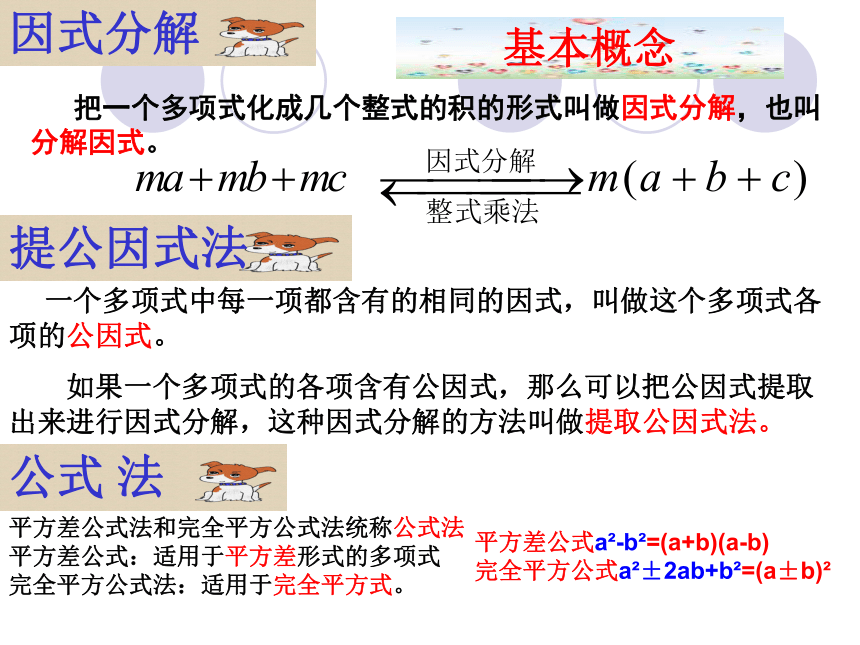
完全平方公式a2±2ab+b2=(a±b)2 把一个多项式化成几个整式的积的形式叫做因式分解,也叫分解因式。
一个多项式中每一项都含有的相同的因式,叫做这个多项式各项的公因式。
如果一个多项式的各项含有公因式,那么可以把公因式提取出来进行因式分解,这种因式分解的方法叫做提取公因式法。平方差公式法和完全平方公式法统称公式法
平方差公式:适用于平方差形式的多项式
完全平方公式法:适用于完全平方式。公式 法因式分解基本概念提公因式法1.公因式确定
(1)系数:取各系数的最大公约数;
(2)字母:取各项相同的字母;
(3)相同字母的指数:取最低指数。
2.变形规律:
(1)x-y=-(y-x) (2) -x-y=-(x+y)
(3) (x-y)2=(y-x)2 (4) (x-y)3=-(y-x)3
3.一般步骤
(1)确定应提取的公因式;
(2)多项式除以公因式,所得的商作为另一个因式;
(3)把多项式写成这两个因式的积的形式。提公因式法:用平方差公式分解因式的关键:多项式是否能看成两个数的平方的差;
用完全平方公式分解因式的关键:在于判断一个多项式是否为一个完全平方式;
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
公式法因式分解的一般步骤:一提:先看多项式各项有无公因式,如有公因式则要先提取公因式;二套:再看有几项,
如两项,则考虑用平方差公式;如三项,则考虑用完全平方公 式;四查:最后用整式乘法检验一遍,并看各因式能否再分解,如能分解,应分解到不能再分解为止。三变:若以上两步都不行,则将考虑将多项式变形,使之能“提”或能“套”。[如(x+y)2-x-y=(x+y)(x+y-1)因式分解的应用2,若A·B=0,则 A=0或B=01,运用因式分解进行多项式除法3, 运用因式分解解简单的方程否否是A层练习
下列代数式的变形当中哪些是因式分解,哪些不是?
(1)3a2+6a=3a(a+2)
(2)(2y+1)(2y-1)=4y2-1
(3) 18a3bc=3a2b·6ac 是不是?
是不是?
是不是?基本概念(4) X2+2X+1=X(X+2)+1
(5) a2+1=a(a+1/a). 是不是?否是不是?否否是否是B层练习
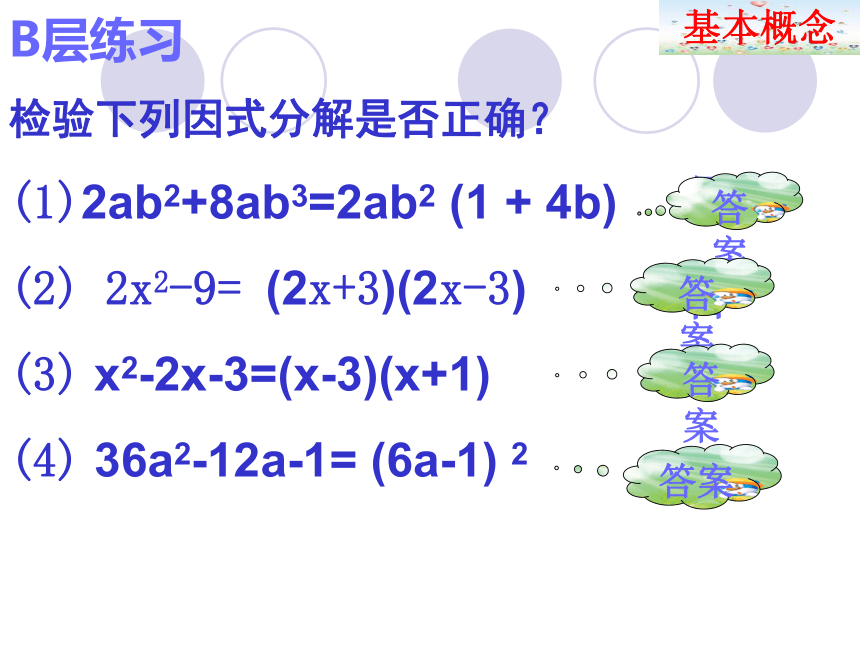
检验下列因式分解是否正确?
(1)2ab2+8ab3=2ab2 (1 + 4b)
(2) 2x2-9= (2x+3)(2x-3)
(3) x2-2x-3=(x-3)(x+1)
(4) 36a2-12a-1= (6a-1) 2答案答案答案答案基本概念C层练习
填空
1.若 x2+mx-n能分解成(x-2)(x-5),则m=???? ,n=??? ??。
2.x2-8x+m=(x-4)(???? ),且m=?? ??。 -7-10x-416基本概念A层练习
将下列各式分解因式:
⑴ -a2-ab;
⑵ m2-n2;
⑶ x2+2xy+y2
(4) 3am2-3an2;
(5) 3x3+6x2y+3xy2
基本方法=-a(a+b)= (m+n)(m-n)=(x+y)2=3a (m+n)(m-n)=3x(x+y)2B层练习
将下列各式分解因式:
⑴ 18a2c-8b2c
⑵ m4 - 81n4
⑶ x2y2-4xy+4基本方法=2c(3a+2b) (3a-2b)= (m2 +9n2)(m+3n) (m-3n)=(x y –2)2C层练习
将下列各式分解因式:
⑴ (2a+b)2–(a–b)2 ;
(2) (x+y)2-10(x+y)+25
(3) 4a2–3b(4a–3b)
基本方法= (2a- 3 b) 2= (x+y-5)2=3a (a+2b)简化计算 (1)562+56×44 (2)9992 - 9982
变式
若a=99,b=-1,则a2-2ab+b2=____________;基本应用解方程:x3-9x=0变式
解下列方程:
(3x- 4) 2- (3x+ 4) 2=48
基本应用例1:有关完全平方式的运用1.若9x2+mx+16是完全平方式,则m= .
2.若x2-6xy+m,是完全平方式,则m= .
3.若x2-x+m2,是完全平方式,则m= .
4.若x2+25与一个单项式的和是一个完全平方式,则这个单项式可以是 .
典例解析:例2:因式分解的应用1.简便计算
(1)
(2) 5×102004-102005
(3)9992-1002×998
(4)19992-3994×1999+19972
(5)20062-20052+20042-20032+…+22-1典例解析:2.条件式计算
(1) 若2b-a=-3,ab=5,
则2a2b-4ab2的值是 .
(2) 若∣2x-y+5∣+(x+2y-4)2=0,
则(2x-y)3-(x-3y)(y-2x)2的值是 .
(3) 若(A+2005)2=987654321,
则(A+2015)(A+1995)的值是 .
(4) 若(a2 +b2)(a2 +b2-2)=-1,
则a2 +b2的值是 .
(5) 若4a2+b2+4a-6b+10=0,
则a3b-ab3的值是 .
例3:因式分解的应用典例解析:例4:多项式除法1.(4x2-12xy+9y2) ÷(3y-2x)
2.(-a+9a3) ÷(3a-1)
3.[(x+3y)2-4x2]÷(x+y)典例解析:练一练: A层练习:
⑴ 12am2-3an2; ⑵ 3x3+6x2y+3xy2
B层练习:
⑴ 18a2c-8b2c; ⑵ m4 - 81n4 ;
⑶ x2 - 4x(x -y)+ 4(x -y)2 ;
C层练习:
⑴ (2a+b)2–(a–b)2 ; ⑵ 4a2–3b(4a–3b); 各小组解答后请组内四位同学进行相互交流并订正!1、将下列各式分解因式:(1) 7x2+2x=0
2.解方程:(2) 2x2=(2x-5)2若AB=0
则A=0或
B=0
方法:
左边为0,
右边进行因
式分解。
练一练:3.计算:
(1) (2mp-3mq+4mr) ÷(2p-3q+4r)
(2) [(3x-7)2-(x+5)2] ÷(4x-24)练一练:今天这节课,复习归纳了哪些知识?
你有哪些收获与感受?
说出来大家分享。 课堂小结:1、课后目标与评定
2、作业本复习题作业:1.(2008年广州)分解因式:
2.(2007年遵义)分解因式:
3.(2004年盐城)分解因式:4.(2005年济南)分解因式: 5.(2006年南京)在实数范围内分解因式:6.(2003年济南)分解因式:7.(2009年遵义)因式分解:3x(x-2)-(2-x)=__________中考零接近1.(2006年荆州)分解因式:2.(2006年潜江)分解因式: 3.(2006年黄冈)将 分解因式,结果为__________. 4.(2006年湖州)分解因式:5.(2006年安徽)因式分解:6.(2009年杭州)实数范围内因式分解:
练一练8.(2004年南平)分解因式:7.(2004年陕西)分解因式:
9.(2003年巴中)分解因式:11.(2004年甘肃)为使 在整数范围内可以分解因式,则可能取的值是________.(任写一个)10.(2003年湖南)已知 在有理数范围内能分解成两个因式的积,则正整数的值是________.12.(2004年金华中考)如果二次三项式 在整数范围内可以分解因式,那么整数a的取值是(只需填写一个你认为正确的答案即可)_______.
14.(2005年山西中考)在多项式 中,添加一个单项式,使其成为一个完全平方式。则添加的单项式是________________.
13.(2003年黄冈)若 ,则 m=_______.n=_______,
此时将 分解因式得______________。
1.(2003年安徽)下列多项式能分解因式的是( )
B.
C. D.2. (2004年安徽)下列多项式中,能用提取公因式
分解因式的是( )
A. B.
C. D.
3.(2005年茂名)下列各式由左边到右边的变形中,
是分解因式的是( )
A.a(x+y)=ax+ay B.
C. D.选一选4.(2006年北京)把多项式 分解因式,
结果正确的是( )
A. B.
C. x(y+3)(y-3) D.x(y+9)(y-9)5.(2006年株洲)(3a-y)(3a+y)是下列哪一个
多项式 因式分解的结果为( )
A. B. C. D.6.(2000年安徽)下列多项式中,能用公式法
分解因式的是( )
A. B.
C. D.
7.(2005年济南)利用因式分解简便计算:
57×99+44×99-99正确的是( )
A.99×(57+44)=99×101=9999
B.99×(57+44-1)=99×100=9900
C.99×(57+44+1)=99×102=10098
D.99×(57+44-99)=99×2=198.8.(2005年盐城)下列因式分解中,结果正确的是( )
A. B.
C. D.1. (2006年济南中考)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解。
, , 1 ,
2.(2003年黄石)若
是完全平方式,求a的值。再 见
完全平方公式a2±2ab+b2=(a±b)2 把一个多项式化成几个整式的积的形式叫做因式分解,也叫分解因式。
一个多项式中每一项都含有的相同的因式,叫做这个多项式各项的公因式。
如果一个多项式的各项含有公因式,那么可以把公因式提取出来进行因式分解,这种因式分解的方法叫做提取公因式法。平方差公式法和完全平方公式法统称公式法
平方差公式:适用于平方差形式的多项式
完全平方公式法:适用于完全平方式。公式 法因式分解基本概念提公因式法1.公因式确定
(1)系数:取各系数的最大公约数;
(2)字母:取各项相同的字母;
(3)相同字母的指数:取最低指数。
2.变形规律:
(1)x-y=-(y-x) (2) -x-y=-(x+y)
(3) (x-y)2=(y-x)2 (4) (x-y)3=-(y-x)3
3.一般步骤
(1)确定应提取的公因式;
(2)多项式除以公因式,所得的商作为另一个因式;
(3)把多项式写成这两个因式的积的形式。提公因式法:用平方差公式分解因式的关键:多项式是否能看成两个数的平方的差;
用完全平方公式分解因式的关键:在于判断一个多项式是否为一个完全平方式;
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式:a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
公式法因式分解的一般步骤:一提:先看多项式各项有无公因式,如有公因式则要先提取公因式;二套:再看有几项,
如两项,则考虑用平方差公式;如三项,则考虑用完全平方公 式;四查:最后用整式乘法检验一遍,并看各因式能否再分解,如能分解,应分解到不能再分解为止。三变:若以上两步都不行,则将考虑将多项式变形,使之能“提”或能“套”。[如(x+y)2-x-y=(x+y)(x+y-1)因式分解的应用2,若A·B=0,则 A=0或B=01,运用因式分解进行多项式除法3, 运用因式分解解简单的方程否否是A层练习
下列代数式的变形当中哪些是因式分解,哪些不是?
(1)3a2+6a=3a(a+2)
(2)(2y+1)(2y-1)=4y2-1
(3) 18a3bc=3a2b·6ac 是不是?
是不是?
是不是?基本概念(4) X2+2X+1=X(X+2)+1
(5) a2+1=a(a+1/a). 是不是?否是不是?否否是否是B层练习
检验下列因式分解是否正确?
(1)2ab2+8ab3=2ab2 (1 + 4b)
(2) 2x2-9= (2x+3)(2x-3)
(3) x2-2x-3=(x-3)(x+1)
(4) 36a2-12a-1= (6a-1) 2答案答案答案答案基本概念C层练习
填空
1.若 x2+mx-n能分解成(x-2)(x-5),则m=???? ,n=??? ??。
2.x2-8x+m=(x-4)(???? ),且m=?? ??。 -7-10x-416基本概念A层练习
将下列各式分解因式:
⑴ -a2-ab;
⑵ m2-n2;
⑶ x2+2xy+y2
(4) 3am2-3an2;
(5) 3x3+6x2y+3xy2
基本方法=-a(a+b)= (m+n)(m-n)=(x+y)2=3a (m+n)(m-n)=3x(x+y)2B层练习
将下列各式分解因式:
⑴ 18a2c-8b2c
⑵ m4 - 81n4
⑶ x2y2-4xy+4基本方法=2c(3a+2b) (3a-2b)= (m2 +9n2)(m+3n) (m-3n)=(x y –2)2C层练习
将下列各式分解因式:
⑴ (2a+b)2–(a–b)2 ;
(2) (x+y)2-10(x+y)+25
(3) 4a2–3b(4a–3b)
基本方法= (2a- 3 b) 2= (x+y-5)2=3a (a+2b)简化计算 (1)562+56×44 (2)9992 - 9982
变式
若a=99,b=-1,则a2-2ab+b2=____________;基本应用解方程:x3-9x=0变式
解下列方程:
(3x- 4) 2- (3x+ 4) 2=48
基本应用例1:有关完全平方式的运用1.若9x2+mx+16是完全平方式,则m= .
2.若x2-6xy+m,是完全平方式,则m= .
3.若x2-x+m2,是完全平方式,则m= .
4.若x2+25与一个单项式的和是一个完全平方式,则这个单项式可以是 .
典例解析:例2:因式分解的应用1.简便计算
(1)
(2) 5×102004-102005
(3)9992-1002×998
(4)19992-3994×1999+19972
(5)20062-20052+20042-20032+…+22-1典例解析:2.条件式计算
(1) 若2b-a=-3,ab=5,
则2a2b-4ab2的值是 .
(2) 若∣2x-y+5∣+(x+2y-4)2=0,
则(2x-y)3-(x-3y)(y-2x)2的值是 .
(3) 若(A+2005)2=987654321,
则(A+2015)(A+1995)的值是 .
(4) 若(a2 +b2)(a2 +b2-2)=-1,
则a2 +b2的值是 .
(5) 若4a2+b2+4a-6b+10=0,
则a3b-ab3的值是 .
例3:因式分解的应用典例解析:例4:多项式除法1.(4x2-12xy+9y2) ÷(3y-2x)
2.(-a+9a3) ÷(3a-1)
3.[(x+3y)2-4x2]÷(x+y)典例解析:练一练: A层练习:
⑴ 12am2-3an2; ⑵ 3x3+6x2y+3xy2
B层练习:
⑴ 18a2c-8b2c; ⑵ m4 - 81n4 ;
⑶ x2 - 4x(x -y)+ 4(x -y)2 ;
C层练习:
⑴ (2a+b)2–(a–b)2 ; ⑵ 4a2–3b(4a–3b); 各小组解答后请组内四位同学进行相互交流并订正!1、将下列各式分解因式:(1) 7x2+2x=0
2.解方程:(2) 2x2=(2x-5)2若AB=0
则A=0或
B=0
方法:
左边为0,
右边进行因
式分解。
练一练:3.计算:
(1) (2mp-3mq+4mr) ÷(2p-3q+4r)
(2) [(3x-7)2-(x+5)2] ÷(4x-24)练一练:今天这节课,复习归纳了哪些知识?
你有哪些收获与感受?
说出来大家分享。 课堂小结:1、课后目标与评定
2、作业本复习题作业:1.(2008年广州)分解因式:
2.(2007年遵义)分解因式:
3.(2004年盐城)分解因式:4.(2005年济南)分解因式: 5.(2006年南京)在实数范围内分解因式:6.(2003年济南)分解因式:7.(2009年遵义)因式分解:3x(x-2)-(2-x)=__________中考零接近1.(2006年荆州)分解因式:2.(2006年潜江)分解因式: 3.(2006年黄冈)将 分解因式,结果为__________. 4.(2006年湖州)分解因式:5.(2006年安徽)因式分解:6.(2009年杭州)实数范围内因式分解:
练一练8.(2004年南平)分解因式:7.(2004年陕西)分解因式:
9.(2003年巴中)分解因式:11.(2004年甘肃)为使 在整数范围内可以分解因式,则可能取的值是________.(任写一个)10.(2003年湖南)已知 在有理数范围内能分解成两个因式的积,则正整数的值是________.12.(2004年金华中考)如果二次三项式 在整数范围内可以分解因式,那么整数a的取值是(只需填写一个你认为正确的答案即可)_______.
14.(2005年山西中考)在多项式 中,添加一个单项式,使其成为一个完全平方式。则添加的单项式是________________.
13.(2003年黄冈)若 ,则 m=_______.n=_______,
此时将 分解因式得______________。
1.(2003年安徽)下列多项式能分解因式的是( )
B.
C. D.2. (2004年安徽)下列多项式中,能用提取公因式
分解因式的是( )
A. B.
C. D.
3.(2005年茂名)下列各式由左边到右边的变形中,
是分解因式的是( )
A.a(x+y)=ax+ay B.
C. D.选一选4.(2006年北京)把多项式 分解因式,
结果正确的是( )
A. B.
C. x(y+3)(y-3) D.x(y+9)(y-9)5.(2006年株洲)(3a-y)(3a+y)是下列哪一个
多项式 因式分解的结果为( )
A. B. C. D.6.(2000年安徽)下列多项式中,能用公式法
分解因式的是( )
A. B.
C. D.
7.(2005年济南)利用因式分解简便计算:
57×99+44×99-99正确的是( )
A.99×(57+44)=99×101=9999
B.99×(57+44-1)=99×100=9900
C.99×(57+44+1)=99×102=10098
D.99×(57+44-99)=99×2=198.8.(2005年盐城)下列因式分解中,结果正确的是( )
A. B.
C. D.1. (2006年济南中考)请你从下列各式中,任选两式作差,并将得到的式子进行因式分解。
, , 1 ,
2.(2003年黄石)若
是完全平方式,求a的值。再 见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
