7.4 分式方程

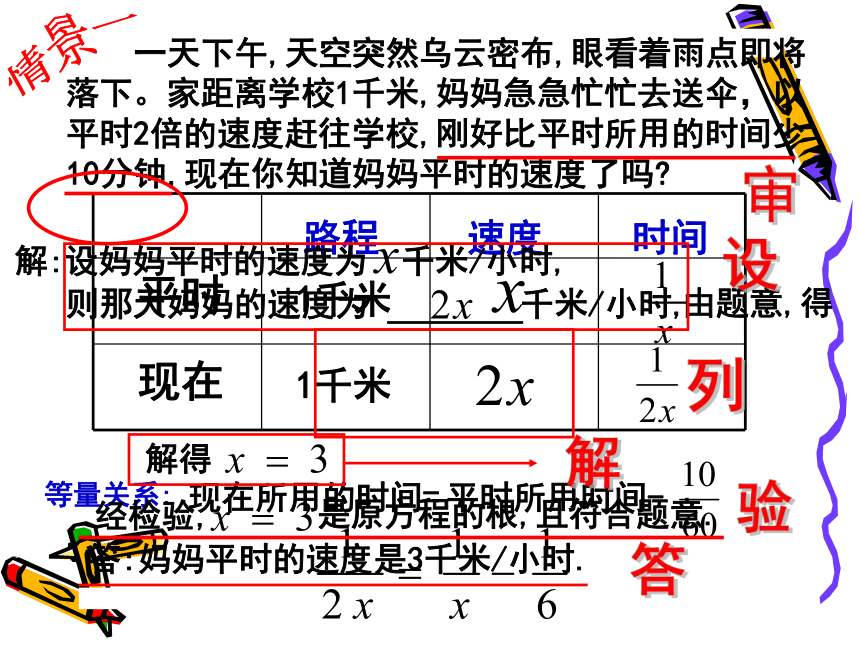
课件16张PPT。7.4分式方程的应用确定最简公分母,去分母,化为一元一次整式两边同乘以 得:把x=-3代入最简公分母检验:(x-2)(1-x)(1+x) =-8解：所以 X=-3所以X=-3是原方程的根。回顾 一天下午,天空突然乌云密布,眼看着雨点即将落下。家距离学校1千米,妈妈急急忙忙去送伞，以平时2倍的速度赶往学校,刚好比平时所用的时间少10分钟,现在你知道妈妈平时的速度了吗?路程时间速度现在平时1千米1千米等量关系:现在所用的时间=由题意,得解得答:妈妈平时的速度是3千米/小时.审设列解验答情景一用分式方程解决实际问题的一般步骤:1.审:2.设:3.列:4.解:认真仔细.5.验:6.答:不要忘记写.分析题意,找出研究对象,建立等量关系.选择恰当的未知数,注意单位.根据等量关系正确列出方程.验是否为增根,是否符合题意.成本售价毛利率改进工艺前改进工艺后2售价=成本+利润利润=成本×毛利率2.525%25%+15%2.5毛利率=售价-成本成本×100%解:设这种原料的成本降低了X元,2×(1+25%)=2.5由题意,得解这个方程,得答:原料降低了0.21元.改进工艺后成本为 元,2-X妈妈为了增加收入,决定做手工艺品,原料的成本为2元,毛利率为25%,后来该工厂通过改进工艺,降低了成本,在售价不变的情况下,毛利率增加了15%.问这种原料的成本降低了多少元(精确到0.01元)? 情景二 放假回家以后,你和妈妈一起做手工艺品,你和妈妈一起做,每小时可做35个,同时做,当你做90个时,妈妈做了120个,问你和妈妈每时各做多少个手工艺品?情景三 在行程问题中，路程s与速度v，时间t之间的关系是什么？公式变形下面的公式变形对吗？如果不对，应怎样改正？
解：由 ，得
即b＝a+将公式 （1+ax≠0）变形成
已知x，a，求b公式变形例2： 照相机成像应用了一个重要原理，即
(v≠f)，
其中 f 表示照相机镜头的焦距，u 表示物体到镜头的距离，v 表示明胶片（像）到镜头的距离，如果一架照相机 f 已固定，那么就要依靠调整 u、v 来使成像清晰，问在 f、v 已知的情况下，怎样确定物体到镜头的距离u？分析：本题就是利用解分式方程把已知公式变形。
把f、v看成已知数，u看成未知数，解关于u的分式方程。解 把f,v均看做已知数，解以u为未知数的方程：移项，得∴当f≠v时，检验：因为v,f不为零，f≠v,所以 ，是分式方程 的根.答：在已知f,v的情况下，物体到镜头的距离u可以由公式 来确定.例题解析 某市从今年1月1日起调整居民用水价格,每m3水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5m3,求我市今年居民用水的价格?此题的等量关系有哪些？×(1+ax≠0)∴∴ab=下面的公式变形对吗？如果不对，应怎样改正？25%25%＋15%2分析:例1、工厂生产一种电子配件，每只的成本为2元，毛利率为25%；后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%．问这种配件每只的成本降低了多少元？（精确到0.01元）设这种配件每只的成本降低了x元(2-x)2×(1+25%)2.5例1、工厂生产一种电子配件，每只的成本为2元，毛利率为25%；后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%．问这种配件每只的成本降低了多少元？（精确到0.01元）解:设这种配件每只的成本降低了x元.根据题意得:解这个方程，得≈0.21答：每只成本降低了0.21元检验 例3：工厂生产一种电子配件，每只的成本为2元，毛利率为25%，后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，问这种配件每只的成本降低了多少元？（精确到0.01元）本题等量关系是什么？例题解析毛利润＝售价－成本25%25%＋15%2试一试：