第七章 分式 复习

课件19张PPT。第七章 分式复习分式的概念、性质分式方程及其应用分式的乘除、加减(1)根据规律可知第5个数应是 ,1.观察下面一列有规律的数： ___ , …(2)可知第n个数应是 (n为正整数)基础回顾(3) 是什么代数式? 这种代数式有什么特征? 分式有意义的条件:B≠0 分式无意义的条件:B = 0 分式值为 0 的条件:A = 0 且 B ≠0知识梳理形如 ,其中A ,B都是整式, 且B中含有字母.1、分式:①表示两个整式相除，
②除式中要含有字母．典型例题1.当_______时，分式 无意义。2.当_______时，分式 有意义。3.当_______时，分式 的值为零。4.若分式 的值是整数，
则整数x可取的值有___________。0,-2, 2,-45.在代数式：



中，分式共有_____个。36、当x=2时,分式 没有意义,
则 b=______ -47、已知分式当_______________时,分式有意义;
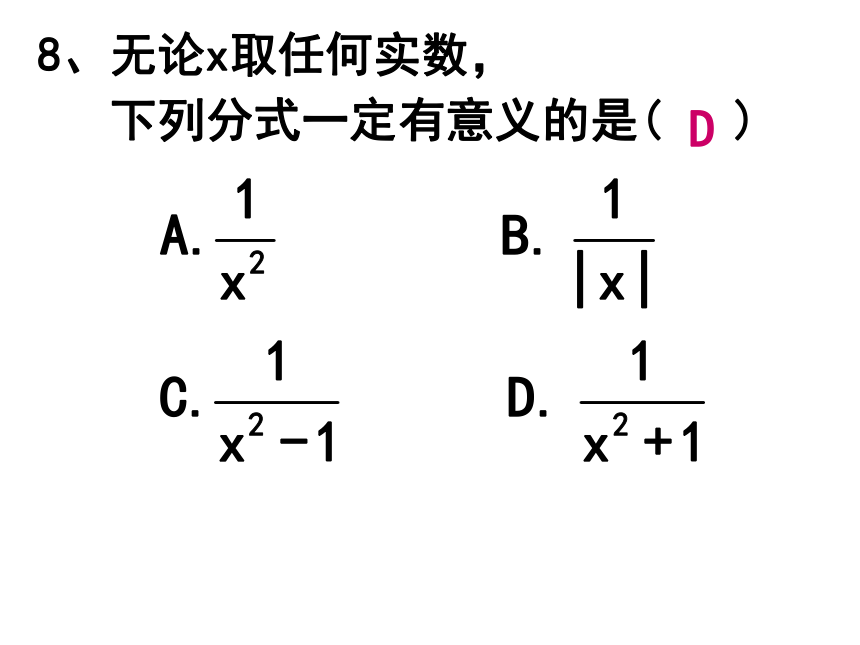
当_______________时,分式的值是零;8、无论x取任何实数，
下列分式一定有意义的是( )D知识梳理2.分式的基本性质：3.分式的符号法则：典型例题应用一分子、分母系数化整.应用二最高次项的系数都化为正数.应用三化简分式.典型例题1.不改变分式的值，把下列分式的分子与分母的最高次项的系数都化为正数。2、 中的分子、分母的x，y同时 扩大2倍， 则分式的值_______;把分式 中的分子、分母的x，y同时扩大2倍，则分式的值____________;
典型例题不变是原来的2倍知识梳理 4.分式的约分与通分：约分的关键：确定分子和分母的公因式。
通分的关键：找到最简公分母。 5.分式的乘除与加减：知识梳理1.同分母分式相加减:2.异分母分式加减步骤：
(1)找公分母；
(2)通分；
(3)转化为同分母加减的法则计算并化简
(确定公分母的方法:一般取各分母系数的最小公倍数与各分母各个因式的最高次幂的积为公分母)1．计算： ＝　　　　　．2.分式 的最简公分母是_______________1练习巩固3．计算： =_______知识梳理 6.分式方程：三步骤：两边同乘各分式的最简公分母。
解整式方程。
检验。 7.应用分式方程解决实际问题：关键：仔细分析各种量之间的关 系，灵活设未知数；找等量关系。
注意：两个检验。1、下列方程中，是分式方程（ ）C典型例题分式方程必须检验,若有增根,要舍去找出公分母典型例题1.解方程：2.当m为何值时，去分母解方程
会产生增根x=2？解 方程两边同时乘以(x+2)(x-2) ，得当x=2时，所以，当m为-4时,去分母解方程会产生增根.课后练习1、计算：2、解方程：