《杨辉三角和两数和的乘方》综合实践活动课
文档属性
| 名称 | 《杨辉三角和两数和的乘方》综合实践活动课 |
|
|
| 格式 | rar | ||
| 文件大小 | 58.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-26 00:00:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
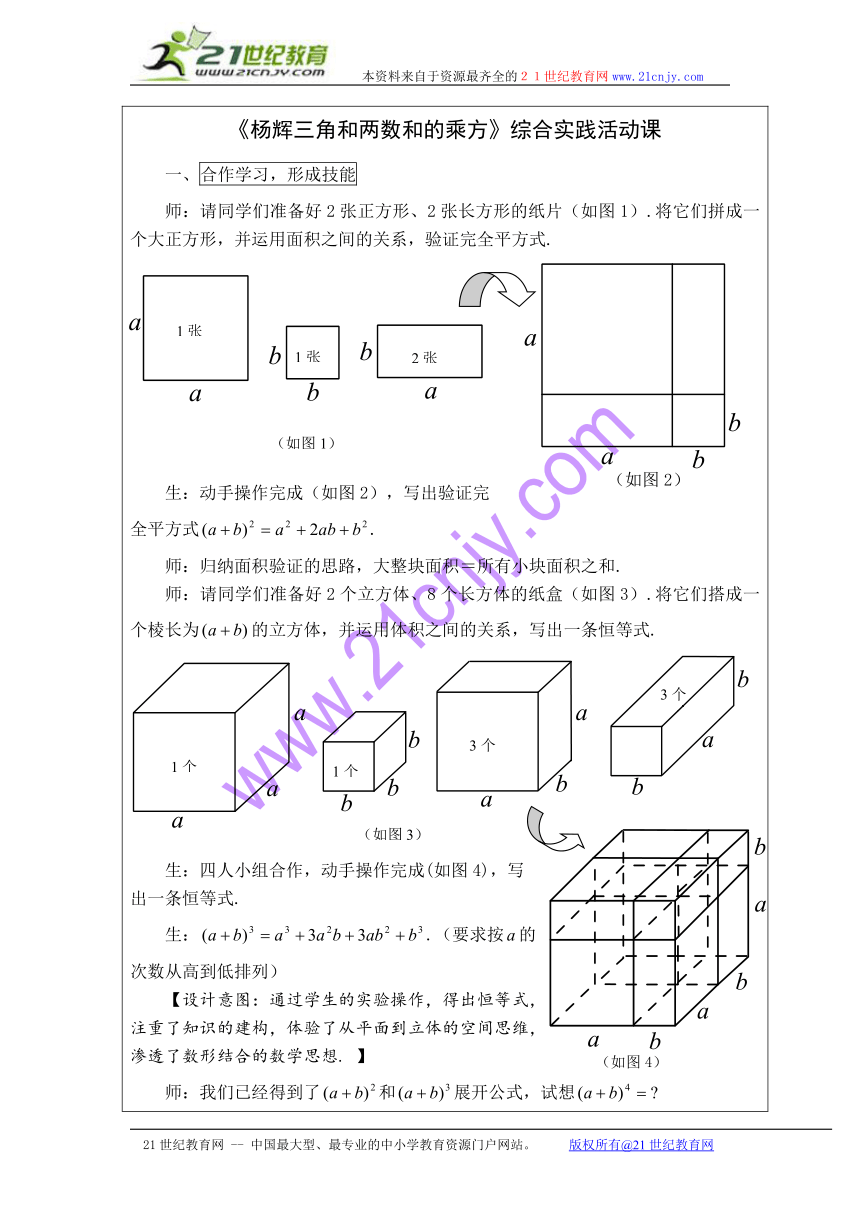
《杨辉三角和两数和的乘方》综合实践活动课一、合作学习,形成技能师:请同学们准备好2张正方形、2张长方形的纸片(如图1).将它们拼成一个大正方形,并运用面积之间的关系,验证完全平方式. 生:动手操作完成(如图2),写出验证完全平方式.师:归纳面积验证的思路,大整块面积=所有小块面积之和.师:请同学们准备好2个立方体、8个长方体的纸盒(如图3).将它们搭成一个棱长为的立方体,并运用体积之间的关系,写出一条恒等式.生:四人小组合作,动手操作完成(如图4),写出一条恒等式.生:.(要求按的次数从高到低排列)【设计意图:通过学生的实验操作,得出恒等式,注重了知识的建构,体验了从平面到立体的空间思维,渗透了数形结合的数学思想. 】师:我们已经得到了和展开公式,试想生:学生先独立完成,然后同桌讨论交流. 生1:生2:师:我们也知道下面将计算结果中各展开式的每项系数排列成下表(简称系数表): 1 1 1 2 1 1 3 3 1 1 4 6 4 1师:因上表形如三角形,我国古代数学家杨辉对其有过深入研究,所以称它为杨辉三角,并提出课题.【设计意图:通过合作学习,从不同角度训练学生的思维,既提高学生学习兴趣,又培养合作团队精神和创造能力. 】二、介绍杨辉,感受成就杨辉,杭州钱塘人。中国南宋末年数学家,数学教育家.著作甚多,他编著的数学书共五种二十一卷,著有《详解九章算法》十二卷(1261年)、《日用算法》二卷、《乘除通变本末》三卷、《田亩比类乘除算法》二卷、《续古摘奇算法》二卷.其中后三种合称《杨辉算法》,朝鲜、日本等国均有译本出版,流传世界.
“杨辉三角”出现在杨辉编著的《详解九章算法》一书中,该书还说明此表源于我国北宋数学家贾宪(约公元11世纪)的“开方作法本源图”,这表明我国发现这个表不晚于11世纪.因此,我们把此表叫杨辉三角或贾宪三角.在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的(Blaise Pascal, 1623年~1662年),他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.【设计意图:了解数学家杨辉及其成就, 增强民族自豪感;让学生体会到研究杨辉三角就是体察杨辉的探索精神,以鼓励学生探究的热情. 】三、探求规律,形成新知1 1 1 2 1 1 3 3 1 1 4 6 4 1 师:(1)请你找出上述数据上下行之间的规律.(便于发现,可标出“ ”号)生:下一行中间的各个数分别等于它“肩上”的两数之和.(如:1+2=3)师:(2)说出每项中字母和的次数排列规律.生:展开式中每项字母的次数从高到低排列,字母的次数从低到高排列.师:(3)展开式中的项数与乘方指数有何关系?生:展开式中的项数比乘方指数多1.师:你能按上述规律写出的展开式吗?生:.(学生同桌校对,一位学生板演.)【设计意图:教师用边讲边问的形式,通过让学生自己总结、发现规律,挖掘学习材料潜在的意义,从而使学习成为有意义的学习. 】师:将上述各展开式的每项系数再整理成如下模型: 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1师:对上表你还有什么规律可发现?生1:最外侧的系数都是1.生2:展开式中第二项的系数都等于乘方指数.生3:展开式中各项的次数等于都乘方指数.生4:系数成左、右对称排列……【设计意图:虽然,教师将此“三角形”模型以定论的形式呈现给学生,但是,它毕竟不是最后的结果,而是一种寻找系数规律的有效工具,便于学生将新的学习材料同自己原有的认知结构联系起来,并纳入到原有认知结构中而出现意义.这样的学习是有意义的而不是机械的,是主动建构的而不是被动死记的心理过程. 】四、范例讲解,应用新知师:例1 若今天是星期一,再过天后是星期几?怎么算?生1:星期二,将问题转化为求“后的余数”是1.生2:(此方法学生若未提及,教师给予讲解).师:(例1延伸)若今天是星期一,再过天后是星期几?怎么算?生1:猜想星期二,然后从.生2:求,前四项的和是7的倍数,所以除以7的余数是1,所以再过天后是星期二.师:(例1拓展)若今天是星期一,再过天后是星期几?生:的展开式中前项都含有7,所以除以7的余数是1,所以再过天后是星期二.【设计意图:从简单到复杂,从特殊到一般,层层推进,既深化新知,又激化学生的思维,更激化学生从认知结构中已有的知识和经验,便于学生类比学习. 】 五、纵横斜探,深度挖掘师:发给每位学生一张Excel表格.(表格上可先填好第一、二、三行的数字) A列B列C列D列E列F列G列H列I列J列K列求和第0行11第1行11 2第2行121 4第3行1331 8第4行14641 16第5行15101051 32第6行1615201561 64第7行172135352171 128第8行18285670562881 256第9行193684126126843691 512第10行11045120210252210120451011024… 生:四人一小组共同制作完成Excel表格《杨辉三角.xls ( 杨辉三角.xls )》.师:你能找到各行数字之和的规律吗?并用字母表示第行之和的结果.生:从求和的结果规律看,第行之和的结果为.师:观察和它的展开式,你能验证此规律成立的理由吗?生:当时,左边=,而右边等于展开式中每项系数相加(因为1的任何正整数次幂都是1).师:若学生想不到此验证思路,教师可借助当时,,即.这种验证方法叫数学中的赋值法.师:我们再从右斜线上算各行数字之和,有什么规律? A列B列C列D列E列F列G列第0行1第1行11 第2行121 第3行1331 第4行14641 第5行15101051 第6行1615201561第7行17213535217生:1,1,2,3,5,8,13,21,…. 从第三个数起,每一个数都等于它前面两个数的和.师:这就是著名的斐波那契数列.【设计意图:培养学生观察探究能力,再发现杨辉三角蕴涵了许多优美的规律,让学生充分展开思维进入研究状态,形成爱数学的好习惯. 】六、走入[斐波那契数列] 中世纪意大利数学家斐波那契的传世之作《算术之法》中提出了一个饶有趣味的问题:假定一对刚出生的兔子一个月就能长成大兔子,再过一个月就开始生下一对小兔子,并且以后每个月都生一对小兔子.设所生一对兔子均为一雄一雌,且均无死亡.问一对刚出生的小兔一年内可以繁殖成多少对兔子?兔子繁殖问题可以从杨辉三角得到答案:右侧从上而下的一列数1,1,2,3,5,8,13,…,正好是刚生的兔子对数,第一个月后的兔子对数.第二个月后的兔子对数,第三个月后的兔子对数,…n个月后的兔子的对数.“兔子繁殖问题”的答案233.【设计意图:通过体验斐波那契数列,呈现数学的趣味性,提高课堂学习氛围,达到学以致用的目的. 】
亮点与反思:这是一堂生动有效的综合实践活动课!在这课堂中,一通过学生实验操作、合作学习,引导学生观察、讨论,联想已有知识经验(面积验证、多项式乘法)分析新的问题(求),和探究杨辉三角规律及应用等活动,让学生亲历知识发生过程,从中感悟和获取数学知识、方法和思想,从而达成多方位提高学生数学素养.二教师的角色转变了,不再是传统教学中的“教教材”,而是主动寻找教材中的数学知识与学生已有知识有机联系为切入点,以学生所具备丰富信息出发,灵活展开教学,使枯燥的数学问题变为活生生的探究,增强了学生对数学内容的亲切感,使学生学得主动、学得开心,真正成为学习的主人.新课程的教学更需要教师注重创造性地使用教材,挖掘和盘活数学文本;要根据学生心理、学习需求、知识层面钻研教材,确定“以学定教”, 预设课堂,彰显丰盈的数学课.
8. 板书设计
杨辉三角和两数和的乘方
亮点与反思:这个板书设计并不突显创意,而是较完整地展现了课堂教学的主要内容,是常规而实用的板书设计。
9. 作业设计:
(1)通过网络搜索有关杨辉三角资料,进行再阅读,领悟其精髓.(2)结合资料,进行再探索.(有能力的学生写一篇数学小论文)
亮点与反思:作业是课堂的延伸,这两项作业,既开放又颇有点读后感的样式,是对学生课堂所学的知识再体验、再深化,同时又注重学生分层次性和可持续发展性.
10. 问题研讨:提出2-3个与本课设计相关的、值得反思和讨论的问题。(1)在平时教学中,对阅读材料使用常流于形式:如作导入新课的素材(显得肤浅);课堂中插入介绍(感觉生硬);布置学生课外阅读(难以落实).如何开发、有效地使用阅读材料,更好地发挥它在教材、教学中的作用?(2)探究式教学中教师主导地位和学生主体地位在尺度上把握,和何时收何放在时机上选择感到有些困难.
1张
1张
2张
(如图1)
(如图2)
3个
3个
1个
1个
(如图4)
(如图3)
学生板演
范例讲解
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《杨辉三角和两数和的乘方》综合实践活动课一、合作学习,形成技能师:请同学们准备好2张正方形、2张长方形的纸片(如图1).将它们拼成一个大正方形,并运用面积之间的关系,验证完全平方式. 生:动手操作完成(如图2),写出验证完全平方式.师:归纳面积验证的思路,大整块面积=所有小块面积之和.师:请同学们准备好2个立方体、8个长方体的纸盒(如图3).将它们搭成一个棱长为的立方体,并运用体积之间的关系,写出一条恒等式.生:四人小组合作,动手操作完成(如图4),写出一条恒等式.生:.(要求按的次数从高到低排列)【设计意图:通过学生的实验操作,得出恒等式,注重了知识的建构,体验了从平面到立体的空间思维,渗透了数形结合的数学思想. 】师:我们已经得到了和展开公式,试想生:学生先独立完成,然后同桌讨论交流. 生1:生2:师:我们也知道下面将计算结果中各展开式的每项系数排列成下表(简称系数表): 1 1 1 2 1 1 3 3 1 1 4 6 4 1师:因上表形如三角形,我国古代数学家杨辉对其有过深入研究,所以称它为杨辉三角,并提出课题.【设计意图:通过合作学习,从不同角度训练学生的思维,既提高学生学习兴趣,又培养合作团队精神和创造能力. 】二、介绍杨辉,感受成就杨辉,杭州钱塘人。中国南宋末年数学家,数学教育家.著作甚多,他编著的数学书共五种二十一卷,著有《详解九章算法》十二卷(1261年)、《日用算法》二卷、《乘除通变本末》三卷、《田亩比类乘除算法》二卷、《续古摘奇算法》二卷.其中后三种合称《杨辉算法》,朝鲜、日本等国均有译本出版,流传世界.
“杨辉三角”出现在杨辉编著的《详解九章算法》一书中,该书还说明此表源于我国北宋数学家贾宪(约公元11世纪)的“开方作法本源图”,这表明我国发现这个表不晚于11世纪.因此,我们把此表叫杨辉三角或贾宪三角.在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的(Blaise Pascal, 1623年~1662年),他们把这个表叫做帕斯卡三角.这就是说,杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.【设计意图:了解数学家杨辉及其成就, 增强民族自豪感;让学生体会到研究杨辉三角就是体察杨辉的探索精神,以鼓励学生探究的热情. 】三、探求规律,形成新知1 1 1 2 1 1 3 3 1 1 4 6 4 1 师:(1)请你找出上述数据上下行之间的规律.(便于发现,可标出“ ”号)生:下一行中间的各个数分别等于它“肩上”的两数之和.(如:1+2=3)师:(2)说出每项中字母和的次数排列规律.生:展开式中每项字母的次数从高到低排列,字母的次数从低到高排列.师:(3)展开式中的项数与乘方指数有何关系?生:展开式中的项数比乘方指数多1.师:你能按上述规律写出的展开式吗?生:.(学生同桌校对,一位学生板演.)【设计意图:教师用边讲边问的形式,通过让学生自己总结、发现规律,挖掘学习材料潜在的意义,从而使学习成为有意义的学习. 】师:将上述各展开式的每项系数再整理成如下模型: 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1师:对上表你还有什么规律可发现?生1:最外侧的系数都是1.生2:展开式中第二项的系数都等于乘方指数.生3:展开式中各项的次数等于都乘方指数.生4:系数成左、右对称排列……【设计意图:虽然,教师将此“三角形”模型以定论的形式呈现给学生,但是,它毕竟不是最后的结果,而是一种寻找系数规律的有效工具,便于学生将新的学习材料同自己原有的认知结构联系起来,并纳入到原有认知结构中而出现意义.这样的学习是有意义的而不是机械的,是主动建构的而不是被动死记的心理过程. 】四、范例讲解,应用新知师:例1 若今天是星期一,再过天后是星期几?怎么算?生1:星期二,将问题转化为求“后的余数”是1.生2:(此方法学生若未提及,教师给予讲解).师:(例1延伸)若今天是星期一,再过天后是星期几?怎么算?生1:猜想星期二,然后从.生2:求,前四项的和是7的倍数,所以除以7的余数是1,所以再过天后是星期二.师:(例1拓展)若今天是星期一,再过天后是星期几?生:的展开式中前项都含有7,所以除以7的余数是1,所以再过天后是星期二.【设计意图:从简单到复杂,从特殊到一般,层层推进,既深化新知,又激化学生的思维,更激化学生从认知结构中已有的知识和经验,便于学生类比学习. 】 五、纵横斜探,深度挖掘师:发给每位学生一张Excel表格.(表格上可先填好第一、二、三行的数字) A列B列C列D列E列F列G列H列I列J列K列求和第0行11第1行11 2第2行121 4第3行1331 8第4行14641 16第5行15101051 32第6行1615201561 64第7行172135352171 128第8行18285670562881 256第9行193684126126843691 512第10行11045120210252210120451011024… 生:四人一小组共同制作完成Excel表格《杨辉三角.xls ( 杨辉三角.xls )》.师:你能找到各行数字之和的规律吗?并用字母表示第行之和的结果.生:从求和的结果规律看,第行之和的结果为.师:观察和它的展开式,你能验证此规律成立的理由吗?生:当时,左边=,而右边等于展开式中每项系数相加(因为1的任何正整数次幂都是1).师:若学生想不到此验证思路,教师可借助当时,,即.这种验证方法叫数学中的赋值法.师:我们再从右斜线上算各行数字之和,有什么规律? A列B列C列D列E列F列G列第0行1第1行11 第2行121 第3行1331 第4行14641 第5行15101051 第6行1615201561第7行17213535217生:1,1,2,3,5,8,13,21,…. 从第三个数起,每一个数都等于它前面两个数的和.师:这就是著名的斐波那契数列.【设计意图:培养学生观察探究能力,再发现杨辉三角蕴涵了许多优美的规律,让学生充分展开思维进入研究状态,形成爱数学的好习惯. 】六、走入[斐波那契数列] 中世纪意大利数学家斐波那契的传世之作《算术之法》中提出了一个饶有趣味的问题:假定一对刚出生的兔子一个月就能长成大兔子,再过一个月就开始生下一对小兔子,并且以后每个月都生一对小兔子.设所生一对兔子均为一雄一雌,且均无死亡.问一对刚出生的小兔一年内可以繁殖成多少对兔子?兔子繁殖问题可以从杨辉三角得到答案:右侧从上而下的一列数1,1,2,3,5,8,13,…,正好是刚生的兔子对数,第一个月后的兔子对数.第二个月后的兔子对数,第三个月后的兔子对数,…n个月后的兔子的对数.“兔子繁殖问题”的答案233.【设计意图:通过体验斐波那契数列,呈现数学的趣味性,提高课堂学习氛围,达到学以致用的目的. 】
亮点与反思:这是一堂生动有效的综合实践活动课!在这课堂中,一通过学生实验操作、合作学习,引导学生观察、讨论,联想已有知识经验(面积验证、多项式乘法)分析新的问题(求),和探究杨辉三角规律及应用等活动,让学生亲历知识发生过程,从中感悟和获取数学知识、方法和思想,从而达成多方位提高学生数学素养.二教师的角色转变了,不再是传统教学中的“教教材”,而是主动寻找教材中的数学知识与学生已有知识有机联系为切入点,以学生所具备丰富信息出发,灵活展开教学,使枯燥的数学问题变为活生生的探究,增强了学生对数学内容的亲切感,使学生学得主动、学得开心,真正成为学习的主人.新课程的教学更需要教师注重创造性地使用教材,挖掘和盘活数学文本;要根据学生心理、学习需求、知识层面钻研教材,确定“以学定教”, 预设课堂,彰显丰盈的数学课.
8. 板书设计
杨辉三角和两数和的乘方
亮点与反思:这个板书设计并不突显创意,而是较完整地展现了课堂教学的主要内容,是常规而实用的板书设计。
9. 作业设计:
(1)通过网络搜索有关杨辉三角资料,进行再阅读,领悟其精髓.(2)结合资料,进行再探索.(有能力的学生写一篇数学小论文)
亮点与反思:作业是课堂的延伸,这两项作业,既开放又颇有点读后感的样式,是对学生课堂所学的知识再体验、再深化,同时又注重学生分层次性和可持续发展性.
10. 问题研讨:提出2-3个与本课设计相关的、值得反思和讨论的问题。(1)在平时教学中,对阅读材料使用常流于形式:如作导入新课的素材(显得肤浅);课堂中插入介绍(感觉生硬);布置学生课外阅读(难以落实).如何开发、有效地使用阅读材料,更好地发挥它在教材、教学中的作用?(2)探究式教学中教师主导地位和学生主体地位在尺度上把握,和何时收何放在时机上选择感到有些困难.
1张
1张
2张
(如图1)
(如图2)
3个
3个
1个
1个
(如图4)
(如图3)
学生板演
范例讲解
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
