5.6同底数幂的除法（2）

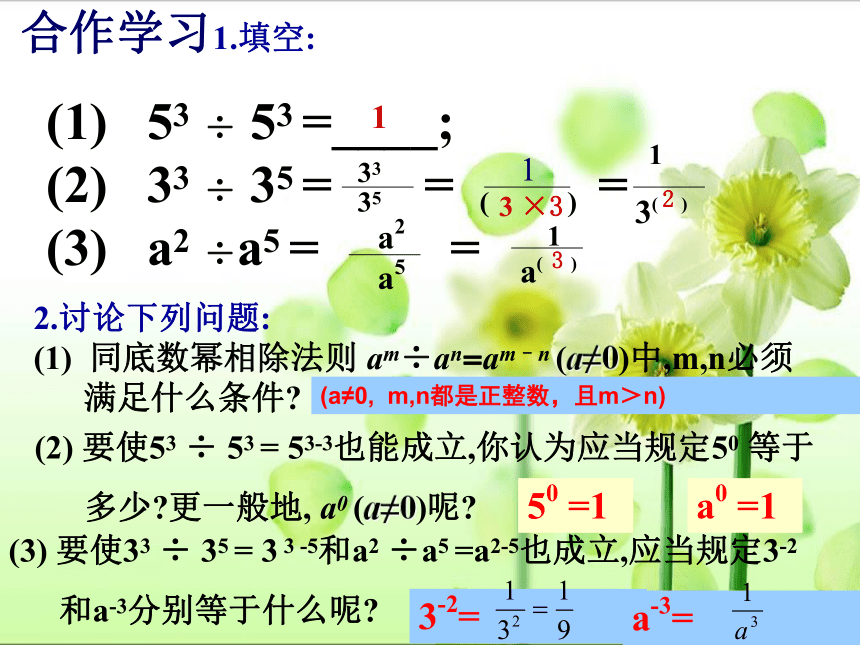
课件16张PPT。5.6同底数幂的除法(2) (1) 53 ÷ 53 =____;
(2) 33 ÷ 35 = = =
(3) a2 ÷a5 = = 合作学习1.填空: 35 33( )13( )1a( )13 ×3232.讨论下列问题:
(1) 同底数幂相除法则 am÷an=am–n (a≠0)中,m,n必须
满足什么条件?(2) 要使53 ÷ 53 = 53-3也能成立,你认为应当规定50 等于
多少?更一般地, a0 (a≠0)呢?(3) 要使33 ÷ 35 = 3 3 -5和a2 ÷a5 =a2-5也成立,应当规定3-2
和a-3分别等于什么呢?
1a2a550 =1(a≠0, m,n都是正整数，且m＞n)a0 =13-2=a-3=我们规定：任何不等于零的数的零次幂都等于1我们规定：任何不等于零的数的-p(p 是正整数)次幂,等于
这个数的p次幂的倒数. 指数从正整数推广到了整数，正整数指数幂的各种运算法则对整数指数幂都适用。 第一关：法官审判（1）下列计算对吗？为什么？ 错的请改正。
①（－3）0=－1
②（－2）－1 ＝1
③ 2－2=－4
④a3÷a3=0
⑤ ap·a－p =1 （a≠0） 例1. 用分数或整数表示下列各负整数指数幂的值(1) 10-3 (2) (-0.5)-3 (3) (-3)-4 第二关：学以致用(4) 第三关：牛刀小试1、用分数或整数表示下列各负整数指数幂的值(1) 100-2 (2) (-1)-3 (3) (-0.1)-2(6) (4) （-71）-1 (5) 0.1-3第四关：激流勇进（计算）(1) 950 ×(-5)-1 (2) 3.6× 10-3
(3) a3 ÷(-10)0 (4) (-3)5 ÷36 （5）第五关：快乐点击3.5 －10探究延伸，建立模型做一做：
将0.000 05输入计算器，再将它乘以0.000 007，观察你的计算器的显示，它表示什么数？显示为: 与你的同伴交流计算器是怎样表示绝对值较小的数。
这其实是一种用科学记数法来表示很小的数 1010.10.010.0010.0001 练一练1. 把下列各数表示成 a ×10n ( 1≤a< 10,n为整数)
的形式(1) 12000(2) 0.0021(3) 0.00005012、用小数表示下列各数：
①1.6×10－3
②－3.2×10－5拓展思维（1） 已知 2n=8,则4n-1=
(2) a10÷ an= a4 ，则n=
(3) 812-x=27x+4,则 x=
(4) x2-3x+1=0, 求x2+x-2的值归纳小结
知识点
① a0=1（a≠0）
② a－p= （a≠0，p是正整数）
③ 用科学记数法表示较小的数 再见