5.4乘法公式 （1）

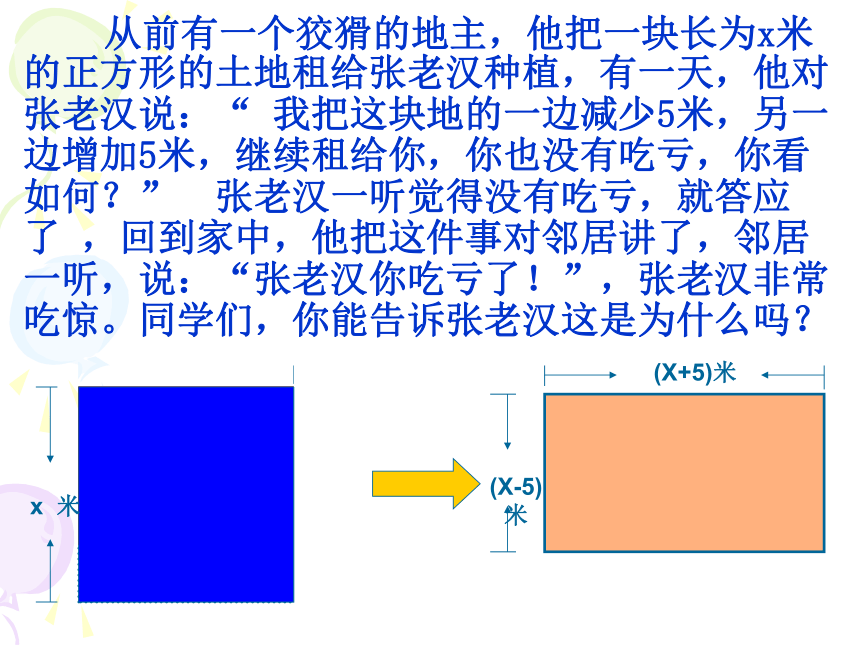
课件24张PPT。2019/3/95.4 乘法公式（1） 从前有一个狡猾的地主，他把一块长为x米的正方形的土地租给张老汉种植，有一天，他对张老汉说：“ 我把这块地的一边减少5米，另一边增加5米，继续租给你，你也没有吃亏，你看如何？” 张老汉一听觉得没有吃亏，就答应了 ，回到家中，他把这件事对邻居讲了，邻居一听，说：“张老汉你吃亏了！”，张老汉非常吃惊。同学们，你能告诉张老汉这是为什么吗？ (a+2) (a-2) =? (2) (3-x)(3+x) = ?
(3) (2m+n)(2m-n) = ?观察以上算式，你发现了什么规律？运算出结果，你又发现了什么？(a+b)(a-b)两数和与这两数差的积，
等于这两数的平方差。 平方差公式= a2-b2找出下列各题中的a,b项
　 1. (3m－1 )(3m＋1)
2. (－1+3n)(－1－3n)
3. (－2b－5)(2b－5) 考考你的 眼力 1．口答下列各题：
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
??(4)(a-b)(-a-b)= _________a2-b2a2-b2b2-a2b2-a2(1) (a+b)(?a?b) ；
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) 2.下列式子可用平方差公式计算吗? 为什么? 如果能够，怎样计算? (不能) (不能) (能) 解:原式＝?(a2 ?b2) ＝b2?a2 (不能) 问题：利用平方差公式计算的关键是__________
怎样确定a与b______________________（一）应用公式：
例1. 利用平方差公式计算（先确定各题的a与b，再填空）
(1)(5+6x)(5-6x)=( )2-( )2=______
(2)(x-2y)(x+2y)=( )2-( )2=_______
(3)(-m+n)(-m-n)=( )2-( )2=_______
准确确定a和b符号相同的项是a,符号相反的项是b56x25-36x2x2yx2-4y2-mnm2-n2例题精讲一例1.运用平方差公式进行计算:1.计算（口答）：
（1）（x+1)(x-1)
(2) (x+2)(x-2)
(3) (m+n)(m-n)
(4) (m+6)(m-6)
(5) (x+2y)(x-2y)
(6) (3x-2)(3x+2)
(7) (b+5a)(b-5a) = x2-1= m2-n2= x2-(2y)2 = x2-4y2= m2 - 6 2 = m2-36= (3x)2-22 = 9x2-4= x2 - 4= b2- (5a)2 =b2-25a2判断并改错：
(1) (a+3)(a-3)=a2-3 ( )
改正：
(2)(5y+2)(5y-2)=5y2-4 ( )
改正：
(3) (1- 4xy)(-1- 4xy)=1-16x2y2 ( )
改正：
(4)(-ab+3c)(-3c-ab)=a2b2-9c2 ( )
改正：
(5) (-m+7)(7-m)=m2-49 ( )
改正：××××√(a+3)(a-3)=a2-9(5y+2)(5y-2)=25y2-4原式=(- 4xy+1)(- 4xy-1)=16x2y2-1(-m+7)(7-m)=(7-m)(7-m)=(7-m)2练一练(1)运用平方差公式进行计算:
(1)(x+m)(x-m) (2)(3a+b)(3a-b)
(3)(5a-4b)(5a+4b) (4)(-5x-3y)(-5x+3y)
王敏捷同学去商店买了单价是9.8元/千克的糖果10.2千克，
售货员刚拿起计算器，王敏捷就说出应99.96元，结果与售货员计算出的结果相吻合。
售货员很惊讶地说：“你好象是个神童，怎么算得这么快？”
王敏捷同学说：“过奖了，我利用了在数学上刚学过的一个公式。”
你知道王敏捷同学用的是一个什么样的公式吗？怎么计算的吗?例题精讲二例2.利用平方差公式计算:
103×97
59.8×60.2 练一练(2)运用平方差公式进行计算:(1)(4)(6)(5)(2)(3)挑战自我,每个图片背后都有一道题目,选择你喜欢的运动.小 结 (a+b)(a-b)=a2- b2两数和与这两数差的积，等于它们的平方差注意1)左边为两个数的和与差的积,右边为两个数的平方差
2)有些式子通过适当变形实质上能用公式
3)公式中的a和b可以是数,也可以是整式
4)最后结果必须化简再见　已知(N+56)2=1234567,
求(N+46)(N+66)的值运用平方差公式计算:5678×5680-56792=(5679-1)(5679+1)-56792=56792 -1 -56792= -1 利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216如果A=1234567892, B=123456788×123456790,
试比较A与B的大小.