5.1 同底数幂的乘法(1)

课件22张PPT。5.1 同底数幂的乘法光的速度大约是3×105 千米/秒，若1年以3×107秒计算，那么光在1年可通过多少距离？　　最近发现太阳系之外的第100颗行星距离地球有100光年，求此行星与地球之间的距离？关注生活列式为：
102×3×105×3×107
＝9×102×105×107
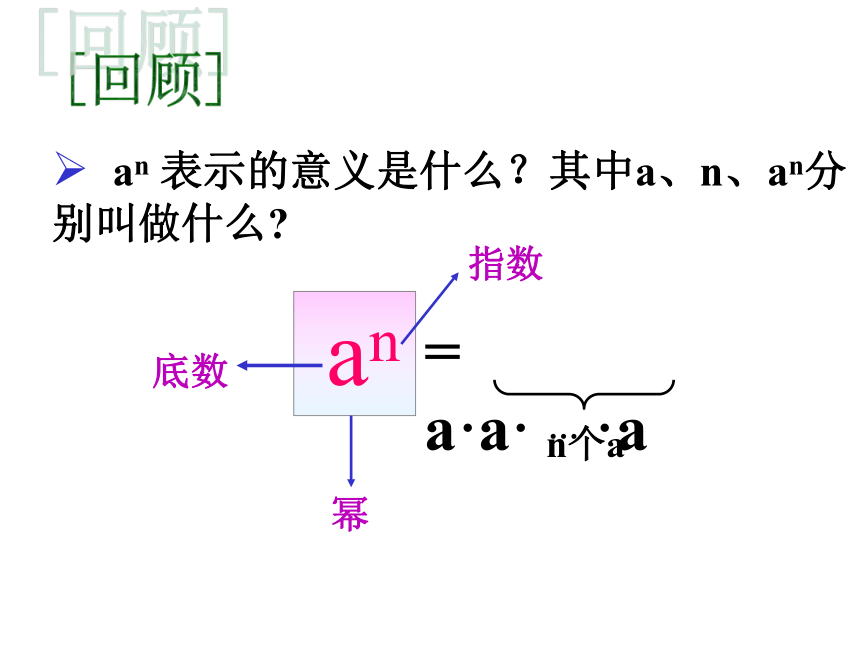
那么：102×105×107等于多少呢？ an 表示的意义是什么？其中a、n、an分 别叫做什么? an底数幂指数[回顾]合作学习 23×22 = ( 　　　　 ) ×( 　　 )
=________________　　
　　　　　　=2( ) =2( )+( )2 × 2 × 22 × 22 × 2 × 2 × 2 × 2532
　　(2) 102 × 105
= ( ) × ( )
=_________
=10( ) = 10( )+( )10×1010×10×10×10×1010×10×10×10×10×10×107２５合作学习(3) a4· a3
= ( ) · ( )
= _________
=a( ) = a( )+( )

a·a·aa·a·a·a·a·a·a743a ·a ·a ·a 猜想:当底数是字母时,是否也有同底数幂相乘,底数不变,指数相加呢
(m+n)个am个an个a同底数幂的乘法法则:底数 指数 .不变相加同底数幂相乘,（m、n都是正整数）例1 计算下列各式,结果用幂的形式表示 (1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3 (3) x3 · x5 (4) (a-b)2 (a-b)做一做 当三个或三个以上同底数幂相乘时，
是否也具有这一性质呢？ 怎样用公式
表示？想一想：am · an · ap 等于什么？开头问题中第100颗行星与地球之间的距离约为 千米。9×102×105 × 107 9 ×1014=9×102+5+7=9 ×1014（千米）请帮忙出出主意：
当底数出现互为相反数时，该怎么办呢？
下面的计算对不对？如果不对，怎样改正？
（1）b5 · b5= 2b5 （ ） （2）b5 + b5 = b10 （ ）
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x2 · x3 = x5 (-2)8 · 23 = 211 a · a6 = a7× × × ×××? 判一判 ? （3）x2 ·x3 = x6 ( ) （4）(-2)8 · 2 3 = (-2)11 ( )（5）a · a6 = a6 ( ) （6）m + m3 = m4 ( ) 例2　我国自行研制的“神威 I”计算机的峰值运算速度达到每秒 3840亿次.如果按这个速度工作一整天,那么它能运算多少次? (结果保留3个有效数字)解: 3840亿次=3.84× 103× 108次,24时=24× 3.6× 103秒。( 3.84× 103× 108 ) × (24× 3.6× 103)= (3.84 ×24 ×3.6) × (103 ×108 ×103)= 331.776 ×1014答:它一天约能运算3.32× 1016次。闯关第一关第二关第三关第四关 填空：
（1）x5 .（ ）=　x 2008
（2）x4· x3= 27 求Ｘ的值
X2003闯关第一关X= 22. 计算：
a2?a3 + a?a4第二关3.如果an-2?an+1=a11,
则n= .6第三关
4．已知：am=2，an=3.

　求am+n . 第四关小结通过这节课的学习,你有什么收获?再见作业：作业本5.1(1)
　　　课本作业题??套餐一：看谁计算又对又快（结果用幂的形式表示）　　３４ 　１０10 －３５ b8 （2） １０５ ·１０５（3）（－３）２ ·（－３）３ （4） b5 · b２ · b （1） ３×３３快乐套餐　　套餐二： 判断（正确的 打“√”，错误的打“×”） x4·x5=x20 ( ) (2) x·x3=x3 ( )
(3) x4+x5=x9 ( ) (3)x2·x2=2x4 ( )
(5)(-x)2 · (-x)3 = (-x)5= -x5 ( )
(6)a3·a2 - a2·a3 = 0 ( )
(7)a3·b5=(ab)8 ( ) (8) y7+y7=y14 ( )
√√××××××　套餐三：填空：
（1）x6 ·（ ）=　x 9 （2）a ·（ ）=　a6
（3）x · x3（ ）= x7 （4）xm ·（　 ）＝ｘ3m
变式训练x3a5 x3ｘ2m？？？（5） 8× 4 = 2x，则 x = ；
×2322 =2552x= 25