浙教新版七年级下第六章数据与统计图表练习
文档属性
| 名称 | 浙教新版七年级下第六章数据与统计图表练习 |  | |
| 格式 | zip | ||
| 文件大小 | 655.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-01-19 16:54:43 | ||
图片预览


文档简介
浙教新版七年级下第六章数据与统计图表练习
姓名:__________班级:__________考号:__________
一 、选择题(本大题共10小题)
1.为了解某市参加中考的32000名学生的体重情况,抽查了其中1500名学生的体重进行统计分析,下列叙述正确的是( )21世纪教育网版权所有
A.32000名学生是总体 B.每名学生是总体的一个个体
C.1500名学生的体重是总体的一个样本 D.以上调查是普查
2.下列调査中,适合采用全面调査(普査)方式的是()
A.对綦江河水质情况的调査 B.对端午节期间市场上粽子质量情况的调査
C.对某班50名同学体重情况的调査 D.对某类烟花爆竹燃放安全情况的调査
3.黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%,请估计黄石地区1000斤蚕豆种子中不能发芽的大约有( )21cnjy.com
A.971斤 B.129斤 C.97.1斤 D.29斤
4.如图是某国产品牌手机专卖店今年8﹣12月高清大屏手机销售额折线统计图.根据图中信息,可以判断相邻两个月高清大屏手机销售额变化最大的是( )
A. 8﹣9月 B. 9﹣10月 C. 10﹣11月 D. 11﹣12月
5.如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
A.2~4小时 B.4~6小时 C.6~8小时 D.8~10小时
6.某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
A.25人 B.35人 C.40人 D.100人
7.下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B.条形图 C.折线图 D.直方图
8.已知数据:10,8,6,10,8,13,11,10,12,7,9,8,12,9,11,12,9,10,11,10,那么频数为4的一组是( )www-2-1-cnjy-com
A.5.5~7.5 B.7.5~9.5 C.9.5~11.5 D.11.5~13.5
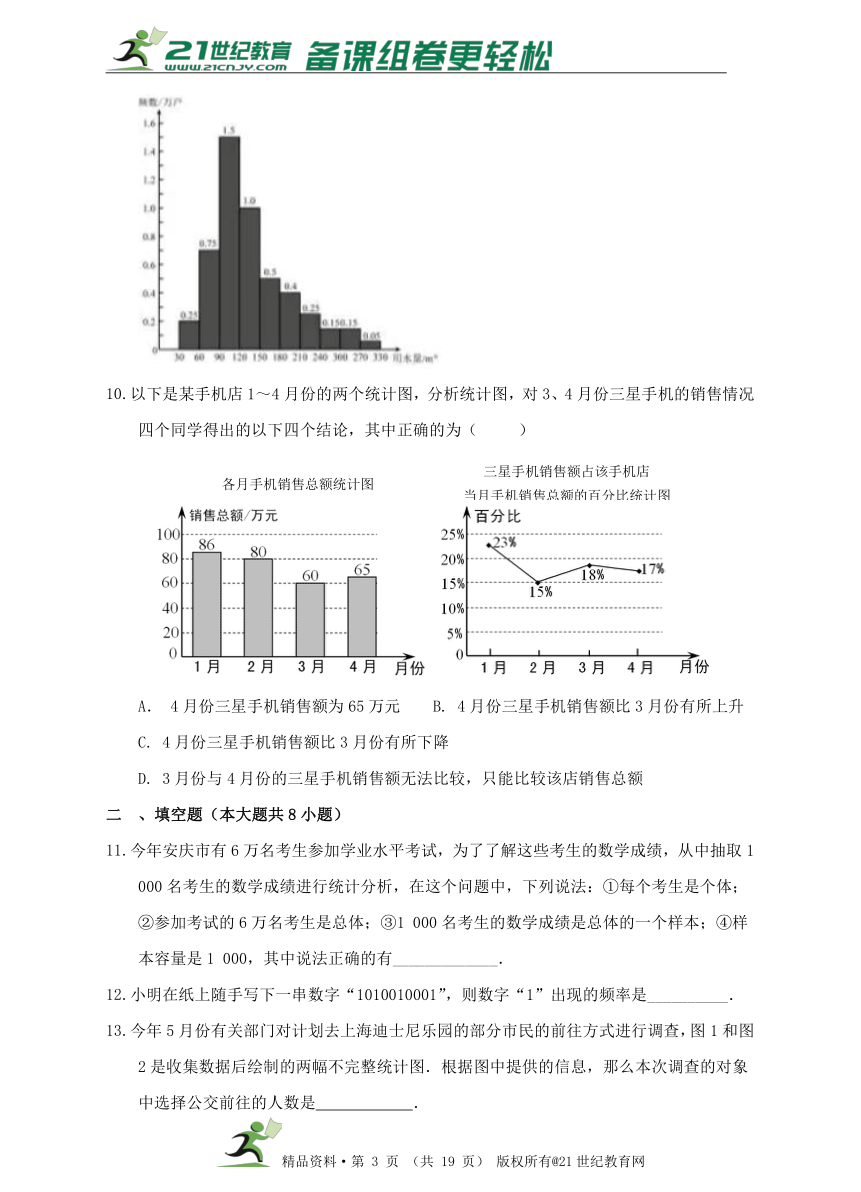
9.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增。计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%。为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:),绘制了统计图,如图所示,下面有四个推断正确的是( )www.21-cn-jy.com
① 年用水量不超过180的该市居民家庭按第一档水价交费
② 年用水量超过240的该市居民家庭按第三档水价交费
③ 该市居民家庭年用水量的中位数在150-180之间
④ 该市居民家庭年用水量的平均数不超过180
A. ①③ B. ①④ C.②③ D.②④
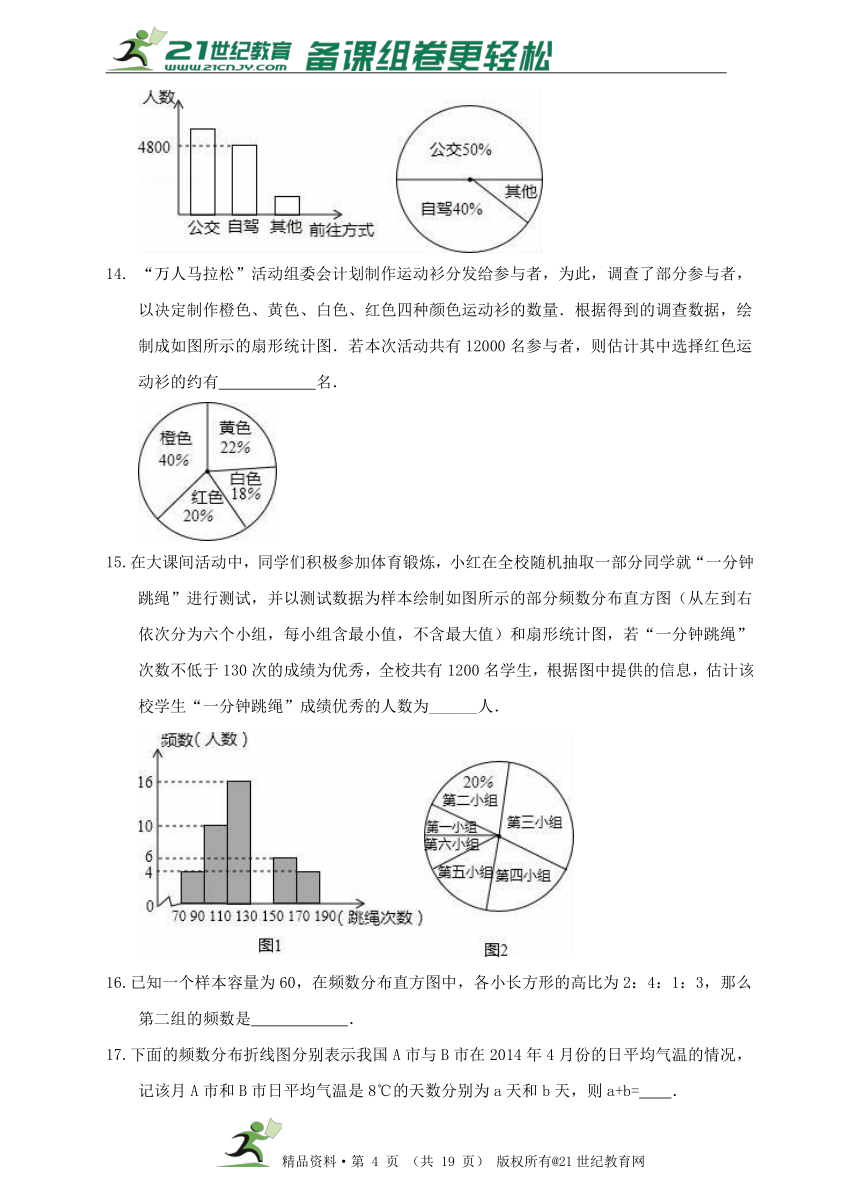
10.以下是某手机店1~4月份的两个统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
A. 4月份三星手机销售额为65万元 B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
二 、填空题(本大题共8小题)
11.今年安庆市有6万名考生参加学业水平考试,为了了解这些考生的数学成绩,从中抽取1 000名考生的数学成绩进行统计分析,在这个问题中,下列说法:①每个考生是个体;②参加考试的6万名考生是总体;③1 000名考生的数学成绩是总体的一个样本;④样本容量是1 000,其中说法正确的有_____________.【来源:21cnj*y.co*m】
12.小明在纸上随手写下一串数字“1010010001”,则数字“1”出现的频率是__________.
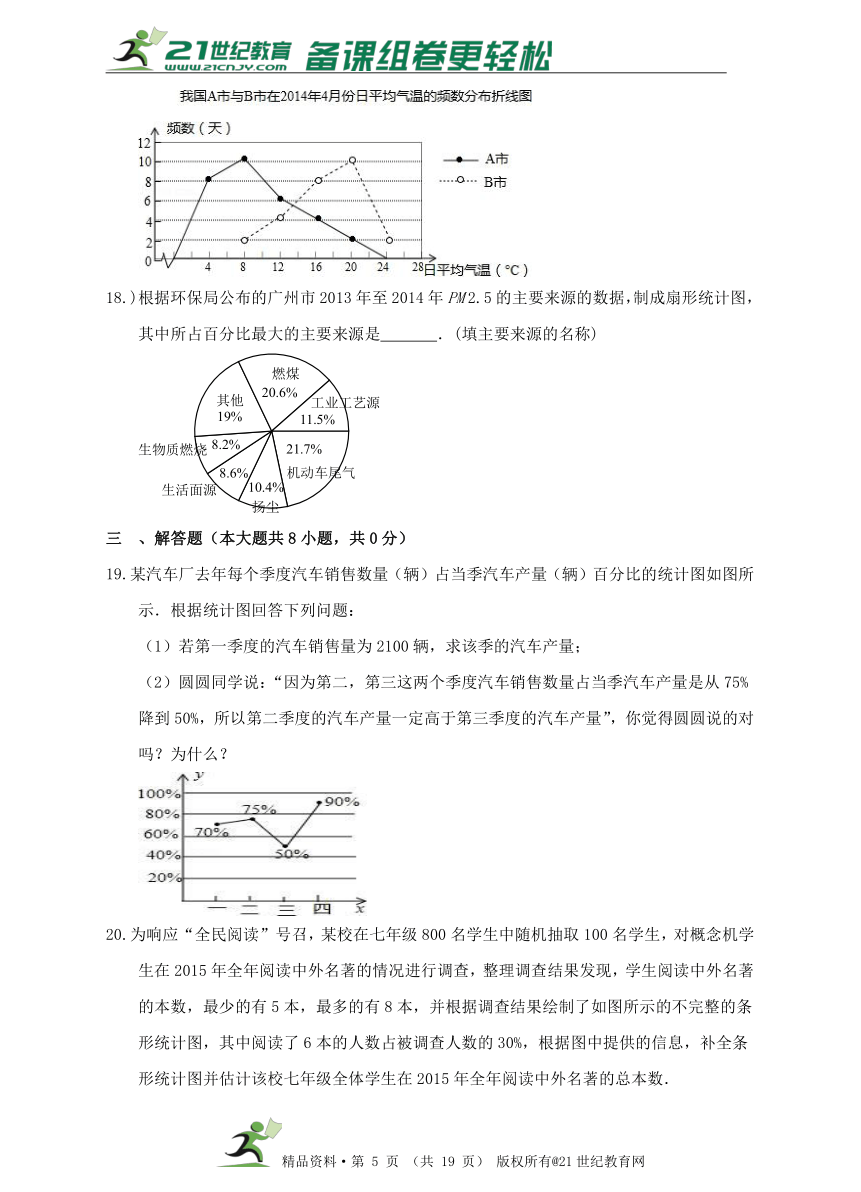
13.今年5月份有关部门对计划去上海迪士尼乐园的部分市民的前往方式进行调查,图1和图2是收集数据后绘制的两幅不完整统计图.根据图中提供的信息,那么本次调查的对象中选择公交前往的人数是 .
14. “万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有 名.21*cnjy*com
15.在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为______人.【版权所有:21教育】
16.已知一个样本容量为60,在频数分布直方图中,各小长方形的高比为2:4:1:3,那么第二组的频数是 .
17.下面的频数分布折线图分别表示我国A市与B市在2014年4月份的日平均气温的情况,记该月A市和B市日平均气温是8℃的天数分别为a天和b天,则a+b= .
18.)根据环保局公布的广州市2013年至2014年PM 2.5的主要来源的数据,制成扇形统计图,其中所占百分比最大的主要来源是 .(填主要来源的名称)
三 、解答题(本大题共8小题,共0分)
19.某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
20.为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对概念机学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.
21.某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人
(1)本次抽取的学生有 人;
(2)请补全扇形统计图;
(3)请估计该校1600名学生中对垃圾分类不了解的人数.
22.为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
23.为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
分组
频数
4.0≤x<4.2
2
4.2≤x<4.4
3
4.4≤x<4.6
5
4.6≤x<4.8
8
4.8≤x<5.0
17
5.0≤x<5.2
5
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
24.某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:21·世纪*教育网
(1)此次抽样调查的样本容量是______.
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?【出处:21教育名师】
25.绵阳七一中学开通了空中教育互联网在线学习平台,为了解学生使用情况,该校学生会把该平台使用情况分为A(经常使用)、B(偶尔使用)、C(不使用)三种类型,并设计了调查问卷、先后对该校初一(1)班和初一(2)班全体同学进行了问卷调查,并根据调查结果绘制成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)求此次被调查的学生总人数;
(2)求扇形统计图中代表类型C的扇形的圆心角,并补全折线统计图;
(3)若该校初一年级学生共有1000人,试根据此次调查结果估计该校初一年级中C类型学生约有多少人.
26.某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图;
(1)这次抽样调查的样本容量是 ,并补全条形图;
(2)D等级学生人数占被调查人数的百分比为 ,在扇形统计图中C等级所对应的圆心角为 °;【来源:21·世纪·教育·网】
(3)该校九年级学生有1500人,请你估计其中A等级的学生人数.
0.浙教新版七年级下第六章数据与统计图表练习答案解析
一 、选择题
1.分析:分别根据总体、个体、样本及调查的定义逐项判断即可.
解:
某市参加中考的32000名学生的体重情况是总体,故A错误;
每名学生的体重情况是总体的一个个体,故B错误;
1500名学生的体重情况是一个样本,故C正确;
该调查属于抽样调查,故D错误;
故选C.
2.分析: 由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.21·cn·jy·com
解:A,对綦江河水质情况的调査的调查应用抽样调查,大概知道水质情况就可以了,故此选项错误,
B,对端午节期间市场粽子质量的调查适用抽样调查,利用全面调查,就不能买了,故此选项错误;
C,对某班50名同学体重情况的调査适用全面调查,人数不多,全面调查准确,故此选项正确;
D,对某类烟花爆竹燃放安全情况的调査适用抽样调查,利用全面调查,破坏性极大,就不能买了,故此选项错误.21教育网
故选C.
3.分析:根据蚕豆种子的发芽率为97.1%,可以估计黄石地区1000斤蚕豆种子中不能发芽的大约有多少,本题得以解决.2-1-c-n-j-y
解:由题意可得,
黄石地区1000斤蚕豆种子中不能发芽的大约有:1000×(1﹣97.1%)=1000×0.029=29斤,21教育名师原创作品
故选D.
.
4.分析:根据折线图的数据,分别求出相邻两个月的高清大屏手机销售额的变化值,比较即可得解.
解:8﹣9月,30﹣23=7万元,
9﹣10月,30﹣25=5万元,
10﹣11月,25﹣15=10万元,
11﹣12月,19﹣15=4万元,
所以,相邻两个月中,高清大屏手机销售额变化最大的是10﹣11月.
故选C.
5.分析:根据条形统计图可以得到哪一组的人数最多,从而可以解答本题.
解:由条形统计图可得,
人数最多的一组是4~6小时,频数为22,
故选B.
6.分析:根据扇形统计图可得参加足球的人数最少,参加乒乓球的人数最多.
解:根据题意可得:总人数=25÷25%=100(人),则参加乒乓球的人数为:100×(1-35%-25%)=40(人).
故选C
7.分析:条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图比较清楚地反映出部分与部分、部分与整体之间的数量关系;据此进行解答即可.
解:在进行数据描述时,要显示部分在总体中所占的百分比,应采用扇形统计图; 故选:A.
8.分析:找出四组中的数字,判断出频数,即可做出判断.
解:5.5~7.5组有6,7,频数为2;7.5~9.5组有8,8,9,8,9,9,频数为6;9.5~11.5组有10,10,11,10,11,10,11,10,频数为8;11.5~13.5组有13,12,12,12,频数为4.
故选D.
9.解:年用水量不超过180的居民家庭有:0.25+0.75+1.5+1+0.5=4(万),=80%,
所以,①正确;
年用水量超过240的居民家庭有:0.15+0.15+0.05=0.35(万),=7%,故②不正确;
30-120的有2.5万人,120-330的有2.5万人,中位数应该是120,故③不正确;
由于中位数为120,用水量小于150的有3.5万人,所以该市居民家庭年用水量的平均数不超过180,④正确。
10.分析:根据销售额=总销售额×所占的百分比求出销售额,再根据有理数大小比较得出答案
解:三星手机的销售额=单月手机的总销售额×三星手机所占的百分比.根据统计图可得:三星手机三月份的销售额为:60×18%=10.8(万元),四月份三星手机的销售额为:65×17%=11.05(万元),则根据以上信息可得B是正确的.
二 、填空题
11.分析: 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解:①每个考生的数学成绩是个体,命题错误;
②参加考试的6万名考生的成绩是总体,命题错误;
③④正确.
故答案是:③④.
12.分析:首先计算数字的总数,以及1出现的频数,根据频率公式:频率=即可求解.
解:数字的总数是10,有4个1,
因而1出现的频率是:4÷10×100%=40%.
故答案是:40%.
13.分析:根据自驾车人数除以百分比,可得答案.
解:由题意,得
4800÷40%=12000,
公交12000×50%=6000,
故答案为:6000.
14.分析:根据样本中选择红色运动衫的人数占总数的百分比,据此可估计总体中选择红色运动衫的人数占总数的百分比近似相等,列式计算即可.21*cnjy*com
解:若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有12000×20%=2400(名),
故答案为:2400.
15.分析:首先由第二小组有10人,占20%,可求得总人数,再根据各小组频数之和等于数据总数求得第四小组的人数,利用总人数260乘以样本中“一分钟跳绳”成绩为优秀的人数所占的比例即可求解.
解:总人数是:10÷20%=50(人),
第四小组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,
所以该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×1200=480,
故答案为:480.
16.分析:根据各小长方形的高比为2:4:1:3,得频数之比为2:4:1:3,由此即可解决问题.
解:∵样本容量为60,各小长方形的高比为2:4:1:3,
∴那么第二组的频数是60×=24,
故答案为24.
17.分析:根据折线图即可求得a、b的值,从而求得代数式的值.
解:根据图表可得:a=10,b=2, 则a+b=10+2=12. 故答案为:12.
18.分析:根据扇形统计图可得:机动车尾气所占的百分比最大,则主要来源就是机动车尾气.
解:用一个圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分在总体中所占百分比的大小,这样的统计图叫做扇形统计图.所以一看数据就知道是机动车尾气
三 、解答题
19.分析:(1)根据每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图,可以求得第一季度的汽车销售量为2100辆时,该季的汽车产量;
(2)首先判断圆圆的说法错误,然后说明原因即可解答本题.
解:(1)由题意可得,
2100÷70%=3000(辆),
即该季的汽车产量是3000辆;
(2)圆圆的说法不对,
因为百分比仅能够表示所要考查的数据在总量中所占的比例,并不能反映总量的大小.
20.分析:由阅读了6本的人数占被调查人数的30%可求得阅读6本的人数,将总人数减去阅读数是5、6、8本的人数可得阅读7本人数,据此补全条形图可得;根据样本计算出平均每人的阅读量,再用平均数乘以七年级学生总数即可得答案.
解:根据题意,阅读了6本的人数为100×30%=30(人),
阅读了7本的人数为:100﹣20﹣30﹣﹣15=35(人),
补全条形图如图:
∵平均每位学生的阅读数量为: =6.45(本),
∴估计该校七年级全体学生在2015年全年阅读中外名著的总本数为800×6.45=5160本,
答:估计该校七年级全体学生在2015年全年阅读中外名著的总本数约为5160本.
21.分析:(1)根据不了解的人数除以不了解的人数所占的百分比,可得的答案;
(2)根据有理数的减法,可得答案;
(3)根据样本估计总体,可得答案.
解:(1)30÷10%=300,
故答案为:300;
(2)如图,
了解很少的人数所占的百分比1﹣30%﹣10%﹣20%=40%,
故答案为:40%,
(3)1600×30%=480人,
该校1600名学生中对垃圾分类不了解的人数480人.
22.分析:(1)根据条形统计图和扇形统计图可知选择劳技的学生60人,占总体的30%,从而可以求得调查学生人数;
(2)根据文学的百分比和(1)中求得的学生调查数可以求得文学的有多少人,从而可以求得体育的多少人,进而可以将条形统计图补充完整;
(3)根据调查的选择体育的学生所占的百分比可以估算出全校选择体育类的学生人数.
解:(1)60÷30%=200(人),
即本次被调查的学生有200人;
(2)选择文学的学生有:200×15%=30(人),
选择体育的学生有:200﹣24﹣60﹣30﹣16=70(人),
补全的条形统计图如下图所示,
(3)1600×(人).
即全校选择体育类的学生有560人.
23.分析:(1)求出频数之和即可.
(2)根据合格率=×100%即可解决问题.
(3)从两个不同的角度分析即可,答案不唯一.
解:(1)∵频数之和=40,
∴所抽取的学生人数40人.
(2)活动前该校学生的视力达标率==37.5%.
(3)①视力4.2≤x<4.4之间活动前有6人,活动后只有3人,人数明显减少.
②活动前合格率37.5%,活动后合格率55%,
视力保健活动的效果比较好.
24.分析:(1)根据10~15吨部分的用户数和百分比进行计算;(2)先根据频数分布直方图中的数据,求得“15吨~20吨”部分的用户数,再画图,最后根据该部分的用户数计算圆心角的度数;(3)根据用水25吨以内的用户数的占比,求得该地区6万用户中用水全部享受基本价格的户数.
解:(1)∵10÷10%=100(户)
∴样本容量是100;
(2)用水15~20吨的户数:100﹣10﹣36﹣24﹣8=22(户)
∴补充图如下:
“15吨~20吨”部分的圆心角的度数=360°×=79.2°
答:扇形图中“15吨~20吨”部分的圆心角的度数为79.2°.
(3)6×=4.08(万户)
答:该地区6万用户中约有4.08万户的用水全部享受基本价格.
25.分析:(1)先由折线统计图得到偶尔使用的学生有58人,再由扇形统计图得到了解很少的学生所占的百分比,然后用58除以这个百分比即可得到接受问卷调查的学生人数;
(2)先用总数分别减去其它三组的人数得到C的学生数,再补全折线统计图;用c部分所占的百分比乘以360°即可得到c部分所对应扇形的圆心角的大小;
(3)利用样本中c程度的百分比表示该校这两项所占的百分比,然后用1000乘以这个百分比即可得到c程度的总人数的估计值.2·1·c·n·j·y
解:(1)由扇形统计图知B类型人数所占比例为58%,从折线图知B类型总人数=26+32=58人,
所以此次被调查的学生总人数=58÷58%=100人;
(2)由折线图知A人数=18+14=32人,故A的比例为32÷100=32%,
所以C类比例=1﹣58%﹣32%=10%,
所以类型C的扇形的圆心角=360°×10%=36°,
C类人数=10%×100﹣2=8人,折线图如下:
(3)根据此次可得C的比例为10%,估计该校初一年级中C类型学生约1000×10%=100人.
26.分析:(1)由A等级的人数和其所占的百分比即可求出抽样调查的样本容量;求出B等级的人数即可全条形图;
(2)用B等级的人数除以总人数即可得到其占被调查人数的百分比;求出C等级所占的百分比,即可求出C等级所对应的圆心角;
(3)由扇形统计图可知A等级所占的百分比,进而可求出九年级学生其中A等级的学生人数.
解:(1)由条形统计图和扇形统计图可知总人数=16÷32%=50人,所以B等级的人数=50﹣16﹣10﹣4=20人,
故答案为:50;
补全条形图如图所示:
(2)D等级学生人数占被调查人数的百分比=×100%=8%;
在扇形统计图中C等级所对应的圆心角=8%×360°=28.8°,
故答案为:8%,28.8;
(3)该校九年级学生有1500人,估计其中A等级的学生人数=1500×32%=480人.
姓名:__________班级:__________考号:__________
一 、选择题(本大题共10小题)
1.为了解某市参加中考的32000名学生的体重情况,抽查了其中1500名学生的体重进行统计分析,下列叙述正确的是( )21世纪教育网版权所有
A.32000名学生是总体 B.每名学生是总体的一个个体
C.1500名学生的体重是总体的一个样本 D.以上调查是普查
2.下列调査中,适合采用全面调査(普査)方式的是()
A.对綦江河水质情况的调査 B.对端午节期间市场上粽子质量情况的调査
C.对某班50名同学体重情况的调査 D.对某类烟花爆竹燃放安全情况的调査
3.黄石农科所在相同条件下经试验发现蚕豆种子的发芽率为97.1%,请估计黄石地区1000斤蚕豆种子中不能发芽的大约有( )21cnjy.com
A.971斤 B.129斤 C.97.1斤 D.29斤
4.如图是某国产品牌手机专卖店今年8﹣12月高清大屏手机销售额折线统计图.根据图中信息,可以判断相邻两个月高清大屏手机销售额变化最大的是( )
A. 8﹣9月 B. 9﹣10月 C. 10﹣11月 D. 11﹣12月
5.如图是九(1)班45名同学每周课外阅读时间的频数直方图(每组含前一个边界值,不含后一个边界值).由图可知,人数最多的一组是( )
A.2~4小时 B.4~6小时 C.6~8小时 D.8~10小时
6.某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
A.25人 B.35人 C.40人 D.100人
7.下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形图 B.条形图 C.折线图 D.直方图
8.已知数据:10,8,6,10,8,13,11,10,12,7,9,8,12,9,11,12,9,10,11,10,那么频数为4的一组是( )www-2-1-cnjy-com
A.5.5~7.5 B.7.5~9.5 C.9.5~11.5 D.11.5~13.5
9.为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价,水价分档递增。计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%。为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:),绘制了统计图,如图所示,下面有四个推断正确的是( )www.21-cn-jy.com
① 年用水量不超过180的该市居民家庭按第一档水价交费
② 年用水量超过240的该市居民家庭按第三档水价交费
③ 该市居民家庭年用水量的中位数在150-180之间
④ 该市居民家庭年用水量的平均数不超过180
A. ①③ B. ①④ C.②③ D.②④
10.以下是某手机店1~4月份的两个统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
A. 4月份三星手机销售额为65万元 B. 4月份三星手机销售额比3月份有所上升
C. 4月份三星手机销售额比3月份有所下降
D. 3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
二 、填空题(本大题共8小题)
11.今年安庆市有6万名考生参加学业水平考试,为了了解这些考生的数学成绩,从中抽取1 000名考生的数学成绩进行统计分析,在这个问题中,下列说法:①每个考生是个体;②参加考试的6万名考生是总体;③1 000名考生的数学成绩是总体的一个样本;④样本容量是1 000,其中说法正确的有_____________.【来源:21cnj*y.co*m】
12.小明在纸上随手写下一串数字“1010010001”,则数字“1”出现的频率是__________.
13.今年5月份有关部门对计划去上海迪士尼乐园的部分市民的前往方式进行调查,图1和图2是收集数据后绘制的两幅不完整统计图.根据图中提供的信息,那么本次调查的对象中选择公交前往的人数是 .
14. “万人马拉松”活动组委会计划制作运动衫分发给参与者,为此,调查了部分参与者,以决定制作橙色、黄色、白色、红色四种颜色运动衫的数量.根据得到的调查数据,绘制成如图所示的扇形统计图.若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有 名.21*cnjy*com
15.在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为______人.【版权所有:21教育】
16.已知一个样本容量为60,在频数分布直方图中,各小长方形的高比为2:4:1:3,那么第二组的频数是 .
17.下面的频数分布折线图分别表示我国A市与B市在2014年4月份的日平均气温的情况,记该月A市和B市日平均气温是8℃的天数分别为a天和b天,则a+b= .
18.)根据环保局公布的广州市2013年至2014年PM 2.5的主要来源的数据,制成扇形统计图,其中所占百分比最大的主要来源是 .(填主要来源的名称)
三 、解答题(本大题共8小题,共0分)
19.某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题:
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
20.为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对概念机学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.
21.某校学生会为了解环保知识的普及情况,从该校随机抽取部分学生,对他们进行了垃圾分类了解程度的调查,根调查收集的数据绘制了如下的扇形统计图,其中对垃圾分类非常了解的学生有30人
(1)本次抽取的学生有 人;
(2)请补全扇形统计图;
(3)请估计该校1600名学生中对垃圾分类不了解的人数.
22.为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):
根据统计图中的信息,解答下列问题:
(1)求本次被调查的学生人数.
(2)将条形统计图补充完整.
(3)若该校共有1600名学生,请估计全校选择体育类的学生人数.
23.为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示.
分组
频数
4.0≤x<4.2
2
4.2≤x<4.4
3
4.4≤x<4.6
5
4.6≤x<4.8
8
4.8≤x<5.0
17
5.0≤x<5.2
5
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.
24.某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:21·世纪*教育网
(1)此次抽样调查的样本容量是______.
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?【出处:21教育名师】
25.绵阳七一中学开通了空中教育互联网在线学习平台,为了解学生使用情况,该校学生会把该平台使用情况分为A(经常使用)、B(偶尔使用)、C(不使用)三种类型,并设计了调查问卷、先后对该校初一(1)班和初一(2)班全体同学进行了问卷调查,并根据调查结果绘制成如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)求此次被调查的学生总人数;
(2)求扇形统计图中代表类型C的扇形的圆心角,并补全折线统计图;
(3)若该校初一年级学生共有1000人,试根据此次调查结果估计该校初一年级中C类型学生约有多少人.
26.某中学为了了解九年级学生体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图;
(1)这次抽样调查的样本容量是 ,并补全条形图;
(2)D等级学生人数占被调查人数的百分比为 ,在扇形统计图中C等级所对应的圆心角为 °;【来源:21·世纪·教育·网】
(3)该校九年级学生有1500人,请你估计其中A等级的学生人数.
0.浙教新版七年级下第六章数据与统计图表练习答案解析
一 、选择题
1.分析:分别根据总体、个体、样本及调查的定义逐项判断即可.
解:
某市参加中考的32000名学生的体重情况是总体,故A错误;
每名学生的体重情况是总体的一个个体,故B错误;
1500名学生的体重情况是一个样本,故C正确;
该调查属于抽样调查,故D错误;
故选C.
2.分析: 由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.21·cn·jy·com
解:A,对綦江河水质情况的调査的调查应用抽样调查,大概知道水质情况就可以了,故此选项错误,
B,对端午节期间市场粽子质量的调查适用抽样调查,利用全面调查,就不能买了,故此选项错误;
C,对某班50名同学体重情况的调査适用全面调查,人数不多,全面调查准确,故此选项正确;
D,对某类烟花爆竹燃放安全情况的调査适用抽样调查,利用全面调查,破坏性极大,就不能买了,故此选项错误.21教育网
故选C.
3.分析:根据蚕豆种子的发芽率为97.1%,可以估计黄石地区1000斤蚕豆种子中不能发芽的大约有多少,本题得以解决.2-1-c-n-j-y
解:由题意可得,
黄石地区1000斤蚕豆种子中不能发芽的大约有:1000×(1﹣97.1%)=1000×0.029=29斤,21教育名师原创作品
故选D.
.
4.分析:根据折线图的数据,分别求出相邻两个月的高清大屏手机销售额的变化值,比较即可得解.
解:8﹣9月,30﹣23=7万元,
9﹣10月,30﹣25=5万元,
10﹣11月,25﹣15=10万元,
11﹣12月,19﹣15=4万元,
所以,相邻两个月中,高清大屏手机销售额变化最大的是10﹣11月.
故选C.
5.分析:根据条形统计图可以得到哪一组的人数最多,从而可以解答本题.
解:由条形统计图可得,
人数最多的一组是4~6小时,频数为22,
故选B.
6.分析:根据扇形统计图可得参加足球的人数最少,参加乒乓球的人数最多.
解:根据题意可得:总人数=25÷25%=100(人),则参加乒乓球的人数为:100×(1-35%-25%)=40(人).
故选C
7.分析:条形统计图的特点:能清楚的表示出数量的多少;折线统计图的特点:不但可以表示出数量的多少,而且能看出各种数量的增减变化情况;扇形统计图比较清楚地反映出部分与部分、部分与整体之间的数量关系;据此进行解答即可.
解:在进行数据描述时,要显示部分在总体中所占的百分比,应采用扇形统计图; 故选:A.
8.分析:找出四组中的数字,判断出频数,即可做出判断.
解:5.5~7.5组有6,7,频数为2;7.5~9.5组有8,8,9,8,9,9,频数为6;9.5~11.5组有10,10,11,10,11,10,11,10,频数为8;11.5~13.5组有13,12,12,12,频数为4.
故选D.
9.解:年用水量不超过180的居民家庭有:0.25+0.75+1.5+1+0.5=4(万),=80%,
所以,①正确;
年用水量超过240的居民家庭有:0.15+0.15+0.05=0.35(万),=7%,故②不正确;
30-120的有2.5万人,120-330的有2.5万人,中位数应该是120,故③不正确;
由于中位数为120,用水量小于150的有3.5万人,所以该市居民家庭年用水量的平均数不超过180,④正确。
10.分析:根据销售额=总销售额×所占的百分比求出销售额,再根据有理数大小比较得出答案
解:三星手机的销售额=单月手机的总销售额×三星手机所占的百分比.根据统计图可得:三星手机三月份的销售额为:60×18%=10.8(万元),四月份三星手机的销售额为:65×17%=11.05(万元),则根据以上信息可得B是正确的.
二 、填空题
11.分析: 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解:①每个考生的数学成绩是个体,命题错误;
②参加考试的6万名考生的成绩是总体,命题错误;
③④正确.
故答案是:③④.
12.分析:首先计算数字的总数,以及1出现的频数,根据频率公式:频率=即可求解.
解:数字的总数是10,有4个1,
因而1出现的频率是:4÷10×100%=40%.
故答案是:40%.
13.分析:根据自驾车人数除以百分比,可得答案.
解:由题意,得
4800÷40%=12000,
公交12000×50%=6000,
故答案为:6000.
14.分析:根据样本中选择红色运动衫的人数占总数的百分比,据此可估计总体中选择红色运动衫的人数占总数的百分比近似相等,列式计算即可.21*cnjy*com
解:若本次活动共有12000名参与者,则估计其中选择红色运动衫的约有12000×20%=2400(名),
故答案为:2400.
15.分析:首先由第二小组有10人,占20%,可求得总人数,再根据各小组频数之和等于数据总数求得第四小组的人数,利用总人数260乘以样本中“一分钟跳绳”成绩为优秀的人数所占的比例即可求解.
解:总人数是:10÷20%=50(人),
第四小组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,
所以该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×1200=480,
故答案为:480.
16.分析:根据各小长方形的高比为2:4:1:3,得频数之比为2:4:1:3,由此即可解决问题.
解:∵样本容量为60,各小长方形的高比为2:4:1:3,
∴那么第二组的频数是60×=24,
故答案为24.
17.分析:根据折线图即可求得a、b的值,从而求得代数式的值.
解:根据图表可得:a=10,b=2, 则a+b=10+2=12. 故答案为:12.
18.分析:根据扇形统计图可得:机动车尾气所占的百分比最大,则主要来源就是机动车尾气.
解:用一个圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分在总体中所占百分比的大小,这样的统计图叫做扇形统计图.所以一看数据就知道是机动车尾气
三 、解答题
19.分析:(1)根据每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图,可以求得第一季度的汽车销售量为2100辆时,该季的汽车产量;
(2)首先判断圆圆的说法错误,然后说明原因即可解答本题.
解:(1)由题意可得,
2100÷70%=3000(辆),
即该季的汽车产量是3000辆;
(2)圆圆的说法不对,
因为百分比仅能够表示所要考查的数据在总量中所占的比例,并不能反映总量的大小.
20.分析:由阅读了6本的人数占被调查人数的30%可求得阅读6本的人数,将总人数减去阅读数是5、6、8本的人数可得阅读7本人数,据此补全条形图可得;根据样本计算出平均每人的阅读量,再用平均数乘以七年级学生总数即可得答案.
解:根据题意,阅读了6本的人数为100×30%=30(人),
阅读了7本的人数为:100﹣20﹣30﹣﹣15=35(人),
补全条形图如图:
∵平均每位学生的阅读数量为: =6.45(本),
∴估计该校七年级全体学生在2015年全年阅读中外名著的总本数为800×6.45=5160本,
答:估计该校七年级全体学生在2015年全年阅读中外名著的总本数约为5160本.
21.分析:(1)根据不了解的人数除以不了解的人数所占的百分比,可得的答案;
(2)根据有理数的减法,可得答案;
(3)根据样本估计总体,可得答案.
解:(1)30÷10%=300,
故答案为:300;
(2)如图,
了解很少的人数所占的百分比1﹣30%﹣10%﹣20%=40%,
故答案为:40%,
(3)1600×30%=480人,
该校1600名学生中对垃圾分类不了解的人数480人.
22.分析:(1)根据条形统计图和扇形统计图可知选择劳技的学生60人,占总体的30%,从而可以求得调查学生人数;
(2)根据文学的百分比和(1)中求得的学生调查数可以求得文学的有多少人,从而可以求得体育的多少人,进而可以将条形统计图补充完整;
(3)根据调查的选择体育的学生所占的百分比可以估算出全校选择体育类的学生人数.
解:(1)60÷30%=200(人),
即本次被调查的学生有200人;
(2)选择文学的学生有:200×15%=30(人),
选择体育的学生有:200﹣24﹣60﹣30﹣16=70(人),
补全的条形统计图如下图所示,
(3)1600×(人).
即全校选择体育类的学生有560人.
23.分析:(1)求出频数之和即可.
(2)根据合格率=×100%即可解决问题.
(3)从两个不同的角度分析即可,答案不唯一.
解:(1)∵频数之和=40,
∴所抽取的学生人数40人.
(2)活动前该校学生的视力达标率==37.5%.
(3)①视力4.2≤x<4.4之间活动前有6人,活动后只有3人,人数明显减少.
②活动前合格率37.5%,活动后合格率55%,
视力保健活动的效果比较好.
24.分析:(1)根据10~15吨部分的用户数和百分比进行计算;(2)先根据频数分布直方图中的数据,求得“15吨~20吨”部分的用户数,再画图,最后根据该部分的用户数计算圆心角的度数;(3)根据用水25吨以内的用户数的占比,求得该地区6万用户中用水全部享受基本价格的户数.
解:(1)∵10÷10%=100(户)
∴样本容量是100;
(2)用水15~20吨的户数:100﹣10﹣36﹣24﹣8=22(户)
∴补充图如下:
“15吨~20吨”部分的圆心角的度数=360°×=79.2°
答:扇形图中“15吨~20吨”部分的圆心角的度数为79.2°.
(3)6×=4.08(万户)
答:该地区6万用户中约有4.08万户的用水全部享受基本价格.
25.分析:(1)先由折线统计图得到偶尔使用的学生有58人,再由扇形统计图得到了解很少的学生所占的百分比,然后用58除以这个百分比即可得到接受问卷调查的学生人数;
(2)先用总数分别减去其它三组的人数得到C的学生数,再补全折线统计图;用c部分所占的百分比乘以360°即可得到c部分所对应扇形的圆心角的大小;
(3)利用样本中c程度的百分比表示该校这两项所占的百分比,然后用1000乘以这个百分比即可得到c程度的总人数的估计值.2·1·c·n·j·y
解:(1)由扇形统计图知B类型人数所占比例为58%,从折线图知B类型总人数=26+32=58人,
所以此次被调查的学生总人数=58÷58%=100人;
(2)由折线图知A人数=18+14=32人,故A的比例为32÷100=32%,
所以C类比例=1﹣58%﹣32%=10%,
所以类型C的扇形的圆心角=360°×10%=36°,
C类人数=10%×100﹣2=8人,折线图如下:
(3)根据此次可得C的比例为10%,估计该校初一年级中C类型学生约1000×10%=100人.
26.分析:(1)由A等级的人数和其所占的百分比即可求出抽样调查的样本容量;求出B等级的人数即可全条形图;
(2)用B等级的人数除以总人数即可得到其占被调查人数的百分比;求出C等级所占的百分比,即可求出C等级所对应的圆心角;
(3)由扇形统计图可知A等级所占的百分比,进而可求出九年级学生其中A等级的学生人数.
解:(1)由条形统计图和扇形统计图可知总人数=16÷32%=50人,所以B等级的人数=50﹣16﹣10﹣4=20人,
故答案为:50;
补全条形图如图所示:
(2)D等级学生人数占被调查人数的百分比=×100%=8%;
在扇形统计图中C等级所对应的圆心角=8%×360°=28.8°,
故答案为:8%,28.8;
(3)该校九年级学生有1500人,估计其中A等级的学生人数=1500×32%=480人.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
