1.4 平行线的性质 同步练习(含答案)
文档属性
| 名称 | 1.4 平行线的性质 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 372.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 15:58:49 | ||
图片预览


文档简介
1.4
平行线的性质
同步练习
一、单选题
1、下列命题正确的是( )
A、两直线与第三条直线相交,同位角相等;
B、两直线与第三条直线相交,内错角相等
C、两直线平行,内错角相等;
D、两直线平行,同旁内角相等
2、已知两个角的两边分别平行,并且这两个角的差是90°,则这两个角分别等于(
)
A.60°,150°
B.20°,110°
C.30°,120°
D.45°,135°
3、如图所示,AC平分∠BCD,且∠BCA=∠CAD=∠CAB,∠ABC=75°,
则∠BCA等于(
)
A.36°
B.35°
C.
37.5°
D.70°
4、如图,直线c与直线a、b相交,且a∥b,则下列结论:
①∠1=∠2;②∠1=∠3;③∠3=∠2中,正确的个数为(
)
A.0个
B.1个
C.2个
D.3个
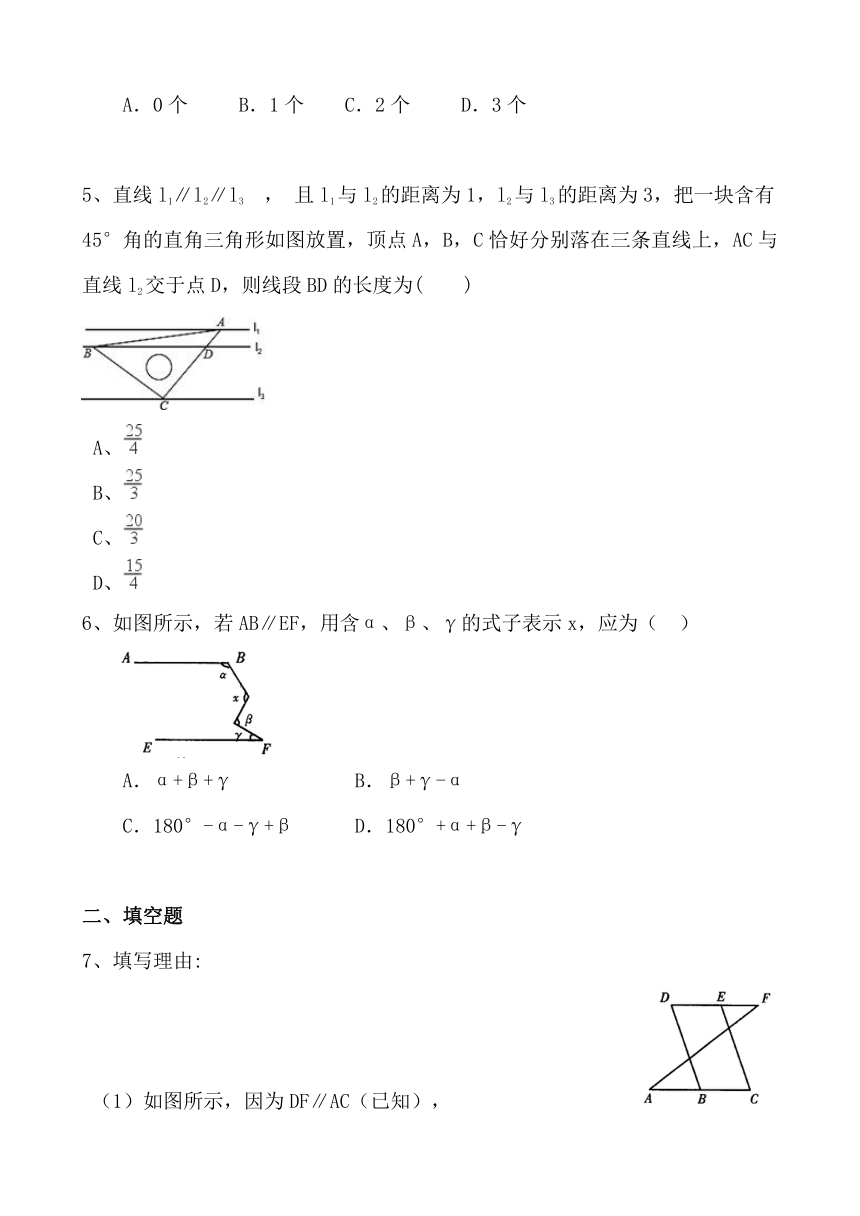
5、直线l1∥l2∥l3
,
且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A、
B、
C、
D、
6、如图所示,若AB∥EF,用含α、β、γ的式子表示x,应为(
)
A.α+β+γ
B.β+γ-α
C.180°-α-γ+β
D.180°+α+β-γ
二、填空题
7、填写理由:
(1)如图所示,因为DF∥AC(已知),
所以∠D+______=180°(__________________________)
因为∠C=∠D(已知),
所以∠C+_______=180°(_________________________)
所以DB∥EC(_________).
(2)如图所示,因为∠A=∠BDE(已知),
所以______∥_____(__________________________)
所以∠DEB=_______(_________________________)
因为∠C=90°(已知),
所以∠DEB=______(_________________________)
所以DE⊥______(_________________________)
8、如图,AB∥CD
,
以点A为圆心,小于AC长为半径作圆弧,分别交AB
,
AC于E
,
F两点,再分别以E
,
F为圆心,大于
EF长为半径作圆弧,两条圆弧交于
点P
,
作射线AP
,
交CD于点M
.
若∠ACD=114°,则∠MAB的度数为________°.
三、解答题
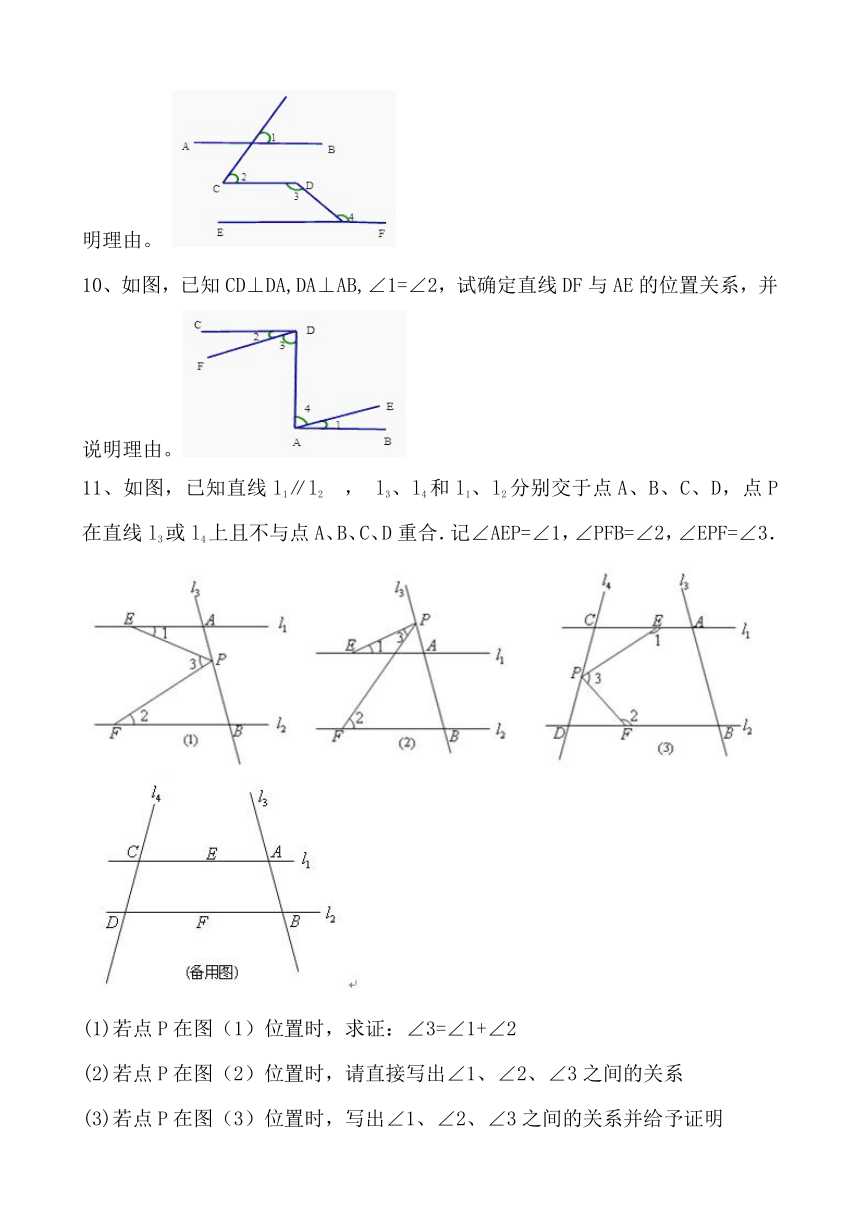
9、如图,∠1=60°,∠2=60°,∠3=100°。要使AB∥EF,∠4应为多少度?说明理由。
10、如图,已知CD⊥DA,DA⊥AB,∠1=∠2,试确定直线DF与AE的位置关系,并说明理由。
11、如图,已知直线l1∥l2
,
l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系
四、综合题
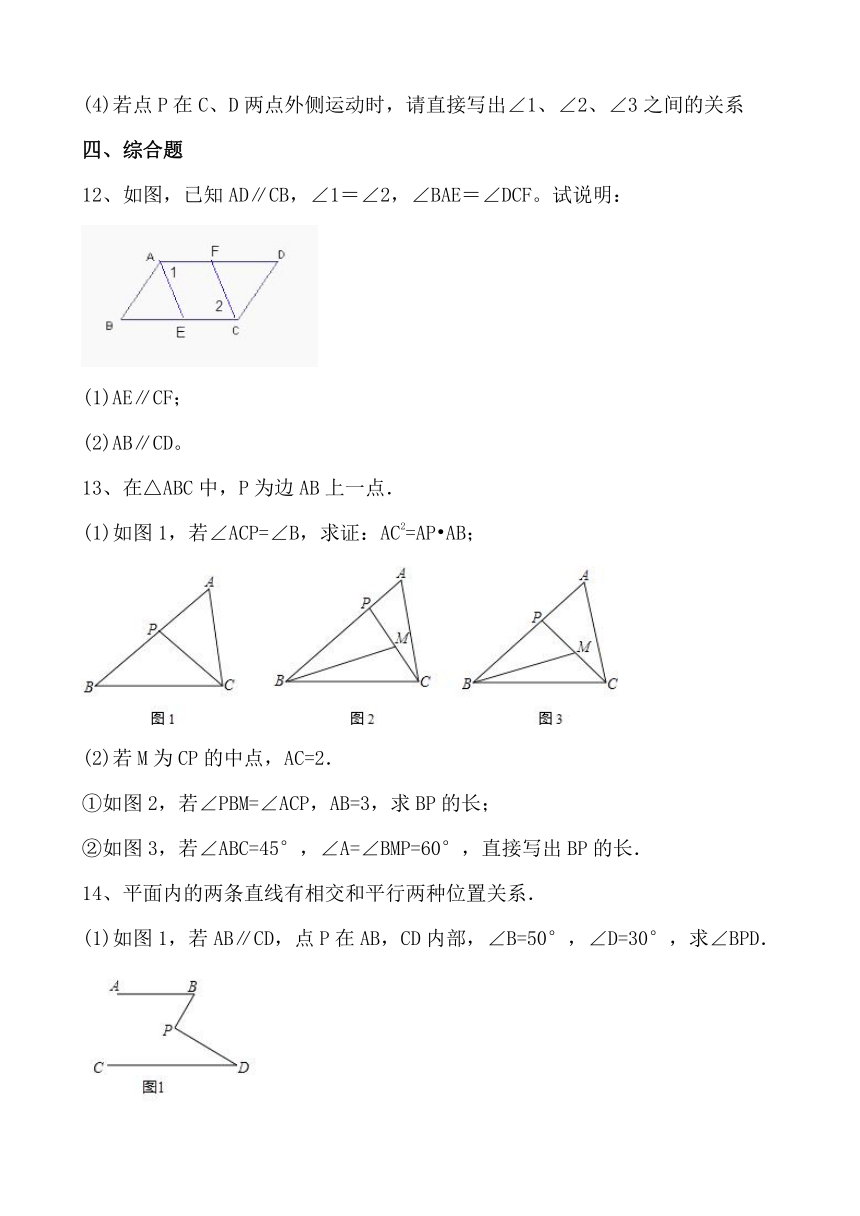
12、如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。试说明:
(1)AE∥CF;
(2)AB∥CD。
13、在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=AP AB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
14、平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB,CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB,CD外部,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论.
(3)如图3,写出∠BPD,∠B,∠D,∠BQD之间的数量关系?(不需证明)
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.
15、如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由.
16、如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
答案部分
一、单选题
1、
【答案】C
2、
【答案】
D
3、
【答案】
B
4、
【答案】D
5、
【答案】A
6、
【答案】C
二、填空题
7、【答案】(1)∠DBC
两直线平行,同旁内角互补
∠DBC
等量代换
同旁内角互补,两直线平行
(2)AC
DE
同位角相等,两直线平行
∠C
两直线平行,同位角相等
90°
等量代换
BC
垂直定义
8、
【答案】33
三、解答题
9、
【答案】100°
10、
【答案】DF∥AE
∵CD⊥DA,DA⊥AB
∴CD∥AB
∴∠CDA=∠DAB,
∵∠1=∠2
∴∠CDA-∠2=∠DAB-∠1,
即∠3=∠4
∴DF∥AE
11、
【答案】
(1)证明:过P作PQ∥l1∥l2
,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)解:
∠3=∠2﹣∠1;
证明:过P作直线PQ∥l1∥l2
,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
(3)解:
∠3=360°﹣∠1﹣∠2.
证明:过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
(4)解:
过P作PQ∥l1∥l2;
①当P在C点上方时,
同(2)可证:∠3=∠DFP﹣∠CEP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠DFP﹣∠CEP+∠2﹣∠1=0,
即∠3=∠1﹣∠2.
②当P在D点下方时,
∠3=∠2﹣∠1,解法同上.
综上可知:当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.
四、综合题
12、
【答案】
(1)(1)∵AD∥CB
(已知)
∴
∠1=∠AEB
(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴
∠AEB=
∠2(等量代换)
∴AE∥CF(同位角相等,两直线平行).
(2)∵三角形ABE的内角和是180
∴∠B+∠BAE+∠AEB=180
又∵∠AEB=
∠2(已证)
∠BAE=∠DCF(已知)
∴∠B+∠2+∠DCF=180
即∠B+∠BCD=180
∴AB∥CD(同旁内角互补,两直线平行).
13、
【答案】
(1)解:∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,
∴
,
∴AC2=AP AB;
(2)解:①取AP在中点G,连接MG,设AG=x,则PG=x,BG=3﹣x,
∵M是PC的中点,
∴MG∥AC,
∴∠BGM=∠A,
∵∠ACP=∠PBM,
∴△APC∽△GMB,
∴
,
即
,
∴x=
,
∵AB=3,
∴AP=3﹣
,
∴PB=
;
②过C作CH⊥AB于H,延长AB到E,使BE=BP,
∵∠ABC=45°,∠A=60°,
∴CH=
,HE=
+x,
∵CE2=
+9
+x)2
,
∵PB=BE,PM=CM,
∴BM∥CE,
∴∠PMB=∠PCE=60°=∠A,
∵∠E=∠E,
∴△ECP∽△EAC,
∴
,
∴CE2=EP EA,
∴3+3+x2+2
x=2x(x+
+1),
∴x=
﹣1,
∴PB=
﹣1.
14、
【答案】
(1)解:过点P作PE∥AB,
∵AB∥CD,
∴AB∥EP∥CD,
∴∠B=∠1=50°,∠D=∠2=30°,
∴∠BPD=80°
(2)解:∠B=∠BPD+∠D.
理由如下:设BP与CD相交于点O,
∵AB∥CD,
∴∠BOD=∠B,
在△POD中,∠BOD=∠BPD+∠D,
∴∠B=∠BPD+∠D
(3)解:如图,连接QP并延长,
结论:∠BPD=∠BQD+∠B+∠D
(4)解:如图,由三角形的外角性质,∠A+∠E=∠1,∠B+∠F=∠2,
∵∠1+∠2+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
15、
【答案】
(1)解:∠BPD=∠B+∠D.
理由:如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D
(2)解:如图(3):∠BPD=∠D﹣∠B.
理由:∵AB∥CD,
∴∠1=∠D,
∵∠1=∠B+∠P,
∴∠D=∠B+∠P,
即∠BPD=∠D﹣∠B;
如图(4):∠BPD=∠B﹣∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠D+∠P,
∴∠B=∠D+∠P,
即∠BPD=∠B﹣∠D.
16、
【答案】
(1)证明:如图1,
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,
∴DM=EM.
在△ADM和△NEM中,
∴
.
∴△ADM≌△NEM.
∴AM=MN.
∴M为AN的中点
(2)证明:如图2,
∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,
∴∠DAE+∠NEA=180°.
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=135°.
∵A,B,E三点在同一直线上,
∴∠ABC=180°﹣∠CBE=135°.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),
∴AD=NE.
∵AD=AB,
∴AB=NE.
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形
(3)△ACN仍为等腰直角三角形.
证明:如图3,延长AB交NE于点F,
∵AD∥NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE.
∵AD∥NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°
∴∠FBC+∠FEC=360°﹣180°=180°
∵∠FBC+∠ABC=180°
∴∠ABC=∠FEC
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
平行线的性质
同步练习
一、单选题
1、下列命题正确的是( )
A、两直线与第三条直线相交,同位角相等;
B、两直线与第三条直线相交,内错角相等
C、两直线平行,内错角相等;
D、两直线平行,同旁内角相等
2、已知两个角的两边分别平行,并且这两个角的差是90°,则这两个角分别等于(
)
A.60°,150°
B.20°,110°
C.30°,120°
D.45°,135°
3、如图所示,AC平分∠BCD,且∠BCA=∠CAD=∠CAB,∠ABC=75°,
则∠BCA等于(
)
A.36°
B.35°
C.
37.5°
D.70°
4、如图,直线c与直线a、b相交,且a∥b,则下列结论:
①∠1=∠2;②∠1=∠3;③∠3=∠2中,正确的个数为(
)
A.0个
B.1个
C.2个
D.3个
5、直线l1∥l2∥l3
,
且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( )
A、
B、
C、
D、
6、如图所示,若AB∥EF,用含α、β、γ的式子表示x,应为(
)
A.α+β+γ
B.β+γ-α
C.180°-α-γ+β
D.180°+α+β-γ
二、填空题
7、填写理由:
(1)如图所示,因为DF∥AC(已知),
所以∠D+______=180°(__________________________)
因为∠C=∠D(已知),
所以∠C+_______=180°(_________________________)
所以DB∥EC(_________).
(2)如图所示,因为∠A=∠BDE(已知),
所以______∥_____(__________________________)
所以∠DEB=_______(_________________________)
因为∠C=90°(已知),
所以∠DEB=______(_________________________)
所以DE⊥______(_________________________)
8、如图,AB∥CD
,
以点A为圆心,小于AC长为半径作圆弧,分别交AB
,
AC于E
,
F两点,再分别以E
,
F为圆心,大于
EF长为半径作圆弧,两条圆弧交于
点P
,
作射线AP
,
交CD于点M
.
若∠ACD=114°,则∠MAB的度数为________°.
三、解答题
9、如图,∠1=60°,∠2=60°,∠3=100°。要使AB∥EF,∠4应为多少度?说明理由。
10、如图,已知CD⊥DA,DA⊥AB,∠1=∠2,试确定直线DF与AE的位置关系,并说明理由。
11、如图,已知直线l1∥l2
,
l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明
(4)若点P在C、D两点外侧运动时,请直接写出∠1、∠2、∠3之间的关系
四、综合题
12、如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。试说明:
(1)AE∥CF;
(2)AB∥CD。
13、在△ABC中,P为边AB上一点.
(1)如图1,若∠ACP=∠B,求证:AC2=AP AB;
(2)若M为CP的中点,AC=2.
①如图2,若∠PBM=∠ACP,AB=3,求BP的长;
②如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
14、平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若AB∥CD,点P在AB,CD内部,∠B=50°,∠D=30°,求∠BPD.
(2)如图2,将点P移到AB,CD外部,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论.
(3)如图3,写出∠BPD,∠B,∠D,∠BQD之间的数量关系?(不需证明)
(4)如图4,求出∠A+∠B+∠C+∠D+∠E+∠F的度数.
15、如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由.
16、如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
答案部分
一、单选题
1、
【答案】C
2、
【答案】
D
3、
【答案】
B
4、
【答案】D
5、
【答案】A
6、
【答案】C
二、填空题
7、【答案】(1)∠DBC
两直线平行,同旁内角互补
∠DBC
等量代换
同旁内角互补,两直线平行
(2)AC
DE
同位角相等,两直线平行
∠C
两直线平行,同位角相等
90°
等量代换
BC
垂直定义
8、
【答案】33
三、解答题
9、
【答案】100°
10、
【答案】DF∥AE
∵CD⊥DA,DA⊥AB
∴CD∥AB
∴∠CDA=∠DAB,
∵∠1=∠2
∴∠CDA-∠2=∠DAB-∠1,
即∠3=∠4
∴DF∥AE
11、
【答案】
(1)证明:过P作PQ∥l1∥l2
,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)解:
∠3=∠2﹣∠1;
证明:过P作直线PQ∥l1∥l2
,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
(3)解:
∠3=360°﹣∠1﹣∠2.
证明:过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
(4)解:
过P作PQ∥l1∥l2;
①当P在C点上方时,
同(2)可证:∠3=∠DFP﹣∠CEP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠DFP﹣∠CEP+∠2﹣∠1=0,
即∠3=∠1﹣∠2.
②当P在D点下方时,
∠3=∠2﹣∠1,解法同上.
综上可知:当P在C点上方时,∠3=∠1﹣∠2,当P在D点下方时,∠3=∠2﹣∠1.
四、综合题
12、
【答案】
(1)(1)∵AD∥CB
(已知)
∴
∠1=∠AEB
(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴
∠AEB=
∠2(等量代换)
∴AE∥CF(同位角相等,两直线平行).
(2)∵三角形ABE的内角和是180
∴∠B+∠BAE+∠AEB=180
又∵∠AEB=
∠2(已证)
∠BAE=∠DCF(已知)
∴∠B+∠2+∠DCF=180
即∠B+∠BCD=180
∴AB∥CD(同旁内角互补,两直线平行).
13、
【答案】
(1)解:∵∠ACP=∠B,∠A=∠A,
∴△ACP∽△ABC,
∴
,
∴AC2=AP AB;
(2)解:①取AP在中点G,连接MG,设AG=x,则PG=x,BG=3﹣x,
∵M是PC的中点,
∴MG∥AC,
∴∠BGM=∠A,
∵∠ACP=∠PBM,
∴△APC∽△GMB,
∴
,
即
,
∴x=
,
∵AB=3,
∴AP=3﹣
,
∴PB=
;
②过C作CH⊥AB于H,延长AB到E,使BE=BP,
∵∠ABC=45°,∠A=60°,
∴CH=
,HE=
+x,
∵CE2=
+9
+x)2
,
∵PB=BE,PM=CM,
∴BM∥CE,
∴∠PMB=∠PCE=60°=∠A,
∵∠E=∠E,
∴△ECP∽△EAC,
∴
,
∴CE2=EP EA,
∴3+3+x2+2
x=2x(x+
+1),
∴x=
﹣1,
∴PB=
﹣1.
14、
【答案】
(1)解:过点P作PE∥AB,
∵AB∥CD,
∴AB∥EP∥CD,
∴∠B=∠1=50°,∠D=∠2=30°,
∴∠BPD=80°
(2)解:∠B=∠BPD+∠D.
理由如下:设BP与CD相交于点O,
∵AB∥CD,
∴∠BOD=∠B,
在△POD中,∠BOD=∠BPD+∠D,
∴∠B=∠BPD+∠D
(3)解:如图,连接QP并延长,
结论:∠BPD=∠BQD+∠B+∠D
(4)解:如图,由三角形的外角性质,∠A+∠E=∠1,∠B+∠F=∠2,
∵∠1+∠2+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
15、
【答案】
(1)解:∠BPD=∠B+∠D.
理由:如图2,过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∴∠BPD=∠1+∠2=∠B+∠D
(2)解:如图(3):∠BPD=∠D﹣∠B.
理由:∵AB∥CD,
∴∠1=∠D,
∵∠1=∠B+∠P,
∴∠D=∠B+∠P,
即∠BPD=∠D﹣∠B;
如图(4):∠BPD=∠B﹣∠D.
理由:∵AB∥CD,
∴∠1=∠B,
∵∠1=∠D+∠P,
∴∠B=∠D+∠P,
即∠BPD=∠B﹣∠D.
16、
【答案】
(1)证明:如图1,
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为DE的中点,
∴DM=EM.
在△ADM和△NEM中,
∴
.
∴△ADM≌△NEM.
∴AM=MN.
∴M为AN的中点
(2)证明:如图2,
∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,
∴∠DAE+∠NEA=180°.
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=135°.
∵A,B,E三点在同一直线上,
∴∠ABC=180°﹣∠CBE=135°.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),
∴AD=NE.
∵AD=AB,
∴AB=NE.
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形
(3)△ACN仍为等腰直角三角形.
证明:如图3,延长AB交NE于点F,
∵AD∥NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE.
∵AD∥NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°
∴∠FBC+∠FEC=360°﹣180°=180°
∵∠FBC+∠ABC=180°
∴∠ABC=∠FEC
在△ABC和△NEC中,
∴△ABC≌△NEC.
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
