2.3解二元一次方程组 课件

课件31张PPT。解二元一次方程组 温故而知新1、用含x的代数式表示y ：
(1) x + y = 22
(2)5 x =2 y
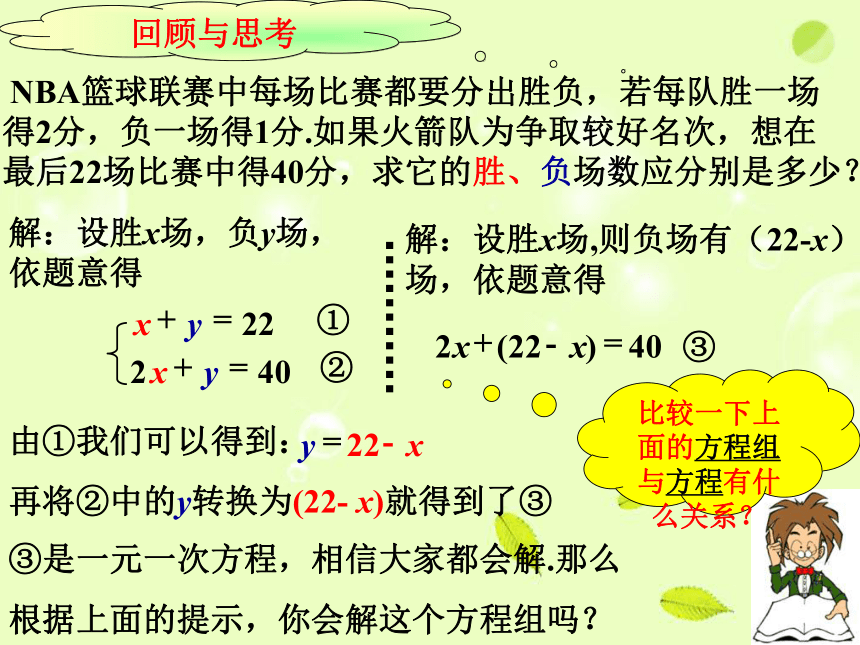
(3)2 x - y =52、用含y 的代数式表示x ：2 x - 7 y = 8y= 22- x y = 2 x -5回顾与思考 NBA篮球联赛中每场比赛都要分出胜负，若每队胜一场得2分，负一场得1分.如果火箭队为争取较好名次，想在最后22场比赛中得40分，求它的胜、负场数应分别是多少？解：设胜x场，负y场，依题意得③是一元一次方程，相信大家都会解.那么
根据上面的提示，你会解这个方程组吗？再将②中的y转换为(22- x)就得到了③解：设胜x场,则负场有（22-x）场，依题意得比较一下上面的方程组与方程有什么关系？ 二元一次方程组中有两个未知数，
如果消去其中一个未知数，将二元一次方
程组转化为我们熟悉的一元一次方程，我
们就可以先解出一个未知数，然后再设法
求另一个未知数.这种将未知数的个数由多
化少、逐一解决的思想，叫做消元思想.请同学们读一读：代入消元法二元一次方程组代入消元法转化一元一次方程解方程组：解：①②由 ①得：y = 12 –x.③把③代入②得：2x +12-x= 20.解这个一元一次方程，得
x = 5.把x =8代入③，得y =4.所以原方程组的解是x = 8，y = 4.解 把②代入①，得2y-3（y-1）=1，
即2y-3y+3=1，解得y=2.
把y=2代入②，得x=2-1=1.
所以原方程组的解是
例1 解方程组
①
②解 由①，得2x=8+7y，即
把③代入②，得
∴ 解得
把 代入③，得
所以原方程组的解是分析 利用其中一个方程．将一个未知数用关于另一个未知数的代数式表示，就可以用代入法解这个方程组．将其中一个方程的一个未知数用另一个未知数表示时．通常我们选择使运算比较简便的方程．例2 解方程组 ①
②③1、将方程组里的一个方程变形，用含有一个未知数的式子表示另一个未知数；2、用这个式子代替另一个方程中相应的未知数，得到一个一元一次方程，求得一个未知数的值；3、把这个未知数的值代入上面的式子，求得另一个未知数的值；4、写出方程组的解.变代求写说说方法:1、解方程组：解：①②由 ①得：y = 7 –x.③把③代入②得：3x +7-x= 17.解得 x = 5.把x =5代入③，得y =2.∴x = 5,y = 2.2、 解方程组解：①②由 ①得：x = 4+ y.③把③代入②得：3(4+ y) -8y-10= 0.解得 y = -0.8.把y = -0.8代入③，得x =4+ ×(-0.8)，
即 x=1.2.∴x = 1.2,y = -0.8.解：（在实践中学习探究）由② ，得 x=13 - 4y ③ 把③代入① ，得
2（13 - 4y）+3y=16 26 –8y +3y =16 -5y= -10 y=2把y=2代入③ ，得 x=5把③代入②可以吗？试试看把y=2代入① 或②可以吗？把求出的解代入原方程组，可以检验你得到的解对不对.　随堂练习：⑴ 用代入消元法解下列方程组：（1）（2）用代入法解二元一次方程组：（3）（4）1、二元一次方程组代入消元法一元一次方程2、代入消元法的一般步骤：3、思想方法：转化思想、消元思想、
方程（组）思想.变代求写转化合并同类项(1) 3x+(-3x) =_____(2) 2y-2y=______(3) 9x+_____=0(4) 7y-_____=0想一想：在一个方程组里，如果某个未知数的系数是相同或互为相反数，我们可不可以用加减法消去这个未知数.00(-9x)7y做一做:解下面的二元一次方程组标准的代入消元法②①还有别的方法吗？ 认真观察此方程组中各个未知数
的系数有什么特点，并分组讨论看
还有没有其它的解法，并尝试一下能
否求出它的解.新思路 新体验①②分析： 3x+5y +2x － 5y＝10 ①左边 + ② 左边 = ① 右边 + ②右边5x ＝10
x=2（3x ＋ 5y）+（2x － 5y）＝ 21 + (－11)等式性质②①①②① + ②① － ②思考联系上面的解法，想一想怎样解方程组
例3 解方程组①
②解：①-②得9t=3，解得t=
把t= 代入①（代入②可以吗？）得
解得s=
所以原方程组的解是解 ①×3，得9x-6y=33． ③
②×2．得 4x+6y=32． ④
③+④．得13x=65，
∴x=5.
把x=5代入①，得3×5-2y=11，
解得y=2.
所以原方程组的解是例4 解方程组①
②分析 先通过方程的变形．使得某个未知数的系数的绝对值相同就可以把两个方程的两边相加或相减来消元．感悟规律 揭示本质 两个二元一次方程中同一未知数的系数相反或相等时，将两个方程的两边分别相加或相减，就能消去这个未知数，得到一个一元一次方程，这种方法叫做加减消元法，简称加减法.
2x-5y=7 ①
2x+3y=-1 ② 观察方程组中的两个方程，未知数x的系数相等，都是2.把两个方程两边分别相减，就可以消去未知数x，同样得到一个一元一次方程.分析：举一反三解方程组解：把 ②－①得: 8y＝－8
y＝－1把y ＝－1代入①，得：
2x－5×（－1）＝7解得:x＝1举一反三解方程组：①
②解：①+②，得7y＝14,即，x＝2.把x＝2代人①，得6+7y=9.解得所以运用新知 拓展创新分析：1、要想用加减法解二元一次方程组
必须具备什么条件？2、此方程组能否直接用加减法消元？ 用加减法解方程组:解：
①×3得 6x+9y=36 ③所以原方程组的解是③－④得: y=2把y ＝2代入①，
解得: x＝3②×2得 6x+8y=34 ④用加减法先消去未知数y该如何解？解得的结果与左面的解相同吗？基本思路:主要步骤：加减消元:加减消元法解方程组基本思路是什么？主要步骤有哪些？某车间有90名工人，每人每天平均能生产螺栓15个或螺帽24个，要使一个螺栓配套两个螺帽，应如何分配工人才能使螺栓和螺帽刚好配套？设生产螺栓x人，生产螺帽y人，列方程组为（ ）
A、 B、


C、 D、C练一练：1、两种枕木共300根，甲种枕木的总重量比乙种枕木的总重量轻1吨，如果每根枕木甲种重46千克，乙种重28千克，两种枕木各多少根？
2、蔬菜批发站有一批青菜分给两个学校的食堂，甲校食堂分得的5倍比乙校食堂分得的6倍少10kg；甲校食堂分得的3倍与乙校食堂分得的2倍的和是470kg.甲、乙两校食堂各分得青菜多少？