2.2二元一次方程组 课件

课件34张PPT。解二元一次方程组1、指出 三对数值分别是下面哪一个方程组的解.① ② ③解：①（ ）是方程组（ ）的解；②（ ）是方程组（ ）的解；③（ ）是方程组（ ）的解；上一节我们学习了二元一次方程及有关知识，现在大家先完成下面各题：-3802　　宋集中学现有校舍6000m2，现计划征用一片空地修建一座新校舍，使校舍总面积增加20%.若建造新校舍的面积为征用空地面积的4倍，那么需征用多少空地，建造多少新校舍？（单位为m2）　①
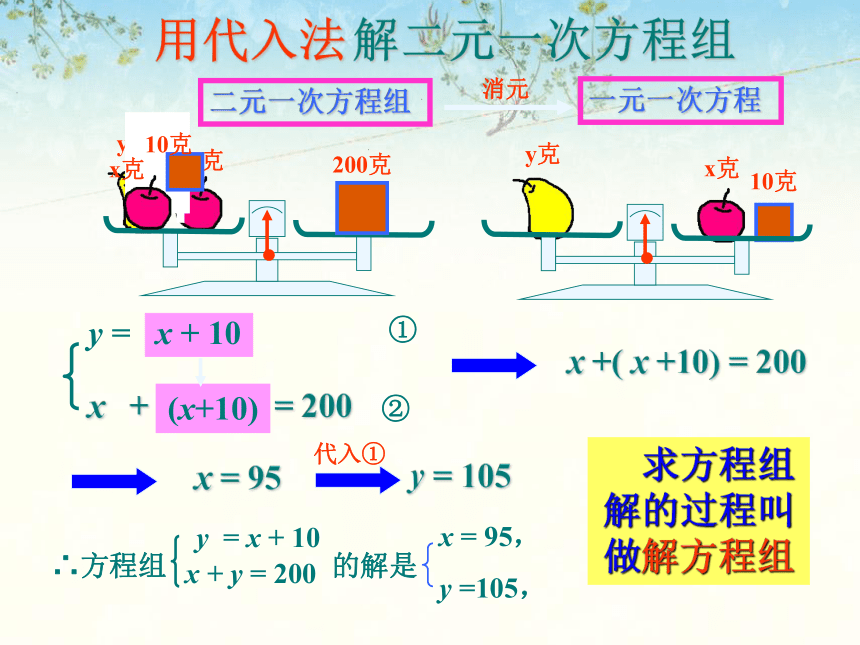
　②　　分析：如果设应征用的空地为xm2，建造新校舍ym2，那么根据题意可列出方程组：如何求出这个方程组的解呢？ x + y = 200y = x + 10解二元一次方程组一元一次方程二元一次方程组消元用代入法x克10克(x+10)x +( x +10) = 200①②x = 95代入①y = 105 求方程组解的过程叫做解方程组解方程组解：①②把②代入①得:4x–x = 6000×20%3x = 1200x = 400把x=400代入②，得:y= 4x= 4×400= 1600∴x = 400y = 1600y –x= 6000×20%y = 4x解方程组解：①②把②代入①得:4x–x = 6000×20%3x = 1200x = 400把x=400代入②，得:y= 4x= 4×400= 1600∴x = 400y = 1600练 习 题 解方程组解 把②代入①，得2y-3（y-1）=1，
即2y-3y+3=1，解得y=2.
把y=2代入②，得x=2-1=1.
所以原方程组的解是
例1 解方程组
①
②解 由①，得2x=8+7y，即
把③代入②，得
∴ 解得
把 代入③，得
所以原方程组的解是分析 利用其中一个方程．将一个未知数用关于另一个未知数的代数式表示，就可以用代入法解这个方程组．将其中一个方程的一个未知数用另一个未知数表示时．通常我们选择使运算比较简便的方程．例2 解方程组 ①
②③解方程组：解：①②由 ①得：y = 12 –x.③把③代入②得：2x +12-x= 20.解这个一元一次方程，得
x = 5.把x =8代入③，得y =4.所以原方程组的解是x = 8，y = 4.解方程组：解：①②由 ①得：y = 7 –x.③把③代入②得：3x +7-x= 17.解得 x = 5.把x =5代入③，得y =2.∴x = 5，y = 2.2、 解方程组解：①②由 ①得：x = 4+ y.③把③代入②得：3(4+ y) -8y-10= 0.解得 y = -0.8.把y = -0.8代入③，得x =4+ ×(-0.8)，
即 x=1.2.∴x = 1.2，y = -0.8.练 习 题 解方程组3 解方程组①
②把两个方程的两边分别相减，就消去了x，得到9y＝-18，即，y＝-2.把y＝-2代人①，得3x+5×（-2)=5.解得 x=5.这样，我们求得了一对x、y的值．显然
原方程组的解．思 考
请你概括一下上面解法的思路，并想想，怎样解方程组：上面的解法，是由二元一次方程组中一个方程，将一个未知数用含另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解，这种方法叫代入消元法，简称代入法.归 纳想一想，怎样解下面的二元一次方程组呢？2x-5y=7 ①
2x+3y=-1 ②分析：观察方程组中的两个方程，未知数x的系数相等，都是2，把这两个方程两边分别相减，就可以消去未知数x，同样得到一个一元一次方程.怎样解下面的二元一次方程组呢？①②把②变形得：代入①，不就消去x了！小彬把②变形得可以直接代入①呀！小明（3x＋5y）+（2x－5y）＝ 21 + (－11)3x+5y = 21
2x－5y = -11按小丽的思路，你能消去
一个未知数吗？小丽分析： ①左边 + ②左边 = ①右边 + ②右边把x＝2代入①，得y＝3， 的解是所以x＝23x+5y+2x－5y＝10 5x+0y＝10
5x＝10 参考小丽的思路，怎样解下面的二元一次方程组呢？分析：观察方程组中的两个方程，未知数x的系数相等，即都是2．所以把这两个方程两边分别相减，就可以消去未知数x，得到一个一元一次方程．解：由 ②-①得：8y=-8
y=-1
把y =-1代入①，得
2x-5×（-1）=7
解得：x=1所以原方程组的解是例3 解方程组①
②解：①-②得9t=3，解得t=
把t= 代入①（代入②可以吗？）得
解得s=
所以原方程组的解是解 ①×3，得9x-6y=33． ③
②×2．得 4x+6y=32． ④
③+④．得13x=65，
∴x=5.
把x=5代入①，得3×5-2y=11，
解得y=2.
所以原方程组的解是例4 解方程组①
②分析 先通过方程的变形．使得某个未知数的系数的绝对值相同就可以把两个方程的两边相加或相减来消元．解方程组：①
②解：由①+②，得4x＝6，把 代入①，得所以原方程的解是解方程组：①
②解：①×3，得15x-6y＝12.③-④，得所以原方程的解是③②×2，得4x-6y＝-10.④11x=22.x=2.将x=2代入①，得5×2-2y＝4.y＝3.上面这些方程组的特点是什么？
解这类方程组的基本思路是什么？主要步骤有哪些？主要步骤： 特点：基本思路：写解求解加减二元一元.加减消元：消去一个元；分别求出两个未知数的值；写出原方程组的解.同一个未知数的系数相同或互为相反数.解方程组：①
②解：①+②，得7y＝14，即，x＝2.把x＝2代人①，得6+7y=9.解得所以用加减法解方程组：当方程组中两方程不具备上述特点时，必须用等式性质来改变方程组中方程的形式，即得到与原方程组同解的且某未知数系数的绝对值相等的新的方程组，从而为加减消元法解方程组创造条件． ①×3得：所以原方程组的解是①②分析： ③-④得： y=2，把y＝2代入①，
解得： x＝3， ②×2得：6x+9y=36 ③6x+8y=34 ④注意：1.解二元一次方程组的基本思路是消元.
2.消元的方法有：代入消元和加减消元.
3.解二元一次方程组的一般步骤：消元、求解、写解.解方程组：①
②解：①×3，②×2，得19x＝114，设法把这个方程组变成像例3或例4那样的形式．想想看，如何才能达到要求？③
④③+④，得即 x=6.把x=6代入②，得所以30+6y=42解得 y=2巩固提高 练一练，相信你能行 某中学七年级（3）班51名同学为“希望工程”捐款，共捐款181元，捐款情况如下表，表格中捐款3元和4元的人数不小心被墨水污染已看不清楚．
设捐款3元的有x名同学，捐款4元的有y名同学，根据题意，可列方程组为：