浙教版七年级下 3.1.1同底数幂的乘法 课件
文档属性
| 名称 | 浙教版七年级下 3.1.1同底数幂的乘法 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-05 00:00:00 | ||
图片预览





文档简介
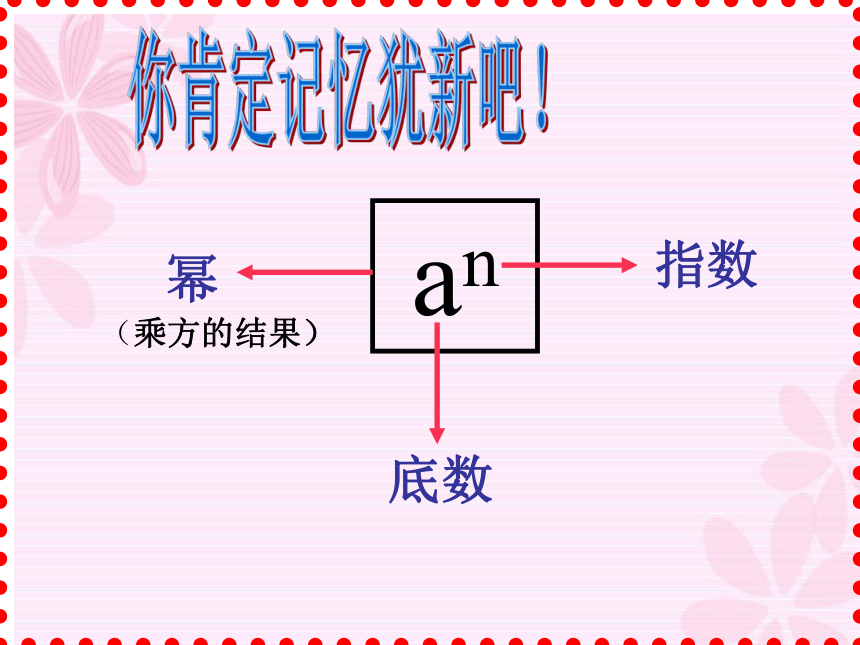
课件18张PPT。同底数幂的乘法一1.什么叫乘方?求几个相同因数的积的运算叫做乘方。(1)、 2×2 ×2 = 2( )3(2)、 a·a·a·a·a = a( ) 5(3)、 x4=x· x· x· xan(乘方的结果)你肯定记忆犹新吧!思考:观察上面各题左右两边,底数、指数有什么关系?
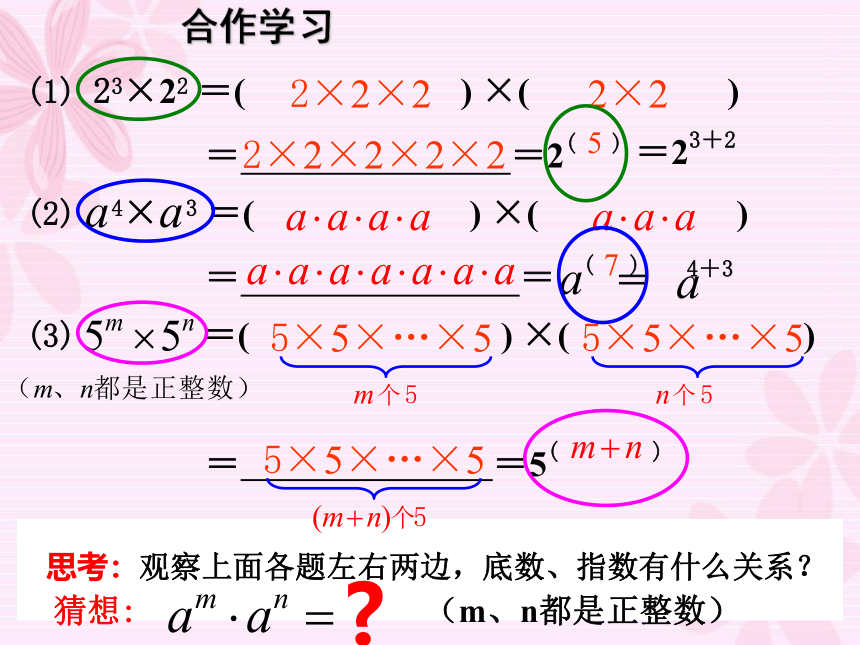
(1) 23×22 =( ) ×( )
= =2( )(2) 4× 3 =( ) ×( )
= = ( )(3) =( ) ×( )
= =5( )=23+22×2×22×22×2×2×2×2575×5×…×55×5×…×55×5×…×5合作学习猜想: am · an= (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a(aa…a)(aa…a)am+n(乘方的意义)(乘法结合律)(乘方的意义)am · an = am+n (m、n都是正整数)同底数幂相乘,底数 ,指数 。不变相加 同底数幂的乘法法则: 注意:条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加am · an · ap 等于什么?想一想:猜想:? 火眼金睛 ? 1.下列计算对吗?如果不对,应怎样改正?×××××(6)a2·a3- a3·a2 = 0 √例1 计算下列各式,结果用幂的形式表示
(1) 7 8 × 7 3
=78+3 =711 am · an = am+n (m、n都是正整数)例1 计算下列各式,结果用幂的形式表示
(3) (-2) 8 × (-2)7
=(-2)8+7 =(-2)15=-215 am · an = am+n (m、n都是正整数)
(2) (-2) 8 × (-2)6
=(-2)8+6 =(-2)14=214例1 计算下列各式,结果用幂的形式表示
(-2) 8 × 27
=28+7 =215 am · an = am+n (m、n都是正整数)
=2 8 × 27
变式一:变式二:
(-2) 7 × 28
= -2 7 × 28
= -28+7 = - 215例1 计算下列各式,结果用幂的形式表示
-2 8 × (-2)3
am · an = am+n (m、n都是正整数)=28+3 = -28× (-23 )=211 = 28× 23 变式三:= -28× (-23 )
+ 211
= 2 × 211 =212 例1 计算下列各式,结果用幂的形式表示
(5)(a-b)2 (a-b)
=(a-b)2+1 =(a-b)31 am · an = am+n (m、n都是正整数)变式 :
(b-a)2 (a-b)
=(a-b)2 (a-b)
=(a-b)2+1 =(a-b)3变式 :
同底数幂相乘时,指数是相加的;
底数为负数时,先用同底数幂的乘法法则计算,最后确定结果的正负;
不能疏忽指数为1的情况;
公式中的a可为一个有理数、单项式或多项式(整体思想)易错题(1)
(2)
(3)
(4)
(5)(6)
(7)
(8)
(9)
(10)2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×=3.拓展与延伸(1)计算:x×x2×x3×x4 x100
(2)如果x m-n ×x 2n+1=x 11,
且y m-1×y 4-n=y 7,求m,n的值.
3、-(x-y)2k·(y-x)2k+1=(x-y)9 (k为正整数),求k的值
4、计算(-2)2004 +(-2)2005同底数幂的乘法性质:幂的意义:课堂聚焦
(1) 23×22 =( ) ×( )
= =2( )(2) 4× 3 =( ) ×( )
= = ( )(3) =( ) ×( )
= =5( )=23+22×2×22×22×2×2×2×2575×5×…×55×5×…×55×5×…×5合作学习猜想: am · an= (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a(aa…a)(aa…a)am+n(乘方的意义)(乘法结合律)(乘方的意义)am · an = am+n (m、n都是正整数)同底数幂相乘,底数 ,指数 。不变相加 同底数幂的乘法法则: 注意:条件:①乘法 ②同底数幂
结果:①底数不变 ②指数相加am · an · ap 等于什么?想一想:猜想:? 火眼金睛 ? 1.下列计算对吗?如果不对,应怎样改正?×××××(6)a2·a3- a3·a2 = 0 √例1 计算下列各式,结果用幂的形式表示
(1) 7 8 × 7 3
=78+3 =711 am · an = am+n (m、n都是正整数)例1 计算下列各式,结果用幂的形式表示
(3) (-2) 8 × (-2)7
=(-2)8+7 =(-2)15=-215 am · an = am+n (m、n都是正整数)
(2) (-2) 8 × (-2)6
=(-2)8+6 =(-2)14=214例1 计算下列各式,结果用幂的形式表示
(-2) 8 × 27
=28+7 =215 am · an = am+n (m、n都是正整数)
=2 8 × 27
变式一:变式二:
(-2) 7 × 28
= -2 7 × 28
= -28+7 = - 215例1 计算下列各式,结果用幂的形式表示
-2 8 × (-2)3
am · an = am+n (m、n都是正整数)=28+3 = -28× (-23 )=211 = 28× 23 变式三:= -28× (-23 )
+ 211
= 2 × 211 =212 例1 计算下列各式,结果用幂的形式表示
(5)(a-b)2 (a-b)
=(a-b)2+1 =(a-b)31 am · an = am+n (m、n都是正整数)变式 :
(b-a)2 (a-b)
=(a-b)2 (a-b)
=(a-b)2+1 =(a-b)3变式 :
同底数幂相乘时,指数是相加的;
底数为负数时,先用同底数幂的乘法法则计算,最后确定结果的正负;
不能疏忽指数为1的情况;
公式中的a可为一个有理数、单项式或多项式(整体思想)易错题(1)
(2)
(3)
(4)
(5)(6)
(7)
(8)
(9)
(10)2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .35623 23 3253622 × = 33 32 × ×=3.拓展与延伸(1)计算:x×x2×x3×x4 x100
(2)如果x m-n ×x 2n+1=x 11,
且y m-1×y 4-n=y 7,求m,n的值.
3、-(x-y)2k·(y-x)2k+1=(x-y)9 (k为正整数),求k的值
4、计算(-2)2004 +(-2)2005同底数幂的乘法性质:幂的意义:课堂聚焦
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
